Esta página recoge el estado de un artículo en desarrollo sobre este importante tema de la Lacería
Método y proyecto: Empezar por el final:
Resultados más interesantes o importantes:
Exponerlos en unas conclusiones
Retroceder y demostrarlo
Retroceder e introducirlo en su contexto.
Resumen
Bibliografía
Redes en la lacería II
Francisco Javier Sánchez González [1]
Palabras clave (para buscar información en Internet y en bibliotecas):
Lacería, lazo, decoración islámica, carpintería de lo blanco, geometría, grupos de simetrías, Islamic Arabesque, arabesco, lacería, lazo, decoración entrelazada.Índice
Resumen
Introducción
Redes y orden
Ángulos e intersecciones
Simetría y giros
Reflejo y simetría axial
Distancias, separaciones y orden
Generación de una red mediante partes de ella
Elemento Generador de Red
Bloque de Desplazamiento de Red
Periodicidad
Valores de las separaciones en la red periódica y simétrica
Secuencias de separaciones
Secuencias simétricas
Descentrado
Diseño general de redes periódicas
Redes periódicas de 8
Distancia y ángulos en redes periódicas de 12 (‘)
Puntos de reflejo.
Catálogo de redes de 8
Red interna al EG y general. Reflejo y prolongación.
Redes periódicas en general
Condiciones
Conclusiones
Bibliografía
Abstract. The geometric interlaced decoration is always inlaid over a not always evident rectilinear lattice. But only the comprehension of it allows the complete understanding of the traditional designs and their harmonic developments in new others. This paper introduces a simple and robust method to design the the well-known lattices and a virtually infinite number of periodic and symmetric new ones, the only ones really interesting in this beautiful style, which appeared in Islamic, Jewish and Christian cultures, especially in the first one. Thus the maintenance and restoration of decayed or damaged panels is also facilitated in a correct and sensitive way.
Introducción
Los diseños de lacería aparecen en situaciones y materiales muy diversos. Así lo hacen en la estructura y revestimiento de techos y artesonados en las artes andalusí, mudéjar y judía en nuestro país, ligados a las religiones musulmana, cristiana y hebrea (). Pero también aparecen en todo el territorio tocado por la extensión del Islam, desde Marruecos a la India, especialmente Egipto, Turquía, Irán, en muy diferentes épocas y civilizaciones. Cada pueblo en esta zona aportó su particular idiosincrasia a esta decoración común, y le impregnó de elementos autónomos. Por ejemplo, los turcos, que poseen intrincados diseños milenarios, encontrados en sellos y dibujos, aportan una cierta dureza a su lacería, muy variada. Los persas lirismo y fantasía.
Los materiales son también diversos: madera, bien estructural o decorativa en techumbres, puertas y contraventanas, celosías y artesonados; azulejo y alicatado en revestimientos horizontales y verticales; estuco en igual situación; ladrillo, en techos, suelos y cúpulas; en jardines los macizos de plantas; y dibujos o diseños en libros, manuscritos y tejidos.
Toda esta variedad responde a una profunda unidad: la de las redes geométricas de familias de rectas paralelas en un número entero de direcciones en el plano. A dilucidar esta unidad, tanto en su aspecto teórico como en el de comprender mejor los diseños de lazo existentes y generar otros nuevos, se dirige este escrito.
De modo que adoptaremos un acercamiento sistemático y general, que se centra en la base geométrica, inmutable, que subyace en todas las apariciones de diseños diferentes en materiales y situaciones diversas. Este acercamiento fundamenta y complementa los muy útiles y necesarios estudios con otras orientaciones más historicistas, arqueológicas u orientadas a la construcción.
Hay una utilidad adicional. Cuando falta esta referencia geométrica los dibujos y esquemas modernos carecen de precisión. Y el caso es aún mayor cuando estos diseños defectuosos se llevan a cabo en la propia realidad, como ocurre en restauraciones de monumentos antiguos, imitando en ocasiones el diseño sin comprenderlo, lo que lleva a errores que estropean el trabajo y el resultado y menoscaban su belleza.
En conclusión, parece haberse perdido en ocasiones el secreto de los diseños, ese secreto, por otra parte simple y sistemático, que parecen haber poseído bien los antiguos, a juzgar por la belleza y perfección de su obra. Continuemos y generalicemos ese conocimiento y arte con los que trabajaron.
Enlazamos así con el significado de alarife, de al-‘aref, el que sabe, el que conoce, el que está al tanto de los significados ocultos de las cosas (‘aref es el tipo de derviche esotérico en la tradición persa, mientras que el sufí sería el de acercamiento más devociónal, ortodoxo y de escuela). De modo que el alarife poseería un saber más general que el que sólo sabe hacer.
Redes y orden
La complejidad, a veces grande, de los diseños de lacería enmascara con frecuencia la presencia de esa red subyacente. Pero en todos podemos percibir varias direcciones en el plano a las que los diferentes tramos de cinta o lazo son siempre paralelos. Aunque no siempre aparecen todas, sí que es cierto que todas corresponden a los radios de una circunferencia dividida en un número entero de partes; y en la inmensa mayoría ese entero es par y se expresa usualmente como ‘lazo de 8, de 12, etc. Aparecen así los enteros 4, 6, 8, 10.... Pero no todos son interesantes, por un lado, como el 4 y el 6; ni cómodos y fecundos para realizar diseños, como los números altos. De modo que esa inmensa mayoría de redes emplean 8, 10 y 12. Y sus múltiplos, 16, 24, 20, pero menos frecuentemente.
Llamamos orden de la red N al número de radios de esa circunferencia ideal. En términos de dirección ese número es solo igual al orden cuando éste es impar, caso poco frecuente, con excepción de 9, que suele aparecer en combinación[2] con otras, como 12. Para los órdenes pares, las direcciones diferentes en el plano son la mitad de ese par. De modo que en el orden 8, por ejemplo, hay sólo 4 direcciones diferentes. Entre estos órdenes pares se encuentran los múltiplos de 4, como 8, 12, 16. Pero no 10 ni 20. En las primeras todo radio de la red tiene otro perpendicular también en la red. En cada cuadrante hay naturalmente N/4 radios.
El orden de la red impone un estilo general a los diseños sobre ellas construidos: es un aire de familia que determina en parte el aspecto final o más bien el carácter expresivo de todo el diseño.
Ángulos e intersecciones
Cuando en un plano hay rectas paralelas a n direcciones todas sus intersecciones han de presentar ángulos múltiplos del ángulo mínimo de la red, que el cociente de una circunferencia completa, 360º o 2p radianes, dividido por el número de radios.
a = 2p / N Si N es par, n=N/2, y a= p/n
Este ángulo es un parámetro fundamental de la red.
Cualquier polígono cerrado en esta red tendrá un múltiplo de a en cada vértice.
Cada intersección genera cuatro ángulos a1, a2, a3, a4, iguales dos a dos los opuestos: y suplementarios dos a dos los contiguos:
a1= a3, a2= a4 (a1+ a2 = a3+ a4 = p
Otro parámetro básico es el ángulo inicial del menor de los ángulos (medidos con respecto a la horizontal del punto de vista del observador). Si no hay horizontal (una bóveda, por ejemplo, hace falta otra referencia, como por ejemplo las direcciones de los límites del recinto o panel donde aparecen. En realidad este ángulo inicial está ligado a las simetrías de la red, generalmente heredada por el diseño, y suele ser 0º, lo que favorece la variedad de redes y diseños.
Podemos expresar todo ángulo de una recta con una referencia fija como la horizontal, en función del ángulo a y de un índice o coeficiente i. Si el ángulo inicial a0 vale 0º:
a i = i ai
O bien, si no lo es, haciendo e = a0/a
a i = ( i + e ) a i, entero y 0 =< e <1, fracc.
El resto e es un fraccionario cualquiera en principio común a todas las rectas de la red.
entero y e cualquiera (fraccionario) en principio, pero común para todos los ángulos de la red. O sea, ea es el resto de dividir a0 y a , o bien la operación ‘modulo de’.
Llamaremos haz N al conjunto del un centro con sus N radios o n diámetros, y sus N a intermedios.
Simetría y giros
El sentido estético e incluso simbólico de los diseños de lazo reside sobre todo en sus simetrías. En efecto, cobran entonces una atracción para la mirada que se complace de alguna manera en percibirlas. El centro máximo de esta atracción (o los centros, pueden ser varios) es la zona de mayor simetría que permite el orden de la red, punto que recibe varios nombres: sino o signo, estrella, en español; sol (shams) en árabe y persa. Esta redundancia en los valores es percibida como similitud y parentesco entre partes, uno de los recursos de todo producto estético; como ejemplo paradigmático, en la música.
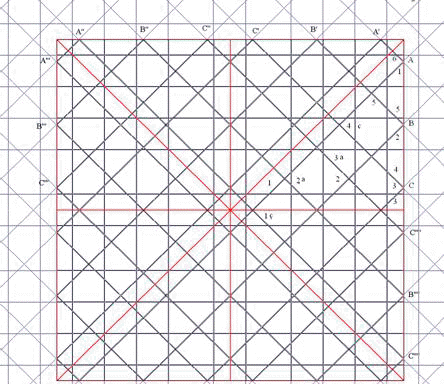
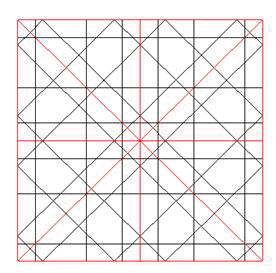
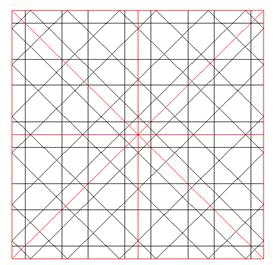
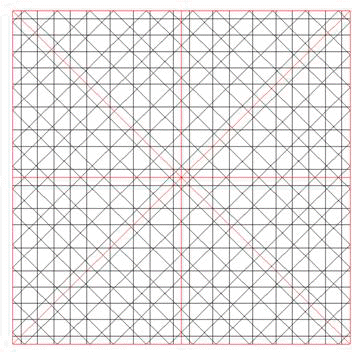
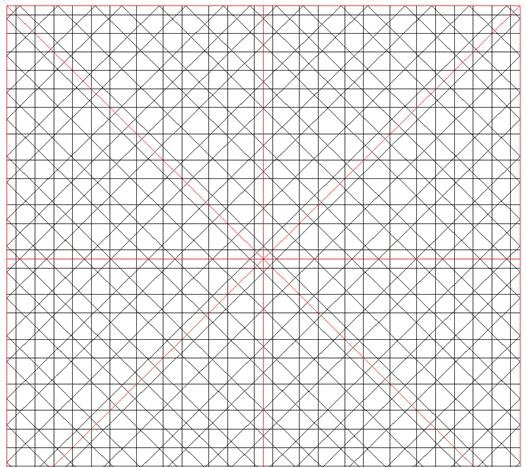
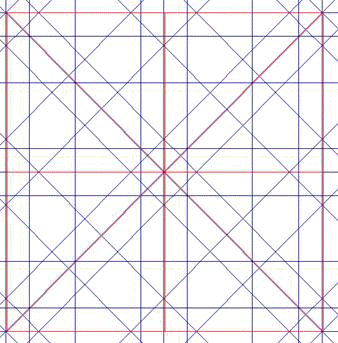
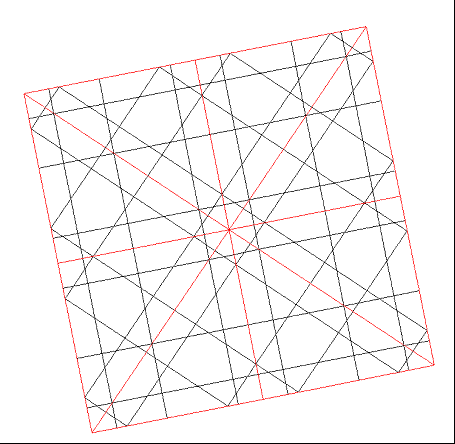
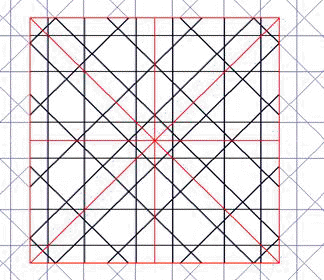
En la red de 8 pueden encontrarse puntos o centros por los que pasan ejes de simetría paralelos a las direcciones principales (4 en realidad) y otras 8 (4 en realidad) de ejes bisectrices de las anteriores. En la de 16, 16 (8) más 16 (8), En la de 10, 10 más 10, 20. Esta multiplicidad genera un juego de espejos en el que la mirada se posa y se detiene en un proceso de apropiación paulatina de la forma. En la figura 1, de 8, encontramos 4 ejes de inclinaciones 0º, 45º, 90º y 135; y también los de 22.5º, 66.5º, 112.5º y 157.5º. Este segundo grupo es menos evidente que el primero, debido a la influencia del recuadro o marco, orientado con el ángulo inicial de la red, 0º en este caso. Pero además la simetría no es total, sólo abarca a la parte central En radianes, los 8 ejes se inclinan 0, p/8, 2p/8, 3p/8, 4p/8, 5p/8, 6p/8, 7p/8.
|
|
|
|
Fig.1 Una red de 8 con sus 8 ejes de simetría |
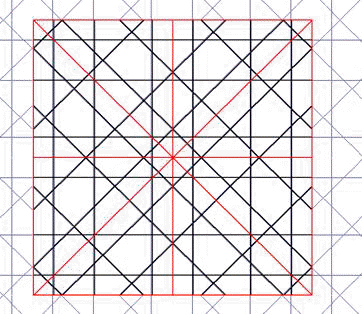
Fig.2. Reflejo aparente en ejes de simetría |
Reflejo y simetría axial
Dos rectas simétricas axialmente parecen cruzarse en un punto del eje, y cada una parece reflejarse dentro de su propio espacio, como lo haría un rayo de luz, debido a la igualdad de los cuatro ángulos de los cuatro segmentos con el eje de simetría. Esta propiedad nos permite saber si dos parcelas de red pertenecen a la misma: todas las rectas deben coincidir a ambos lados del límite, en cada una de ellas. Como se ve en la figura 1. todos los rayos (líneas finas) que cruzan un eje de simetría (línea gruesa) se cruzan en el eje con sus simétricos, produciéndose ese reflejo aparente dentro de cada zona limitado por ejes de simetría (ocho triángulos rectángulos). Toda recta por lo tanto engendra por reflejo nuevas rectas que han de pertenecer a la misma red.
Los ángulos de estas nuevas rectas dependen de los de las primeras y del ángulo del eje de simetría. Así, cuando una recta incidente de ángulo ai (con la horizontal, para fijar una referencia cualquiera) se refleja en un eje de ángulo g , el ángulo del rayo reflejado vale:
a r = 2g - a i (1)
debido a la igualdad de los ángulos de ambos rayos con el eje, de valores respectivos i = a i- g , r = g - a r, como se aprecia en la fig. 2.
Hay algunos ejes particularmente importantes por su frecuencia: los de
ángulos g de valores 0º, 90º
y 45º. Para el primero se obtiene un ángulo reflejado opuesto al incidente:
a r
+
a i = 0º. Es el
refl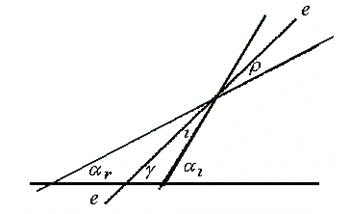 ejo en el agua. Para el segundo se obtiene en ángulo suplementario:
a r
+
a i = 180º . Es como
el reflejo en un espejo vertical. Para el tercero se obtiene en ángulo
complementario: a r
+
a i = 90º. Espejo
pues inclinado. Los tres casos pueden observarse en la figura 1, con un caso
muy común de red de 8.
ejo en el agua. Para el segundo se obtiene en ángulo suplementario:
a r
+
a i = 180º . Es como
el reflejo en un espejo vertical. Para el tercero se obtiene en ángulo
complementario: a r
+
a i = 90º. Espejo
pues inclinado. Los tres casos pueden observarse en la figura 1, con un caso
muy común de red de 8.
Asimismo son interesantes los casos de rayo perpendicular al eje, reflejado en sí mismo, y el de rayo paralelo al eje, el cual tiene simétrico (también paralelo) al otro lado del eje, pero no se ‘refleja’ propiamente, al no cortarle.
Las simetrías imponen varias condiciones importantes sobre los ángulos y, como veremos más adelante, también sobre las distancias entre rectas.
La primera nos llega de esos ángulos de los rayos incidente y reflejado (papeles inmediatamente intercambiables) con el eje, con subíndices i y r. Puesto que ambos rayos son de la red, su ángulo debe ser un múltiplo del ángulo básico, a. Por lo tanto su diferencia (en valor absoluto) es:
a r -a r = (2g - a i) - a r = 2g - 2a i = k a con k = 0, 1, 2 ...
de lo que deducimos que
g - a i = k/2 . a (2)
Así que el ángulo entre el eje y cualquiera de los rayos básicos de la
red

debe ser necesariamente un múltiplo de medio ángulo básico
Es decir, cualquier eje de simetría o es paralelo a la red (es decir a alguna de sus direcciones principales) o lo es a alguna de sus bisectrices. Los ejes de simetría no son pues completamente libres, están ligados a la red. Cuando k es par diremos que el eje es ‘paralelo a la red’. Cuando es impar diremos que el eje está a-semigirado, o, si no hay duda de en qué red nos encontramos (¡podría haber varias en el mismo plano!), simplemente semigirado. En la práctica encontramos ambas formas de simetrías.
Así que en general
g = (e + g ). a con g entero, e de valor nulo o 1/2
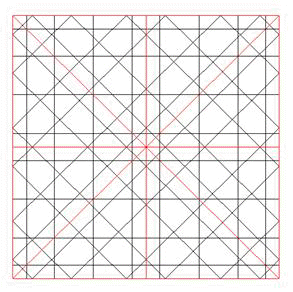
Habitualmente la red está orientada respecto a la horizontal, con ángulo inicial 0º, o está semigirada respecto a ella, con ángulo inicial a0 = a / (2N), mientras que son los ejes los que se mantienen paralelos a esa horizontal, tomada como referencia por nosotros, con sentido de giro positivo el contrario a las agujas del reloj, según es habitual en trigonometría y geometría. En las figuras 3 y 4 podemos ver una red de 12 en dos posiciones no girada y semigirada, con ejes no girados..
Las fórmulas anteriores aplicadas a una red de orden N nos permiten conocer la relación entre los índices de las direcciones principales al reflejarse, relación que depende, como todo, del orden N de la red. La fórmula (1) se expresa en índices como:
(i + r) a = a r =2g - a i =2(s + g ) a) - ( i + ei) a
i + r = 2 (s + g ) - ( i + e)
r = 2 s – i + 2( g - e)
donde el paréntesis es nulo si los ángulos iniciales de red y simetría son iguales, incluido el caso de ser ambos nulos; si no son ambos iguales deben diferenciarse necesariamente en ½ como vimos antes; de modo que si es la red la semigirada en paréntesis vale -1; y si es la simetría, vale 1; en el caso anterior vale 0. O sea, r,s,i son enteros positivos, comprendidos entre 0 y N/2; g, e fraccionaros, nulos o iguales a un medio
Por lo tanto:
r = [ 2 s – i + 2( g - e)] mod N/2 (3)
0 <= r, i, s < N/2, enteros 0 <= g, e < 1, fracc
que podemos expresar también mediante índices únicos fraccionarios suma del entero y su fraccionario menor que 1:
r’ = ( 2 s’ –i’ ) mod N/2 (3’)
0 <= r’, i’, s’ < N/2, fracc. del tipo x = k / 2, k entero
Obtengamos el cuadro de reflejo para unos pocos órdenes con simetrías paralelas (eje paralelo a alguna dirección principal de la red) y semigiradas (paralelos a alguna bisectriz). Considerando primero la red paralela y luego la semigirada (referidas siempre a la horizontal, ángulo 0º trigonométrico).
Estos cuadros permiten obtener el índice r de un rayo reflejado en un eje de índice s. procedente de un rayo incidente de índice i, según la fórmula 2. Comenzamos con el caso de una de red de 10, con direcciones paralelas de red y simetrías.
|
R10|| s|| |
N/2 = 5. e = g = 0 Valores de r |
||||
|
i \ s |
0 |
1 |
2 |
3 |
4 |
|
0 |
0 |
2 |
4 |
1 |
3 |
|
1 |
4 |
1 |
3 |
0 |
2 |
|
2 |
3 |
0 |
2 |
4 |
1 |
|
3 |
2 |
4 |
1 |
3 |
0 |
|
4 |
1 |
3 |
0 |
2 |
4 |
El cuadro nos indica que:
1. Todas las columnas contienen todas las direcciones (los cinco índices de R10).
2. Todas las correspondencias se dan en pares, porque la distinción entre incidente y reflejado es arbitraria, ambos pueden intercambiar sus papeles. Queda pues una dirección invariable en el reflejo: la paralela a la simetría correspondiente. Por ejemplo para s=2 (72º) se asocian los pares: 0-4 y 1-3; 2, paralelo a la simetría, se refleja en sí mismo.
3. En este caso de R10 las diferentes simetrías asocian diferentemente los índices r-i; esto quiere decir que un rayo i determinado se refleja en un r con una simetría y con otro r’ con otra. No hay aquí separación independiente entre pares e impares –como ocurre en R8), lo que nos lleva en último extremo a usar una misma serie de distancias entre rectas para todos los índices, como se verá en el párrafo siguiente. Por ejemplo el rayo 1 inicial reflejándose sucesivamente dentro de un triángulo de ejes de simetría de índices 0, 1 y 3, isósceles de ángulos 36º, 72º, 72º, recorrerá las direcciones: 1(3), 0(1), 2(0), 3(1), 4(0), 1(3)…, volviendo a la dirección inicial (pero no la misma recta en general) tras 5 reflejos y habiendo pasado por todas ellas (no asignamos sentido a estos ‘rayos’, sólo dirección).
Sigamos con de red de 10, con direcciones paralelas de red y simetrías semigiradas. Es como el anterior pero sumando 1 (doble de g) a los valores de r del cuadro anterior y sacando otra vez el módulo 5:
|
R10 || s \/ |
N/2 = 5. e = 0 g =1/2 Valores de r |
||||
|
i / s+g |
0.5 |
1.5 |
2.5 |
3.5 |
4.5 |
|
0 |
1 |
4 |
5 |
2 |
4 |
|
1 |
0 |
2 |
4 |
1 |
3 |
|
2 |
4 |
1 |
3 |
0 |
2 |
|
3 |
3 |
0 |
2 |
4 |
1 |
|
4 |
2 |
4 |
1 |
3 |
0 |
El cuadro nos presenta asociaciones diferentes de las del anterior, pero conserva el mismo comportamiento: dos pares de asociaciones i-r y otro índice que se conserva al reflejar. Una secuencia de reflejos con igual índice inicial y triángulo isósceles girado medio punto (18º) será ahora diferente:
*** 1(3.5), 1(0.5), 0(0.5), 3(1.5), 4(0.5), 1(3.5)…,
|
|
|
|
Las simetrías pueden ser mixtas: por ejemplo un triángulo rectángulo de cateto horizontal y ángulo izquierdo de 36º corresponde en R10 a las simetrías 0, 1, 2.5 (0º, 36º, 90º). La secuencia de reflejos anterior deviene entonces:
*** 1(3), 0(1), 2(0), 3(1), 4(0), 1(3)…,
Distancias, separaciones y orden
Las distancias entre rectas paralelas en la red pueden ser cualesquiera en número y valores. Hay una absoluta libertad inicial para diseñar la red. Pero los resultados de un uso intensivo de esta libertad ‒como por ejemplo eligiendo al azar esas distancias‒ son confusos y decepcionantes: no interesan. Es necesario que la red admita movimientos geométricos que simplifiquen e impongan orden en esa variedad. Especialmente ha de haber simetrías (axiales y centrales) que den lugar a patrones que capten el interés del observador; han de ser pregnantes en la nomenclatura de la Gestalt.
Esta necesidad psicológica y artística reduce enormemente aquella variedad inicial, llegándose en la práctica a la existencia mínima de sólo dos distancias diferentes entre rectas contiguas, dos separaciones que llamamos a, la mayor; y c, la menor. El orden de la red determina la proporción entre esos dos valores pero hay una relativa libertad (también ligada a ese orden) en la elección del número y ordenación de ellas. No es posible sin embargo obtener esos dos valores exactos en general, sólo lo es para algunos órdenes, los habituales R8 y R12. R10 ya presenta problemas y otros, como R14, no son ya teóricamente posibles, aunque sí pueden ser usados en la práctica con algunos retoques.
Con menor frecuencia aparecen también otras combinaciones de ambas separaciones, como c/2, a/2, a-c, pero en áreas del dibujo diferentes, que aparecen así como un elemento local de variación ocasional pero relacionado íntimamente con las dos distancias citadas, las cuales, como veremos, dependen estrechamente de ese ángulo básico 2p/N, que hemos llamado a.
Vamos a intentar demostrar cómo las simetrías citadas imponen esa reducción en el número y valores de esas separaciones. Eligiendo primero un punto arbitrario que consideramos como centro, vamos a codificar todas las rectas de la red en función de su distancia a ese centro y de su ángulo con la horizontal. Obtenemos así unas coordenadas para cada recta r del tipo
r (d, a)
Consideraremos la distancia dotada de un signo: positivo cuando orientándose según el ángulo encontramos la recta a la derecha del centro; negativo si está a la izquierda. Numeramos todas distancias a partir del centro con los índices 1, 2, 3...las positivas y con enteros negativos las negativas. Reservamos el índice 0 para la distancia 0, aunque no haya rectas en la práctica a esa distancia, solo ejes de simetría.
.Esta codificación no es indispensable para establecer periodicidades en las secuencias de separaciones entre rectas contiguas, pero sí conveniente para los cálculos que siguen[3]. El paso de uno a otro concepto es inmediato: cualquiera que sea el centro elegido, se cumple siempre que la separación o distancia entre dos rectas (paralelas) es igual a la diferencia entre sus distancias al centro. Se pasa de distancias a separaciones y viceversa mediante:
di = Σk=1 k=i sk si = di - di-1
Cuando haya que precisar llamaremos interseparación a la separación entre rectas contiguas; pero en general la llamaremos simplemente separación..
En principio hacemos coincidir ese centro con la intersección de los ejes de simetría ligados a la red N que veíamos antes. Asimismo coincide con el centro de simetría central, la que ocasiona giros de sectores circulares.
De modo que para cada ángulo principal de la red encontramos dos secuencias de distancias al centro, una de distancias positivas, otra de negativas, con frecuencia iguales en valores absolutos, (1 y -1, 2 y -2,...), o sea, completan una secuencia capicúa de separaciones.
Para completar la notación, cada distancia de índice i para un ángulo de índice j será llamada d i j. Así la tercera distancia a la izquierda del centro según el ángulo de 90º en la red de 8 paralela (R8||) será llamada d-3 2. Si no hay duda en la serie j a la que nos referimos diremos simplemente d-3
Ahora bien, hay que determinar varios parámetros adicionales para diseñar una red concreta que cumpla con otras condiciones opcionales, también adicionales.
Generación de una red mediante partes de ella
Hay subrredes o partes de la red que pueden encontrarse en la inmensa mayoría de las redes de lacería: su reptición mediante simetrías, giros y traslaciones generan toda la red. .
La elección de ambos polígonos generadores no es única; ya que siempre podemos tomar combinaciones de ellos como generadores de la red, pero suelen elegirse los de menor tamaño, por economía, claridad y parsimonia. Además esos elementos mínimos, BDT y EGR representan una medida de la complejidad inherente de la red: esa complejidad está relacionada con la longitud del código mínimo necesario para describir sin ambigüedad la red, para generarla. A su vez, esa complejidad está relacionada con el tiempo necesario para asumir una forma, para aprehenderla y aprenderla. Para recordarla y para dibujarla de memoria.
Elemento Generador de Red
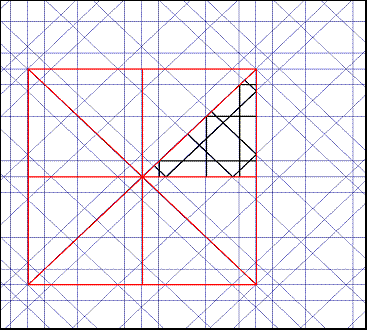 La
primera subrred, EGR es una pequeño polígono, el menor posible, casi siempre
un triángulo rectángulo formado por ejes de simetría.cuya repetición por
simetría axial alrededor del centro cubre un ángulo de 360º.. Cada RGR y su
simétrico generan una figura mayor, como un pétalo cuyo giro sobre el miemo
centro produce el mismo resultado. El EGR puede considerase como medio
pétalo de una flor, generada por giro de esos pétalos. Naturalmente siempre
contamos con un número entero de pétalos y por lo tanto M es siempre par. El
número de pétalos es m = M/2. y el ángulo que subtiende medio pétalo es
llamado b en este estudio.
De modo que
La
primera subrred, EGR es una pequeño polígono, el menor posible, casi siempre
un triángulo rectángulo formado por ejes de simetría.cuya repetición por
simetría axial alrededor del centro cubre un ángulo de 360º.. Cada RGR y su
simétrico generan una figura mayor, como un pétalo cuyo giro sobre el miemo
centro produce el mismo resultado. El EGR puede considerase como medio
pétalo de una flor, generada por giro de esos pétalos. Naturalmente siempre
contamos con un número entero de pétalos y por lo tanto M es siempre par. El
número de pétalos es m = M/2. y el ángulo que subtiende medio pétalo es
llamado b en este estudio.
De modo que
b = 2p / M M par
Este valor b suele coincidir con a o con un múltiplo: cómo: a = 2p/N, entonces
b = 2p / M = M b = a N /M= a N /M
Pero el ángulo de cualquier eje de simetría con la red es necesariamente según (2): g - a i = k/2.
Con lo que b , ángulo de dos ejes, seráigualemnte b = (K / 2) a, es decir M= 2 N / K
Veamos N los valores pares de e M. Para los primeros valores útiles de N (escribimos impares con letra pequeña y no enteros con guión):
| Valores posibles de M | ||||||
| N K | 1 | 2 | 3 | 4 | 5 | 6 |
| 6 | 12 | 6 | 4 | 3 | - | 2 |
| 7 | 14 | 7 | - | - | - | - |
| 8 | 16 | 8 | - | 4 | - | - |
| 9 | 18 | 9 | 6 | - | - | 3 |
| 10 | 20 | 10 | - | 5 | 4 | - |
| 11 | 22 | 11 | - | - | - | - |
| 12 | 24 | 12 | 8 | 6 | - | 4 |
Lo que nos muestra cómo las simetrías axiales y circulares impuestas a la red reduce a muy pocos los posibles valres de N: sólo 6, 8, 9, 10 y 12 admiten la estructura de m = M/2 pétalos descrita. Nuevas condiciones limitarán aún más ese número.
Todo segmento de recta interior al EGR debe continuarse fuera de él sobre su recta y a su vez, debe reflejarse en sus límites indefinidamente. Como cada reflejo debe continuarse fuera del EGR, ya se intuye que hay muy poca libertad a la hora de elegir las separaciones entre rectas de cada haz paraelo. Esta condición va a servirnos para determinar esas secuencias de separaciones sobre cada una de las N direcciones principales.
Bloque de Desplazamiento de Red
La segunda subred, el BDR, es una polígono
que genera toda la red mediante traslaciones en todas las direcciones, a la
manera de baldosas que cubren el plano. Se conocen desde Euler las maneras
de recubrir el plano mediante polígonos regulares iguales (con irregulares
hay infinitas) pero en nuestra disciplina suelen utilizarse las más
sencillas que utilizan una sola figura, principalmente el cuadrado y el
hexágono.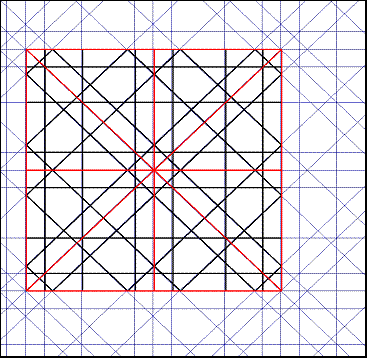 Ese BDR está limitado por ejes de simetría lo que permite las periodicidades
de secuencias de rectas a las que hemos aludido antes, cada período en un
bloque. Generalmente el BDR es precisamente la estructura de pétalos
generada por el EGR. De modo que las formas de ambos están estrechamente
ligadas. Debemos pues comprobar cuales valorews de M son admisible para que
den lugar a un BDR que genere a su vez la red. Puesto los únicos polígonos
regulares que cubren el plano son el cuadrado y el hexágono (el rombo
regular es un cuadrado girado) splp los valores M=8 y M=12 son admisibles
para BDR. Claro está que podemos renunciar a esta subred y general una sola
‘flor’ crciendo radialmente tanto como queramos: pero eso nos obliga un EGR
complicado.
Ese BDR está limitado por ejes de simetría lo que permite las periodicidades
de secuencias de rectas a las que hemos aludido antes, cada período en un
bloque. Generalmente el BDR es precisamente la estructura de pétalos
generada por el EGR. De modo que las formas de ambos están estrechamente
ligadas. Debemos pues comprobar cuales valorews de M son admisible para que
den lugar a un BDR que genere a su vez la red. Puesto los únicos polígonos
regulares que cubren el plano son el cuadrado y el hexágono (el rombo
regular es un cuadrado girado) splp los valores M=8 y M=12 son admisibles
para BDR. Claro está que podemos renunciar a esta subred y general una sola
‘flor’ crciendo radialmente tanto como queramos: pero eso nos obliga un EGR
complicado.
En la figura puede contemplarse el BDR procedente del EGR anterior, cuya simplicidad no no hace evidente la figura generada al rotar.
Periodicidad
|
|
|
|
La primera condición es la periodicidad de la red, es decir, que las distancias entre rectas forman un patrón que se repite periódicamente. Esto no es indispensable, pero la estética largamente ensayada de estas figuras lo hace muy a menudo, llegando así a figuras que se repiten asimismo en varias direcciones. Esto tiene que ver con el retorno rítmico de sucesos, aquí, visuales. Esas periodicidades y coincidencias a intervalos regulares en las dos dimensiones del dibujo dan lugar a poligonales y Riges, también periódicamente repetidas, y a poligonitos simétricos, generalmente.
La mayoría de los diseños de lacería utilizan una red periódica. Estas redes admiten un período en la secuencia de separaciones en todas las direcciones de su orden. O sea, para toda dirección k, de 0 a N-1, se cumple:
Existe al menos un entero pk >0 para el que, para todo índice i de separacion:
s k i = s k ( i + pk ) con 0 < i < pk – 1 para todo k
Encontramos pues una secuencia de longitud pk que se repite indefinidamente en cada una de las k direcciones principales del orden de la red (eliminamos el superíndice k por claridad):
Sk = { s0 s1 s2 ... sp-1 sp }.
Aunque podemos tomar cualquier separación si en S como primera, se trata, como en todos los períodos de una sucesión circular sin un comienzo determinado, de elegir uno arbitrario cualquiera.
Se trata ahora de determinar el número máximo de secuencias k diferentes que estas redes PS (periódica y simétrica) admiten, lo que viene deducido de la fórmula (2) y los cuadros derivados de ella..
.....,
Aunque son conceptos geométrica y aritméticamente independientes, la mayoría de las redes usadas en lacería poseen las tres características simultáneamente; y así las heredan los diseños sobre las que se bordan, por decirlo así.
De esta manera, toda periodicidad en un eje se repite idénticamente en los demás, con lo que todos los períodos en cada dirección son iguales:
p k = p k+j = p
para cualquier dirección j principal (de 0 a n-1)
Situemos dos centros de simetría central de orden N, y ángulo básico a=360/N, a distancia 2x. O sea dos haces N. Comparten el eje 0º (horizontal). Son pues simétricos con eje e en la mediatriz del segmento OO’. Si deseamos que pertenezcan a la misma red los rayos de cada uno que pasan por su centro (d=0) entonces pasarán a una cierta distancia del otro centro.. En particular la distancia así generada O’A = 2x.sen(a). valor igual por simetría a OA’. Si la distancia de la recta OA crece (positivamente hacia abajo, la distancia OA’=O’A decrece en igual valor. La suma de ambas distancias es pues constante. A su vez, el segmento OA = 2x.cos(a). Y por ser normal
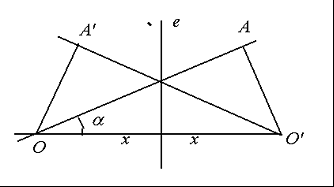
Por ejemplo, el caso más sencillo (dentro de los interesantes), el de 8, con a=45º, genera un rayo en O que pasa a distancia de O’ igual a 2x sen(45º) = 2x. √2 / 2 = √2x . La distancia OA’ aparece..
El caso de 12 es más complejo: el rayo a=30º se refleja en 150º, a distancia alfa
Es decir, cualquiera que sea el valor de x, la disposición de dos haces con centros sobre la misma horizontal crea restas de la red a distancias dependientes de N. Como 2x es también una distancia de dos rayos verticales, comprobamos cómo la disposición anterior crea varias distancias con proporciones dependientes de N.
Valores de las separaciones en la red periódica y simétrica
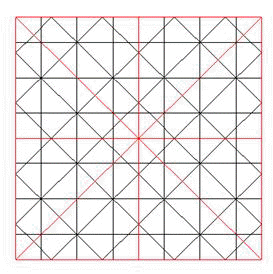
Las condiciones P y S limitan los valores que pueden tomar las distancias entre rectas contiguas. Incluso admitiendo sólo dos redes que las cumplen y otras no. Se comprueba ese efecto comprobando si todas las rectas dentro del Bloque de Red se prolongan en los vecinos o por el contrario, quedan interrumpidas dentro de él.
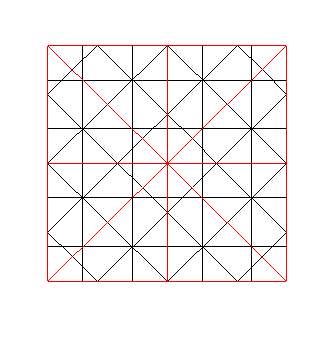
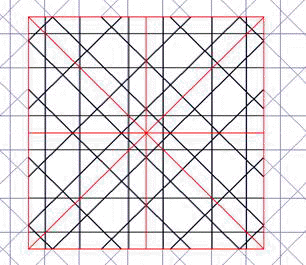
Por ejemplo, la red de la izquierda es simétrica y periódica, mientras que la de la red derecha no lo es
|
|
|
|
|
|
En nuestros artículos anteriores, como(),(),() habamos postulado el número de valores de las separaciones entre rectas contiguas en relación cal orden de la red. El número de valores era de dos esencialmente (junto a combinaciones de ellos). Se ofrecía una relación entre esas distancias cuando eran sólo dos, caso típico y además estético. Esa relación era y es, grados y en radianes:
a/c =2.cos (360º/N), a/c =2.cos (2p / N) (= 2.cos(p /n) )
siendo a y c esas dos distancias, N el número de radios paralelos a esas direcciones y n su mitad, cuando como es habitual N es par. Para una división de la circunferencia en 8 partes, red o lazo de 8, N=8, n=4, a/c=√2 = 1.4142. Así que en toda red de 8 usaremos distancias iguales a una de esas dos, Si c = 1, a = 1.4142.
Vamos a justificar aquí esas relaciones acudiendo a las condiciones de simetría que veíamos más arriba. Expongamos las condiciones que debe cumplir una red simétrica con sólo dos valores de separación.. Nótese que se postulan para los ejes de simetría, no para la red misma, aunque su relación sea estrecha:
El coseno del ángulo b = 2p / M que determina las simetrías radales y giros de la red puede expresarse en la forma m + n √ n, siendo m,n racionales (es decir, quebrados, cociente de dos enteros, de ambos signos); n número natural (entero positivo) primo. Así:
cos (2p / M) = m + n √ n, siendo m,n quebrados; n, entero positivo primo
Si se cumple esta condición nosotros podemos elegir a nuestra vez dos valores de separaciones, como 1 y √ n, De esta manera, en el triangulo EGR emplearemos una combinación lineal cualquiera de esas separaciones que nos sirven como unidades de medida y conseguir una medida, o mejor dos, entera. Sea esos coeficientes de las unidades elegidas l, h .En ese caso se cumple que la proyección de la hipotenusa sobre el cateto vale a su vez: ’
c = a. cos b, = ( m + n √ n) ( l + h√ n,)= ( ml + nh n)+ ( nl + mh) √ n,= l’ + h’ √ n)
donde vemos que también el cateto c admite las mismas unidades de medida que la hipotenusa a.
Puesto que los segmentos tienen sus simétricos contamos en esta red con dos medidas que se nos repiten circularmente y se extienden por el plano mediante la traslación sucesiva del BDR, nuestra baldosa cubriente.
Ahora bien ¿cuáles son las redes que cumplen esa condición?. Muy pocas, precisamente las usadas universalmente para realizar lacería extensas o no. Las redes de 6, 8, 10 y 12. No demostraremos que son las únicas, porque pudiera en principio haber un M muy alto que cumpla esa condición. Pero no sería ya una red visual, perceptiva, constructiva y estéticamente útil.
Listando los valores de los cosenos y el entero n bajo raíz para los primeros valores de M se observa cómo sólo los órdenes 8, 10 y 12 cumplen la condición (no se conoce para otros valores de N) de que el coseno (tomamos el doble para que a sea mayor que c, una convención de nuestra notación dirigida a que c sea la ‘calle’ de las lacerías habituales) se exprese en la forma postulada m + n √ n,. Los demás valores de a/b para otros órdenes se calculan con la misma fórmula por similitud, pero no admiten ya redes simétricas, sólo centros que se expanden más o menos. Los valores de a/c van creciendo regularmente con N, acercándose a 2 sin alcanzarlo nunca.
|
N |
a/b = 2cos(2p /M) |
a/b exacto |
|
6 |
1 |
1 |
|
8 |
1.4142.... |
%2 |
|
10 |
1.6180 ... |
(%5+1)/2 |
|
12 |
1.7320... |
%3 |
|
14 |
1.8019... |
|
|
16 |
1.8477... |
|
|
18 |
1.8793... |
|
|
20 |
1.9021 |
|
Diseño general de redes periódicas/
Ya en Sánchez, 1993 se mostraban las relaciones entre orden de la red (número de direcciones-sentidos de una figura, y las distancias entre rectas paralelas a esas direcciones.
Secuencias
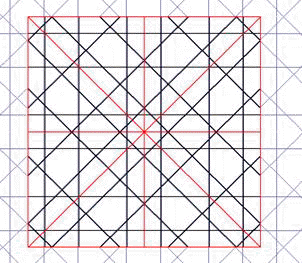
Se consigue esta periodicidad haciendo que los grupos de distancias en direcciones contiguas incluyan combinaciones de a y c tales que coincidan en un triángulo de ángulo central beta b, 45º en el caso de 8. Por ejemplo, en la red de la figura, muy común y fecunda aunque simple, observamos que las verticales y horizontales se repiten con regularidad, en una secuencia infinita de distancias:
...a, c, c, c, a, c, a, c, c, c, a c, ...
es decir con un periodo, cuyo comienzo elegimos arbitrariamente (cualquiera vale en una secuencia periódica): obtenemos [c.a.c.c.c a]. mientras que las oblicuas se disponen en la secuencia:
a, c, a, c, a, c,...
es decir con un periodo [c.a]. (o [a c].) .
Llamaremos a las dos series H y X, correspondiendo la primera a las distancias de la serie horizontal (ángulo alfa
Los comienzos de ambas series son arbitrarios pero están ligados en ambas secuencias: es decir, deben coincidir ambas series en ese comienzo, el más cercano al centro. Así tenemos el par de periodos emparejados: en rojo: [c a.c a] // [c a.c a] .
|
|
|
|
|
|
En general tenemos que recordar las dos fórmulas básicas de la red de 8:
1) que la hipotenusa se proyecta en un cateto. y
2) que dos catetos seguidos se proyectan en (un segmento de longitud igual a) una huipotenusa.
Si el cateto es 1,
2 · cos(45º) = 2 · (√ 2 / 2) = √2
de modo que, si usamos el apóstrofe para significar 'proyectado' (ángulo de 45º) tenemos
a'= c (2c)'= a (1)
o sea, que una combinación de distancias acumulada (en cualquier orden) de [ba+2gc] se proyecta como
[ga+bc]. Esta comprobación determina si en efecto esas combinaciones, en cualquier orden, forman un triángulo generador apropiado.
[ ba+2gc ] ' = [ ga+bc]. (2)
De modo que toda combinación de a y c en diagonal sufrirá esa transformación en la proyección. Así nos obliga a
tener siempre una combinación par de c en las diagonales.
Veamos combinaciones posibles
X [a] H [c] . X [c c] H [ a] . X [a c c] H [ c a] y también. X [c a c] H [ a c]. X [c c a]H [ a c] ,es decir permutaciones al azar de los segmentos requeridos.
X [a a c c] H [ c c a ] y sus permutaciones X [a a c a c]-H [ c c c a ] y sus permutacionesy así sucesivamente.
Recuérdese que los ejes de simetría, en rojo, a partir de los cuales se miden las distancias, no pertenecen a la red, solo la ordenan y marcan simetrías. De igual manera que el espejo no pertenece ni al espacio original ni al reflejado. O el guarda, que organiza la circulación pero no circula.
Sin embargo, no bastan esas condiciones: por ejemplo invirtiendo a y c en la figura, obtenemos: la figura actual (a la izquierda), con la codificación:
RED 8 Recto: H [çacç: 4] Oblicuo: X [çcaaç: 5]
que ya no es periódica en todas direcciones. ¿Qué falta?.
Se observa en este caso cómo las diagonales no llegan juntas a la periferia (en rojo). Para que eso ocurra cada diagonal debe comportarse como un rayo de luz que se refleja (con inclinación de 45º en esta red de 8) en esa periferia, lo que se justifica en Redes periodicas de 8. Allí vemos que ello sólo sucede cuando la codificación de la
semisecuencia oblicua es capicúa
La recta no influye, es paralela a la periferia y por lo tanto siempre coinciden esas rectas al trasladar y copiar de arriba y abajo y hacia los lados el bloque de red. que representamos rodeado de rojo en las figuras.
Si cumplimos las leyes así encontradas
(empíricamente, es verdad) tenemos una guía
 segura
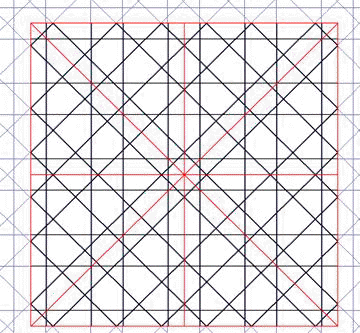
para dibujar redes de 8 periódicas. Un ejemplo:
segura
para dibujar redes de 8 periódicas. Un ejemplo:
RED 8 Recto: H [çacaç: 5] Oblicuo: X [çacccaç: 7]
Secuencias simétricas
Si además queremos figuras simétricas respecto a varios ejes ‒generalmente paralelos a las direcciones principales‒ tenemos que disponer las distancias anteriores de modo también simétrico. Esto nos conduce a desechar algunas de las combinaciones posibles que no lo son. Las que quedan son del tipo
[ cuc ] = inv [ cuc ] (3)
como las frases capicúa del tipo 'lava la bala' o 'daba la zorra arroz al abad'. Así nos quedan las formas
X [ c a c] -H [ c a c]
X [ c c a .c c ] -H [ a c a]
X [ c c a. c c ] -H [ a c c a]
X [ c c a.a c c ] -H [ c a a c]
en las que comprobamos que se cumplen rigurosamente las leyes (1) y (2) ....
Descentrado
Hay más condiciones: si queremos que las rectas de la red se crucen dos a dos, debemos descentrar las rectas, es decir, evitar que coincidan con los ejes de simetría. Para ello desplazamos esas rectas la mitad de una de las distancias.
Si elegimos 'c' como la distancia partida, y llamamos a esta mitad 'ç' entonces obtenemos de las soluciones anteriores las siguientes:
x [ ç a c ç] -H [ ç c a ç]
y vemos que ya no es capicúa.
Las condiciones se han endurecido: ahora debe haber un número par de c en la serie oblicua, porque cada pareja deviene 'a'.
La condición de capicúa obliga a que el número de 'a' (que devienen 'c' cada una al proyectar) sea igual al de a, porque al proyectar devienen un número.
Su además deseamos calles en los extremos del periodo, o sea, medio c, 'ç' en ellos, esto nos obliga además:
Ls ç de los extremos de la sucesión en cruz (-H) nos requiere otro c
Rehacemos los cálculos y obtenemos el siguiente valor mínimo simétrico, descentrado y capicúa:
X [ ç c a c a c ç ] -H [ ç a c a ç ] (4)
que cumple
[ ç c c a c ç ] ' = [ c c c c a a ] ' = [ c c] ' + [ c c] ' + [ a a ] ' =
= [a] + [a] + [c c] = [ç a c a ç ]
Nótese que encontramos un valor obligado c, una calle en el centro de cada una de las series, siempre teniendo en cuanta que henos obligado a media calle en los extremos.
Este valor mínimo puede ampliarse de modo que se sigan conservando todas las condiciones; para ello añadimos siempre un valor par de a en oblicuos (que pasan a rectos como par de c), o cuádruple de c (que pasan como un par de a). Veamos ambos casos:
X [ ç a c a c a c a ç ] -H [ ç c a c a c ç ]
añadiendo 2a cerca de los extremos del oblicuo y 2c cerca de los extremos del recto. O bien:
X [ ç c a a c a a c ç ] -H [ ç c a c a c ç ]
añadiendo 2a cerca del centro del oblicuo y 2c cerca de los extremos del recto. Cabe cualquier combinación en cada una de las series rectas y oblicuas, pero siempre conservando la simetría respecto al centro en cada una. Así que simbolizamos esa libertad poniendo entre paréntesis la zona permutable, reflejada en un paréntesis simétrico en la otra. Así las cuatro posibilidades apuntadas quedan reflejadas en el esquema:
X [ ç ( a c a ) c ( a c a ) ç ] -H [ ç ( c a) c ( a c ) ç ]
Nótense las simetrías de esos paréntesis respecto al c central de cada secuencia. La permutación es libre en cada serie: es decir permutamos la parte libre de las oblicuas con independencia de la permutación en las rectas. La repercusión de una u otra elección consiste en una mayor coincidencia de vértices en la red consiguiente. Ya veremos esto en la práctica.
Para resumir aún más, podemos escribir sólo la mitad del capicúa, recordando que el c central es independiente e inamovible.
X [ / c / ( a c a ) ç ] -H [ / c / ( a c ) ç ]
donde la barra inclinadas rodeando al c central indican que la parte a su derecha ha de copiarse en espejo a la izquierda de la otra.
El caso mínimo es
X [ / c / (a c) ç ] -H [ / c /(a) ç ]
que podemos recodificar más concretamente como
X [ // ç (a c) ç ] -H [// ç (a) ç ] (5)
que interpretamos como: la semisecuencia a la derecha de las dos barras inclinadas (slash) la copiamos en espejo, en reflejo a la izquierda. Esta codificación la llamamos el par de semisucesiones mínimas o generatrices, ya que contienen toda la información necesaria para generar la red en forma mínima o condensada del todo.
Las permutaciones dentro de los paréntesis nos permiten dos posibilidades en las series oblicuas.
X [ // ç a c ç ] -H [ // ç a ç ] y X [ // ç c a ç ] -H [ // ç a ç ]
Ahora podemos comprobar que la red de la figura es una de las disposiciones de la mínima, precisamente la primera:
X [ ç a c a (çç) a c a ç ] - H [ ç c a (çç) a c ç ]
que se reparte a cada lado de la simetría central dividiendo el dos la calle (c) central, en dos mitades o semicalles (ç):
X [ ç a c a (ç ç) a c a ç ] - H [ ç c a (ç ç) a c ç ]
Al prolongar este período indefinidamente se obtiene la serie que encontrábamos empíricamente al principio:
X [...c a c a c a c a c a c a c...] – H [...c c c a c a c c c a c a c c c a c a c c c ...]
pero ahora sabemos mucho más. Podemos general indefinidamente redes más y más complicadas.
Como decía el sabio oriental 'primero estaba la montaña, después no hubo montaña y al final hubo montaña'.
Nos queda ahora otro escollo no obstante lo mucho avanzado:
No todas las redes así generadas forman una red periódica en todos los sentidos. Por ejemplo, veamos la red de la figura, que corresponde a un caso real, es decir, encontrado en algún edificio tradicional.
Veamos otro caso, más complicado, el definido en nuestra notación por:
R8: X [ á c a c a c c a c a c á:12]- H [á c c a c a c c á:9]
Se observa la simetría especular de la semisucesión, es decir, es capicúa a su vez. La sección a cada mitad del eje de simetría del Bloque de Translación, cada cuadrante en este caso es a su vez simétrico en las distancias y por lo tanto simétrico en la figura: cada cuadrante admite ejes de simetría centrales.
|
|
|
|
La novedad reside aquí en que en lugar de colocar semicalles en los límites de las sucesiones y semisucesiones de anchura menor, la llamada 'c' en esta se usan semicalles de la mayor, 'a'.
Nótense que se cumplen las condiciones (1): y (2) :
X ' = H
,o sea
[ á c a c a c c a c a c á]' <> [ 5a 6c] ' = [ 5c 3a] <> [ á c c a c a c c á]
L a red anterior se usa como fondo o textura en unos azulejos de la mezquita del viernes, en Isfahan. Se estudia en Sánchez(1996).
Hay que recordar sin embargo, que esta simetría de la semisecuencias que produce la red infinitamente periódica es sólo una elección: si no se desea esa infinitud, una red de semisecuencia no periódica (si la sucesión) es elegible.
Sumarizamos las leyes empíricas encontradas, suficientes para obtener una infinidad de redes de 8 periódicas en todos los sentidos.
1. Coeficientes de las combinaciones lineales de a y c en oblicuo X y recto H cumplen:
X[ ba+2gc ] ' = H[ ga+bc ]. (1)
2. X es capicúa:
X[ i ] = X[ loX - i ]. (2)
siendo loX la longitud de la semisecuencia oblicua X.
Insertamos estas condiciones en nuestro programa PUERTRA, lo que nos permite obtener y dibujar fácilmente estas redes.
Con los resultados elaboramos un catálogo de redes de 8, virtualmente infinito, ya que ofrecemos los primeros o más sencillos casos y una regla para ampliaros indefinidamente. Se justifica todo esto con más rigor en
Redes periódicas de 8
En nuestro Diseño de redes de 8 hemos visto empíricamente las condiciones que deben cumplir las semisecuencias que definen el bloque de red para que al repetirse por translaciones vertical y horizontal se genere una red única en la que todos los bloques quedan colocados, es decir, sus rectas de red coinciden con las de la red general.
Veamos en detalle la justificación de esas reglas, una en realidad:
la semisecuencia oblicua debe ser capicúa
c
|
|
|
|
omo la de la figura, que es: X [//çaacaaç: 7]: . Siete elementos pues, siete distancias
que podemos ver en la figura.
En ella encontramos los puntos A, B y C en la periferia ‒en rojo.‒ vertical derecha del bloque de red.
Vemos que en esos puntos concurren, son generados por, dos rectas oblicuas con ángulos de 45º y 135º. Su ordenación desde sus ejes de simetría , escritos dentro son
A, 6 - 1 B, 5 - 2 C, 4 - 3
 o
sea suman en todos los casos 7, la longitud de la semisecuencia.
o
sea suman en todos los casos 7, la longitud de la semisecuencia.
Geométricamente eso significa que las suma de los segmentos de cada par de rectas dentro del bloque es constante, o, lo que equivale, también es constante la suma de los segmentos concurrentes dentro del triángulo en rojo limitado por la horizontal central, diagonal de 45º y la vertical a la derecha, lo que llamamos elemento generador de red. Nombre justificado porque por simetrías repetidas respecto a los ejes de simetría, en rojo, qu no pertenecen a la red, se ge
RED 8 Recto: H [çacç: 4] Oblicuo: X [çcaaç: 5]
La situación se repite en el triángulo
simétrico al generador respecto a la bisectriz
 principal,
con los puntos homólogos A', B', C' y en los demás simétricos con los tríos
A",B",C";A"', B"', C"' y así sucesivamente hasta 8 veces..
principal,
con los puntos homólogos A', B', C' y en los demás simétricos con los tríos
A",B",C";A"', B"', C"' y así sucesivamente hasta 8 veces..
La no constancia de esa suma, igual a la longitud de la semibisectriz principal, conduce al caso 3º, en que la red interior no genera la exterior.
Se ven estas redes periódicas en Catálogo de redes 8.y se comprueba en todas el cumplimiento de la condición encontrada.
Caso general
Distancia y ángulos en redes periódicas de 12 (‘)
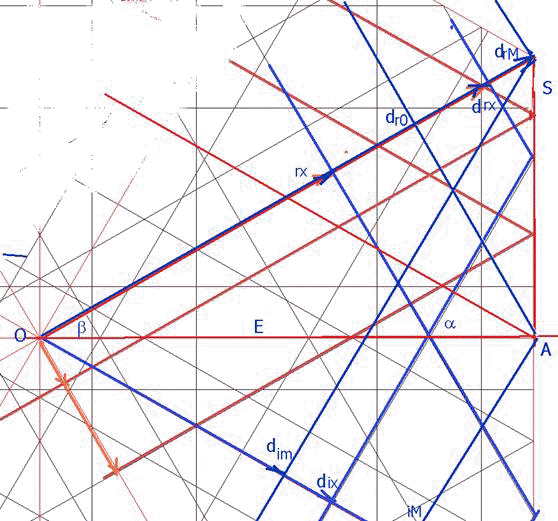
De modo que nos enteramos ahora de que:
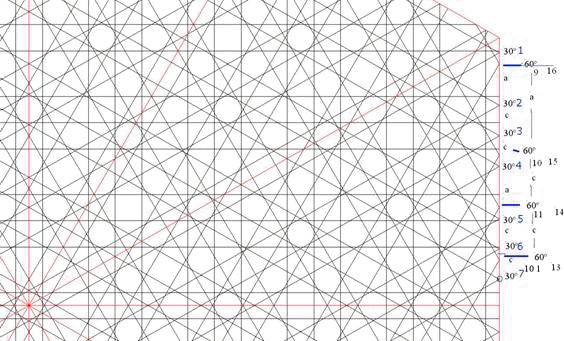
1. La suma de las distancias de los rayos incidente y reflejado en constante. De modo que lo que en una serie determinada (determinada por su ángulo ai) se van separando los incidentes, va aumentando en los reflejados. Así se ve en los rayos rosa de la figura 1, uno a distancia c/2 , la primera, que se refleja en la cuarta, a distancia c/2+c+a+c. Si nos fijamos en el otro, de incidente a distancia c/2+c, la segunda, vemos que se refleja en la tercera distancia, c/2+c+a. De modo que lo que aumenta el incidente, en este caso la distancia a, lo disminuye la reflejada, en igual cantidad. Igual comportamiento presentan la serie de 60º, en azul, que alterna las distancias 2ª y 4ª con las 4ª y 3ª , con diferencia constante también a en este caso.
O sea, para el par de rayos incidente y reflejado se cumple:
1. la suma de distancias es constante: ej: (c/2+c+a+c)+(c/2) = (c/2+c+a)+ (c/2+c) en la serie 30º. Que es igual a la última distancia, en este caso la quinta, (c/2+c+a+c+c/2)
2. la diferencia de distancias es creciente, con constantes. (c/2+c+a+c)-(c/2) = (c/2+c+a)-(c/2+c)
En relación a las semisecuencias X y H el par que nos definen todas las series de distancias, repitiéndose alternadamente en todos los ángulos, tenemos que cualquier elemento s de una semisecuencia define una distancia al origen igual a la suma de todas las anteriores con ella misma.
di = S1-i si
dr = S1-i sr
di + dr = df
Es decir, si el rayo incidente abarca los primeros elementos de la semisecuencia, el reflejado abarca los restantes, que deben coincidir con loa primeros hasta un punto que equidista del centro.
Esto nos conduce al carácter capicúa de la semisecuencia que encontrábamos empíricamente en la página Redes periódicas de 12 y Diseño de redes de 8
dr = S1-i sr
dr = df - S1-i sr
Condiciones de reflejo en SS
|
|
Condiciones de Periodicidad mediante rayos en reflejo |
|
|
|
m0 mu an_in porc.cent.capicua |
|
|
Red 8 |
0 0 0.00
9999.00
0.5 0
22.50 241.42 |
|
|
Red 10 |
0 0 0.00
9999.00
0.5 0
18.00 223.61 |
|
|
Red 12 |
Red 12 __________________________________________________________________ m0 mu an_in %.cnt.cap n.dist SS Lm.Inf,Cent,Lm.Supe SS%- ....no semigiro inicial..... 0 0 0.0 101.00% 5 0 1 3 5 : [|çc/a\cç|]: [//çcacç] 0 2 60.0 33.33% 5 0 2 3 4 : [ç|c/a\c|ç]: [//çcacç] 0 4 120.0 33.33% 5 0 2 3 4 : [ç|c/a\c|ç]: [//çcacç] 0 1 30.0 100.00% 5 1 1 3 5 : [|ça/c\aç|]: [//çacaç] 0 3 90.0 0.00% 5 1 3 3 3 : [ça|/c\|aç]: [//çacaç] 0 5 150.0 100.00% 5 1 1 3 5 : [|ça/c\aç|]: [//çacaç] ....semigirado inicial..... 0.5 0 15.0 215.47% 5 0 1 3 5 : [|çc/a\cç|]: [//çcacç] 0.5 2 75.0 15.47% 5 0 3 3 3 : [çc|/a\|cç]: [//çcacç] 0.5 4 135.0 57.74% 5 0 2 3 4 : [ç|c/a\c|ç]: [//çcacç] 0.5 1 45.0 57.74% 5 1 2 3 4 : [ç|a/c\a|ç]: [//çacaç] 0.5 3 105.0 15.47% 5 1 3 3 3 : [ça|/c\|aç]: [//çacaç] 0.5 5 165.0 215.47% 5 1 1 3 5 : [|ça/c\aç|]: [//çacaç] __________________________________________________________________ |
|
|
Red 16 |
0 0 0.00
9999.00
0.5 0
11.25 208.24 |
|
|
|
|
|
Otro caso complicado
|
|
|
Red 12. X [//çaccaccacaccaccaç: 17] H [//çaccaccaccaccaç: 15]. sX[ 6a+ 10c ] sH[ 5a+ 9c ]. Dispos: dx=1. dy=0.87 dz=0.5 |
Esta red es empírica: Red 12.
H cumple [//çaccacc c ccaccaç: 15] la condición de 100% capicúa desde el centro. En la figura se aprecian, para ai=30º, los reflejos en vertical (desde arriba) las 7 primeras, ç acc acc, que se reflejan simétricamente, de manera capicúa, en las 7 últimas. Es decir, (en negrita y separado)
H [//çaccacc c ccaccaç: 15]
Así que parece que solo queda libre la central, que claro, no quebrantaría la simetría (aunque su valor es fijo, sumando de la proyección adecuada de X (regla1, ver más bajo). De modo que:
SS H debe ser simétrica (capicúa)
Pero X, ángulo 60º: çaccacca c accaccaç
Rn X , aparecen los pares de rayos a 60º ()ver figura) , separados por las distancias_
: 9-16, a 10-15 c 11-14 c 10-13
Es decir, se aparean (???) simétricamente en el sector marcado en negrita.
Red 12. X [//çaccacca c accacca ç: 17]
Esa sub-semisecuencia (SSS) debe ser simétrica. ¡ Pero sólo ella.!
Lo cual quiere decir que las demás distancias son intercambiables permutables (lo que cambia su situación pero no la suma, es decir, las distancias que nos interesas, desde la 9º a la 16º. La 16, no importa porque cae fuera del sector vertical del eEGR.
Probémoslo, intercambiando al azar (no cambiando sin más , por4que ha de conservarse la condición de proyección, la regla 1ª: 1. Coeficientes de las combinaciones lineales de a y c en oblicuo X y recto H cumplen: En esta red 12, como se veía en Diseño empírico de redes de 12, es:
X[ 2ba+2gc ] ' = H[ ga+3bc ]. (1)
Y en efecto, es periódica
Red 12. X [//acca çaccc accacca ç: 17] H [//çaccaccaccaccaç: 15]. sX[ 6a+ 10c ] sH[ 5a+ 9c ] Ss
obtenida permutando las mitades de la parte libre de 1 a 8 en X. Véalo en figura 3.
|
|
|
Red 12. X [//accaçacccaccaccaç: 17] H [//çaccaccaccaccaç: 15]. sX[ 6a+ 10c ] sH[ 5a+ 9c ] |
De modo que permutando arbitrariamente entre sí la parte no negrita y por otra parte, haciéndolo con la negrita y manteniendo su periodicidad, obtendremos redes periódicas de 12.
Estas condiciones son menos duras, más permisivas que las expuestas anteriormente, e Disegno de redes de 12
Distancias entre puntos de reflejo
Se observa que los puntos de reflejo en el la pared vertical se espacian diferentemente. A veces coinciden los de series (ángulos) diferentes) a veces no. Cabe preguntarse sobre la repercusión estética de esta distribución de puntos de reflejo, en el segmento vertical y en los demás. Incluso, al observan los círculos aparentes que aparecen dentro del triángulo EGR, que no son otra cosa que puntos de simetría radial mayor o menor, completa o incompleta, tenemos que preguntarnos sobre la elección de distancias, de las SS X y H, siempre dentro de la periodicidad elegida (recordamos que no es indispensable, cabe perfectamente una red no periódica, que se expande más u más hacia la periferia, sin bloques de desplazamiento.
Todo ello pretendemos estudiarlo en distribución de puntos de reflejo
Catálogo de redes de 8 (perteneciente a Decoración Geométrica Islámica)
A partir del estudio en Diseño de redes catalogamos entre las infinitas posibles las más sencillas en forma escalonada y creciente desde la mínima. Recordamos que la codificación de cada una consiste en:
1. Orden de las red.
2. Semisecuencias de las distancias entre paralelas de las series oblicua (X) y recta (H), a partir del eje de simetría principal del bloque de traslaciones, con su número al final. Entre paréntesis cuadrados. Los paréntesis redondos (estos sí añadidos manualmente) representan posibilidad de permutación libre (cumpliendo eso sí con la condición de capicúa de la semisecuencia oblicua. Aparecen los siguientes símbolos de esas distancias::
a; mayor c; menor á; mitad de la mayor ç; mitad de la menor â, diferencia entre mayor y menor o, nula. 3. Suma de ellas en unidades a y c, las dos distancias principales cuya relación depende del orden. 4. Relación o cociente a/c.Recordamos que nos limitamos a redes con sólo dos distancias entre paralelas (ello excluye en realidad a la distancia â, que sería una tercera. .Nótese también que las medias distancias devienen una entera al repetir el bloque por simetría.
Pero primeramente veamos esta serie de redes generadas cada una de la anterior por adición de nuevas distancias, siempre cumpliendo las condiciones que vimos en ^
1. Proyección de X en H: : X[ ba+2gc ] ' = H[ ga+bc ]. (1) 2. X capicúa: X[ i ] = X[ loX - i ]. (2)Estas dos leyes nos proponen un modo de generación de nuevas redes a partir de las anteriores mediante la adición en de una distancia 'a' o mediante la adición de dos distancias c. Se nos presenta un triángulo parecido al de Tartaglia al disponer las secuencias oblicuas en orden creciente:
a2c 2a2c a4c 3a2c 2a4c a6c 4a2c 3a4c 2a6c a8c 5a2c 4a4c 3a6c 2a8c a10c ... ... ... ... ... ... ... ... ...Encontremos cuáles son los pares de semisecuencia que cumplen con estas sumas.
| sX [a2c] sH [ac] | ||||||
| X [//áccá: 4] H [//ácá: 3] | ||||||
| sX [ 2a2c ] sH [a2c] | a4c | |||||
| X [//çacaç: 5] H [//ç(ac)ç: 4] | ||||||
| 3a2c | 2a4c | a6c | ||||
| 4a2c | 3a4c | 2a6c | a8c |
|
Semicalles c |
SUMA |
Añado X |
Semicalles a |
|
no |
sH[ 1a+ 1c ] sX[ 1a+ 2c ] |
- |
H [//ácá:3] X [//áccá::4] |
|
H [//çacç:4] X [//çacaç:5] |
sH[ 1a+ 2c ] sX[ 2a+ 2c ] |
a |
|
|
H [//çacç:4] X [//çacaç:5] |
sH[ 2a+ 2c ] sX[ 1a+ 4c ] |
2c |
|
|
|
sH[ 1a+ 2c ] sX[ 2a+ 2c ] |
|
|
Veamos ahora el catálogo anunciado, desde la mínima, las mínimas en realidad, porque podemos elegir semicalles de anchura 'c' o semicalles de anchura 'a'.
La codificación la ofrece el programa PUERTRA, no está retocada ni editada, y corresponde a la figura que aparece encima.
Las ordenamos por tamaño total, es decir, por el tamaño de la suma ba+2gc]. Colocamos juntas las opciones obtenidas por permutación de los elementos en los paréntesis. Representamos a igual escala, manteniendo los valores de las distancias a y c en el dibujo para que se aprecie el crecimiento de tamaño junto a la de complicación.
|
|
|
|
No hay equivalente |
RED 8 Recto: H [//ácá: 3] Oblicuo: X [//áccá: 4] sH[ 1a+ 1c ] sX[ 1a+ 2c ] a/c= 1.4142135623731 |
Añadimos 2c a la semisucesión oblicua en ambos casos:
|
|
|
|
|
RED 8 Recto: H [//çacç: 4] Oblicuo: X [//çacaç: 5] sH[ 1a+ 2c ] sX[ 2a+ 2c ] a/c= 1.4142135623731 |
RED 8 Recto: H [//çcaç: 4] Oblicuo: X [//çacaç: 5] sH[ 1a+ 2c ] sX[ 2a+ 2c ] a/c= 1.4142135623731 |
RED 8 Recto: H [//áccá: 4] Oblicuo: X [//ácacá: 5] sH[ 1a+ 2c ] sX[ 2a+ 2c ] a/c= 1.4142135623731 |
Cuatro ejemplos similares permutando las semisecuencia oblicua y recta, cumplendo siempre las condiciones previas.
|
|
|
|
RED 8 Recto:H [//çacaç: 5] Oblicuo:X[//çcacacç:7] sH[ 2a+ 2c ] sX[ 2a+ 4c ] a/c= 1.4142135623731 |
RED 8 Recto: H [//çaacç: 5] Oblicuo: X [//çcacacç: 7] sH[ 2a+ 2c ] sX[ 2a+ 4c ] a/c= 1.4142135623731 |
|
|
|
|
RED 8 Recto: H [//çacaç: 5] Oblicuo: X [//çacccaç: 7] sH[ 2a+ 2c ] sX[ 2a+ 4c ] a/c= 1.4142135623731 |
RED 8 Recto: H [//çaacç: 5] Oblicuo: X [//çacccaç: 7] sH[ 2a+ 2c ] sX[ 2a+ 4c ] a/c= 1.4142135623731 |
|
|
|
|
|
RED 8 Recto: H [//çcaaç: 5] Oblicuo:X [//çcacacç:7] sH[ 2a+ 2c ] sX[ 2a+ 4c ] a/c= 1.4142135623731 |
|
|
|
|
|
|
RED 8 Recto: H [//çacccç:6] Oblicuo: X[//çaacaaç:7] sH[ 1a+ 4c ] sX[ 4a+ 2c ]a/c= 1.4142135623731 |
|
Como aplicación de la potencia del método elijamos una red complicada, cuya proyecto y comprobación manual llevaría horas, días incluso:
cumpiendo las reglas generamos la red de parámetros:. Elegimos una semisecuencia derecha voluntariamente asimétrica para comprobar el cumplimiento de nuestras reglas de generación.
|
|
|
|
RED 8 Recto: H [//çacaaccccç: 10 ]Oblicuo: X [//çaacacccacaaç: 13] sH[3a+ 6c ] sX[ 6a+ 6c ] a/c= 1.4142135623731 |
|
Un caso más, aún más complejo
|
|
|
|
RED 8 Recto: H [//çacaaccccç: 10]Oblicuo: X [//çaacacccacaaç: 13] sH[ 3a+ 6c ] sX[ 6a+ 6c ] a/c= 1.4142135623731 |
|
Nótese como siempre el 'reflejo' aparente de todas las rectas de la red en los límites y ejes de simetría, en rojo, que aseguran la prolongación correcta de la red interior en el exterior, hasta el infinito.
Puede ahora visitar el Catalogo de redes 12, con igual filosofía y presentación.
Condiciones
La condición de periodicidad establece condiciones sobre las distancias entre rectas contiguas en el período-. La condición de estética y parsimonia establece el uso de un número muy pequeño de interdistancias, dos, generalmente. El orden de la red establece la proporción entre ambas interdistancias. La condición de simetría radial o giro establece al el uso de muy pocas series de distancias diferentes radialmente, dos generalmente. Todas estas condiciones configuran las redes interesantes en la lacería entre las infinitas virtualmente posibles.
Conclusiones
Las condiciones de simetría axial y central en las redes o familias de rectas paralelas permiten encontrar unas sencillas condiciones que deben cumplir las distancias entre esas rectas. Podemos así saber sin dibujarla si una red es periódica y simétrica, o inversamente, formar una red nueva con la seguridad de que lo será. A partir del conocimiento de la red es posible abordar con toda generalidad el estudio de las lacerías que sobre esas redes se diseñan, desligando el estudio de los métodos y teorías con que se originaron..
Bibliografía
Sánchez, F.J. (1993.) "PUERTRA: a Model of Islamic Rectilinear Interlaced Lattices". Proc. 4th. ICEMCO. Cambridge: Univ. Cambridge.
Sánchez, F.J. (1995) "A Model of Islamic Rectilinear Interlaced Lattices". Interactive Internet version:
Sánchez, F.J. (1996) "Lacework Analysis: Three Tilework Panels from Isfahan". Proc. 5th ICEMCO, Cambridge. Cambridge: Univ. Cambridge. http://isfahan.apu.ac.uk/puertra4/index.html
Sánchez, F.J. (1997) "Lacería Islámica en Paneles". Exposición ‒texto y gráficos‒dentro de Los Cinco Sentidos en el Islam", en El Centro de Estudios Islámicos de Madrid.
[1] Centro de Tecnologías Físicas. CSIC. Serrano, 144. Madrid. España.
[2] Estas mezclas de redes en el mismo plano, que hemos llamado metabole en nuestros escritos no serán tratadas en este artículo; lo haremos en otros sucesivos)
[3] y así se han codificado en nuestro programa Puertra con su compleja codificación de redes.


 º
º