Reflejo en el Triangulo Generador de Red
(perteneciente a
Decoración Geométrica
Islámica)
En nuestros intentos de generalizar la red
nos hemos encontrado con un triángulo cuyas copi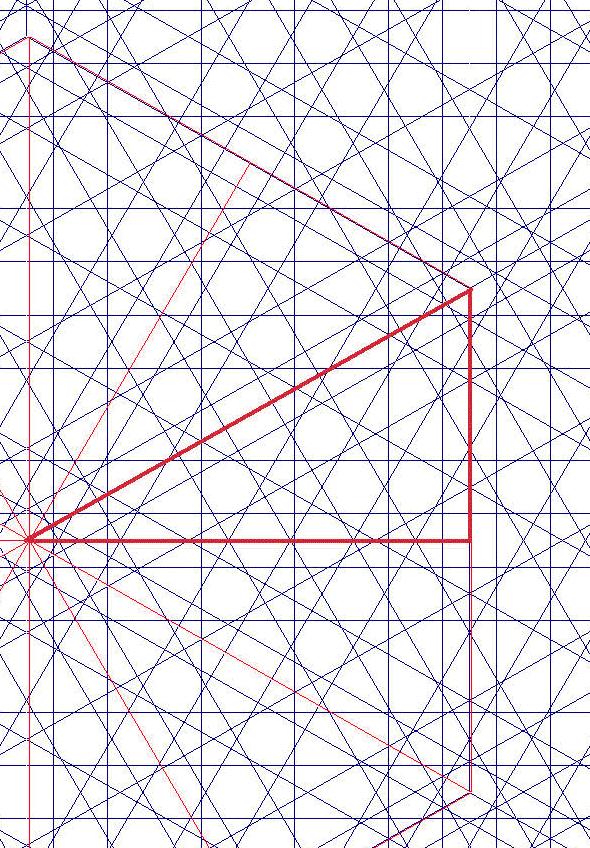
as por simetrías generan
toda la red periódica. Veamos como el reflejo aparente de las rectas de la red
en ese triangulo las genera fuera de él, en todas sus copias. Tomamos la
figura contigua que corresponde a una red de 12, pero el razonamiento se
llevará a cabo de manera general
De modo que toda combinación de a y c en
diagonal sufrirá esa transformación en la proyección. Así nos obliga a
tener
siempre una combinación par de c en las diagonales. Ley 1
Veamos combinaciones posibles
X [a] H [c] .
X [c c] H [ a] .
X [a c c] H [ c a]
y también X [c a c]
H [ a c] X [c c a] H [ a c] ,
X [c a c] H [ a c] .
y sus permutaciones
X [a a c c] H [ c c a ]
y sus permutaciones
X [a a c a c]-H [ c c c a ]
y sus permutaciones
y así sucesivamente.
Recuérdese que los ejes de simetría,
en rojo, a a partir de los cuales se miden las distancias, no pertenecen
a la red, solo la ordenan y marcan simetrías.. De igual manera
que el espejo no pertenece ni al espacio original ni al reflejado. O el
guarda, que organiza la circulación, pero no circula.
Sin embargo, no bastan esas condiciones: por
ejemplo invirtiendo a y c en la figura, obtenemos: la figura actual ( a la
izquierda), con la codificación:
RED 8 Recto: H [çacç: 4] Oblicuo: X [çcaaç:
5]
que ya no es periódica en todas direcciones.
¿Qué falta?.
Se observa en este caso cómo las diagonales
no llegan juntas a la periferia (en rojo). Para que eso ocurra cada diagonal
debe comportarse como un rayo de luz que se refleja (con inclinación de 45º
en esta red de 8) en esa periferia, lo que se justifica en
Redes periodicas de 8. Allí
vemos que ello sólo sucede cuando la codificación de la
semisecuencia
oblicua es
capicúa
Ley 2
La recta no influye, es paralela a la periferia y por lo tanto
siempre coinciden esas rectas al trasladar y copiar de arriba y abajo y
hacia los lados el bloque de red. que representamos rodeado de rojo en las
figuras.
Si cumplimos las leyes así encontradas (empíricamente, es verdad) tenemos
una guía segura para dibujar redes de 8 periódicas. Un ejemplo:
RED 8 Recto: H [çacaç: 5] Oblicuo: X [çacccaç: 7]
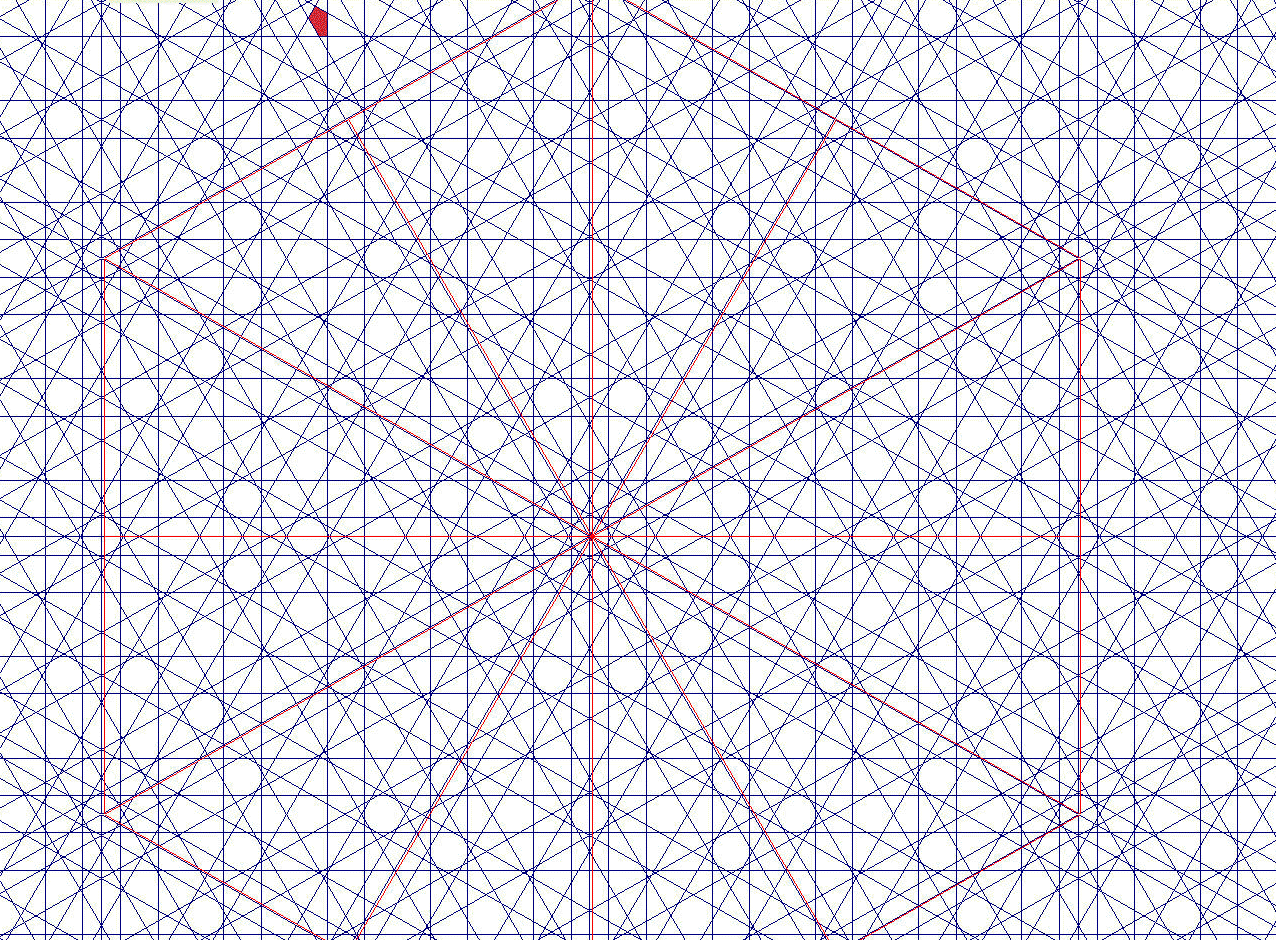
Simetrías
Si además queremos figuras simétricas respecto a varios ejes
‒generalmente paralelos a las direcciones principales‒ tenemos que
disponer las distancias anteriores de modo también simétrico.
Esto nos conduce a desechar algunas de las combinaciones posible que no
lo son. Las que quedan son del tipo
[ cuc ] = inv [ cuc ]
(3)
como las frases capicúa del tipo 'lava la bala' o 'daba la zorra arroz al
abad'. Así nos quedan las formas
X [ c a c] -H [ c a c]
X [ c c a.c c ] -H [ a c a]
X [ c c a. c c ] -H [ a c c a]
X [ c c a.a c c ] -H [ c a a c]
en las que comprobamos que se cumplen
rigurosamente las leyes (1) y (2)
....
Vuelta al Principio Última
actualización:
domingo, 12 de agosto de 2018 Visitantes:
