Redes periódicas de 8 (perteneciente a Decoración Geométrica Islámica)
En nuestro Diseño de redes de 8 hemos visto empíricamente las condiciones que deben cumplir las semisecuencias que definen el bloque de red para que al repetirse por translaciones vertical y horizontal se genere una red única en la que todos los bloques quedan colocados, es decir, sus rectas de red coinciden con las de la red general.
Veamos en detalle la justificación de esas reglas, una en realidad:
la semisecuencia oblicua debe ser capicúa
como la de la figura, que es: X [//çaacaaç:
7]: . Siete elementos pues, siete distancias que podemos ver en la figura.
En ella encontramos los puntos A, B y C en la periferia ‒en rojo.‒ vertical derecha del bloque de red.
Vemos que en esos puntos concurre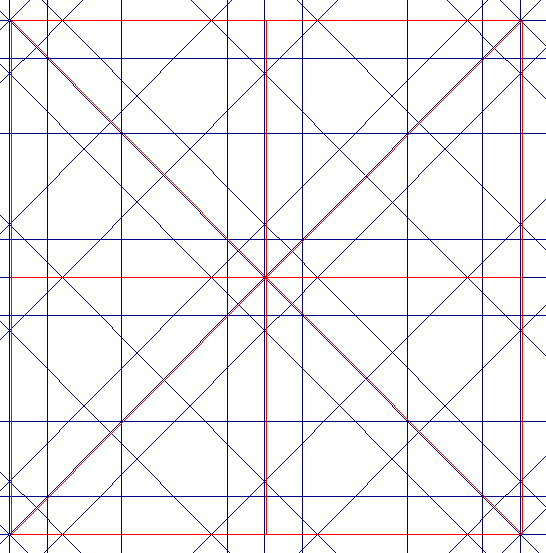n,
son generados por, dos rectas oblicuas con ángulos de 45º y 135º. Su
ordenación desde sus ejes de simetría , escritos dentro son
A, 6 - 1 B, 5 - 2 C, 4 - 3
o sea suman en todos los casos 7, la longitud de la semisecuencia.
Geométricamente eso significa que las suma de los segmentos de cada par
de rectas dentro del bloque es constante, o, lo que que equivale, también es
constante la suma de los segmentos concurrentes dentro del triángulo en rojo
limitado por la horizontal central, diagonal de 45º y la vertical a la
derecha, lo que llamamos elemento generador de red. Nombre justificado
porque por simetrías repetidas respecto a los ejes de simetría, en rojo, qu
no pertenecen a la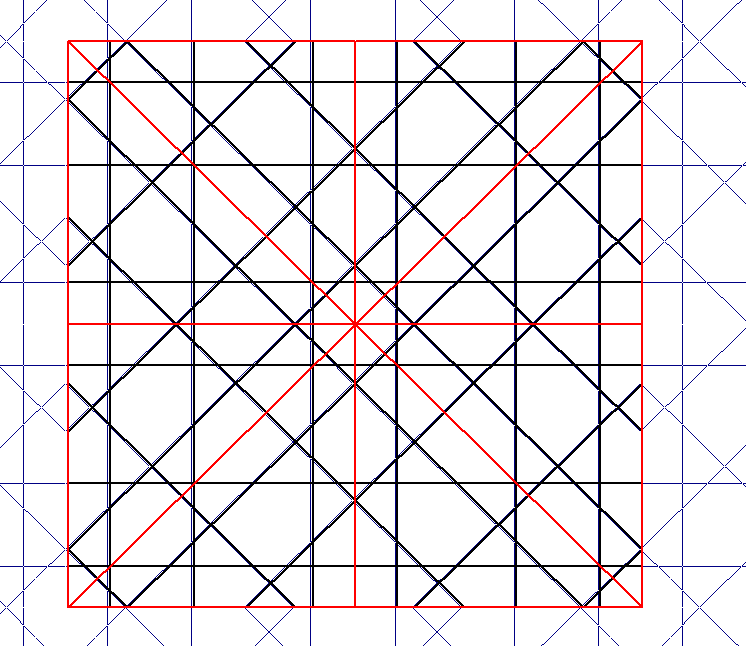
red, se ge
RED 8 Recto: H [çacç: 4] Oblicuo: X [çcaaç: 5]
La situación se repite en el triángulo simétrico al generador respecto a la bisectriz principal, con los puntos homólogos A', B', C' y en los demás simétricos con los tríos A",B",C";A"', B"', C"' y así sucesivamente hasta 8 veces..
La no constancia de esa suma, igual a la longitid de la semibisectriz principal, conduce al caso 3º, en que la red interior no genera la exterior.
Se ven estas redes periódicas en Catálogo de redes 8.y se compriuba en todas el cumplimiento de la condición encontrada.
Vuelta al Principio Última
actualización:
viernes, 18 de septiembre de 2015 Visitantes: