Diseño general de redes (perteneciente a Decoración Geométrica Islámica)
A partir del diseño individual de redes, para 6, 10, 12 y otros, resumimops aqui el caso general:
Análisis de redes
He aquí nuestro análisis informático de la calidad periódica de una red según su ordem N
Select Case 2 * n
Case 8:
If g(1) Mod 2 <> 0 Then text1Text = text1Text + " Num. de 'c' en oblicuo ha de ser par"
If b(1) <> g(0) Then text1Text = text1Text + " Num. de 'a' en oblicuo ha de ser igual a Num. de 'c' en recto"
If g(1) <> 2 * b(0) Then text1Text = text1Text + " Num. de 'c' en oblicuo ha de ser doble que Num. de 'a' en recto"
bg = b(0) + b(1) + g(0) + g(1):
If Int(bg) <> bg Then text1Text = text1Text + " Num.s de 'c' y 'a' en oblicuo y en recto han dese todos enteros"
desigual = 0
For ii% = 1 To semisecuencia(0, 1) / 2
If semisecuencia(ii%, 1) <> semisecuencia(semisecuencia(0, 1) + 1 - ii%, 1) Then desigual = 1
Next
If desigual = 1 Then text1Text = text1Text + " Ss oblicua no es capicúa."
Case 12:
If g(1) Mod 2 <> 0 Then text1Text = text1Text + " Num de 'c' en oblicuo ha de ser par"
If b(1) Mod 2 <> 0 Then text1Text = text1Text + " Num de 'a' en oblicuo ha de ser par"
If 3 * b(1) <> 2 * g(0) Then text1Text = text1Text + " Num de 'a' en oblicuo ha de ser tres medios de Num de 'c' en recto"
If g(1) <> 2 * b(0) Then text1Text = text1Text + " Num de 'c' en oblicuo ha de ser doble que Num de 'a' en recto"
bg = b(0) + b(1) + g(0) + g(1):
If Int(bg) <> bg Then text1Text = text1Text + " Nums de 'c' y 'a' en oblicuo y en recto han dese todos enteros"
For kk% = 0 To 1 'semisecuencia(0, kk%) / 2
desigual = 0
For ii% = 1 To semisecuencia(0, kk%) / 2
If semisecuencia(ii%, kk%) <> semisecuencia(semisecuencia(0, kk%) + 1 - ii%, kk%) Then
desigual = 1
text1Text = text1Text + " Ss " + Str(kk%) + " no es capicúa."
End If
Next
Next
'X doble capicua
'busco solo en la cuarta parte
desigual = 0
kk% = 1
For ii% = 2 To semisecuencia(0, kk%) / 4
If semisecuencia(ii%, kk%) <> semisecuencia((semisecuencia(0, kk%) + 1) / 2 + 1 - ii%, kk%) Then
desigual = 1
text1Text = text1Text + " Semisecuencia " + Str(kk%) + " no es doble capicúa."
End If
Next
Case 10:
text1Text = text1Text + " No ACTUALIZADO"
If g(1) Mod 2 <> 0 Then text1Text = text1Text + " Num de 'c' en oblicuo ha de ser par"
If b(1) Mod 2 <> 0 Then text1Text = text1Text + " Num de 'a' en oblicuo ha de ser par"
If b(1) <> 2 * g(0) Then text1Text = text1Text + " Num de 'a' en oblicuo ha de ser doble que Num de 'c' en recto"
If g(1) <> 2 * b(0) Then text1Text = text1Text + " Num de 'c' en oblicuo ha de ser doble que Num de 'a' en recto"
bg = b(0) + b(1) + g(0) + g(1):
If Int(bg) <> bg Then text1Text = text1Text + " Nums de 'c' y 'a' en oblicuo y en recto han dese todos enteros"
desigual = 0
For ii% = 1 To semisecuencia(0, 0) / 2
If semisecuencia(ii%, 1) <> semisecuencia(semisecuencia(0, 1) + 1 - ii%, 1) Then desigual = 1
Next
If desigual = 1 Then text1Text = text1Text + " Ss oblicua no es capicúa."
Ya en nuestro artículo a_model_of_islamic_rectilinear_interlaced lattices mostrábanse las relaciones entre orden de la red (número de direcciones-sentidos de una figura, y las distancias entre rectas paralelas a esas direcciones.
Orden y distancias
Se ofrecía una relación entre esas distancias cuando eran sólo dos, caso típico y además estético. Esa relación era y es
a/c =2.cos(360º/N), o en radianes a/c =2.cos(2p / N) a/c = 2.cos(p /n)
siendo a y c esas dos distancias, N el número de radios paralelos a esas direcciones y n su mitad, cuando como es habitual N es par.
Así que para una división de la circunferencia en 8 partes, red o lazo de 8, N=8, n=4, a/c=√2 =1.4142..
Así que en toda red de 8 usaremos distancias iguales a una de esas dos, Si c=1 , a= 1.4142.
Ahora bien, hay que determinar varios
parámetros adicionales para diseñar una red concreta que cumpla con otras
condiciones opcionales, también adicionales.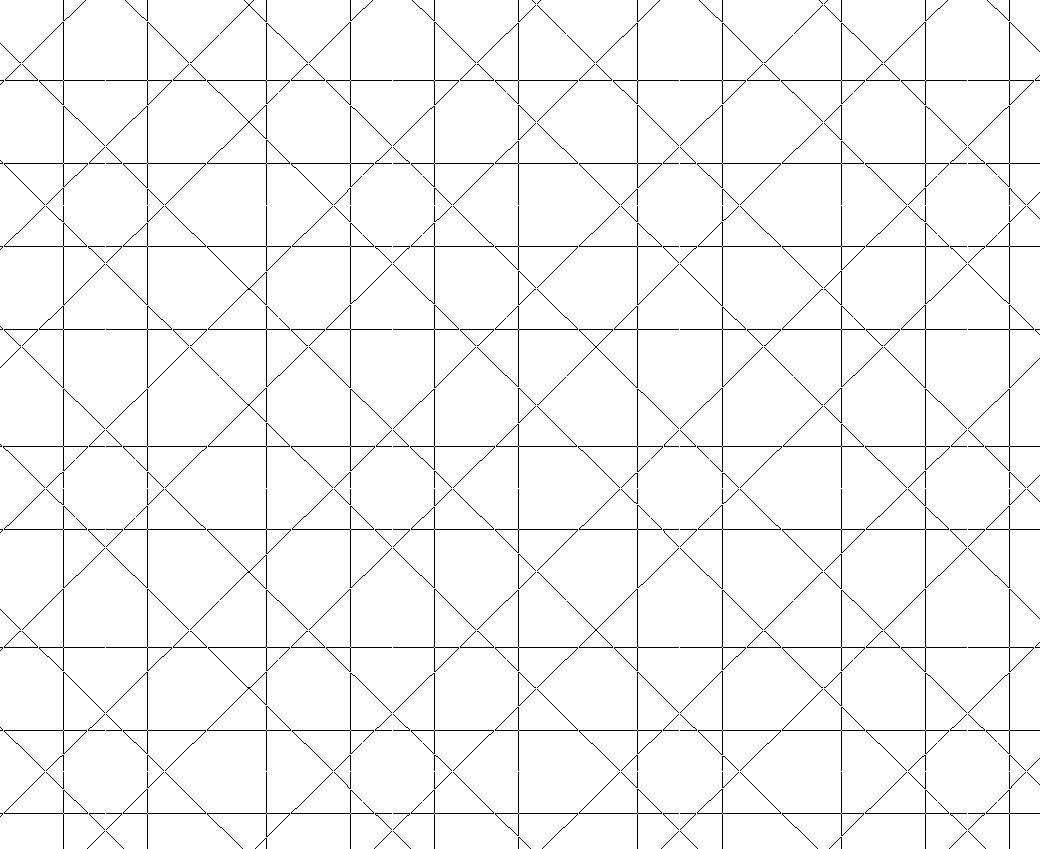
La primera condición es la periodicidad de la red, es decir, que las distancias entre rectas forman un patrón que se repite periódicamente. Esto es indispensable, pero la estética largamente ensayada de estas figuras lo hace muy a menudo, llegando así a figuras que se repiten asimismo en varias direcciones. Esto tiene que ver con el retorno rítmico de sucesos, aquí, visuales. Esas periodicidades y coincidencias a intervalos regulares en las dos dimensiones del dibujo dan lugar a poligonales y Riges, también periódicamente repetidas, y a poligonitos simétricos, generalmente.
Se consigue esta periodicidad haciendo que los grupos de distancias en direcciones contiguas incluyan combinaciones de 'a' y 'c' tales, que coincidan en un triángulo. Por ejemplo, en la red de la figura, muy común y fecunda aunque simple, observamos que las verticales y horizontales se repiten con regularidad, en una secuencia infinita de distancias:
...a, c, c, c, a, c, a, c, c, c, a...
es decir con un periodo, cuyo comienzo elegimos arbitrariamente (cualquiera vale en una secuencia periódica): [c.a.c.c.c a]. mientras que las oblicuas se disponen en la secuencia:
a, c, a, c, a, c,...
es decir con un periodo [c.a]. (o [a c].) .
Los comienzos de ambas series son arbitrarios pero están ligados en ambas secuencias: es decir, deben coincidir ambas series en ese comienzo. Así tenemos el par de periodos emparejados: en rojo: : [c a.c a] // [c a.c a] .
En general tenemos que recordar las dos fórmulas básicas de la red de 8:
1) que la hipotenusa se proyecta en un cateto. y
2) que dos catetos seguidos se proyectan en una huipotenusa.
Si el cateto es 1,
2 · cos(45º) = 2 · (√ 2 / 2) = √2
de modo que, si usamos el apóstrofe para significar 'proyectado' (ángulo de 45º) tenemos
a'= c (2c)'= a (1)
o sea, que una combinación de distancias acumulada de [ba+2gc] se proyecta como [ga+bc]. Esta comprobación determina si en efecto esas combinaciones, en cualquioer orden, forman un triángulo generador apropiado.
[ ba+2gc ] ' = [ ga+bc ]. (2)
De modo que toda combinación de a y c en diagonal sufrirá esa transformación en la proyección. Así nos obliga a
tener siempre una combinación par de c en las diagonales.
Veamos combinaciones posibles
X [a] H [c] . X [c c] H [ a] . X [a c c] H [ c a] y también. X [c a c] H [ a c] . X [c c a]H [ a c] , es decir permutaciones al azar de los segmentos requeridos. X [c a c] H [ ac] . y sus permutaciones X [a a c c] H [ c c a ] y sus permutaciones X [a a c a c]-H [ c c c a ] y sus permutaciones
y así sucesivamente.
Recuérdese que los ejes de simetría, en rojo, a a partir de los cuales se miden las distancias, no pertenecen a la red, solo la ordenan y marcan simetrías.. De igual manera que el espejo no pertenece ni al espacio original ni al reflejado. O el guarda, que organiza la circulación, pero no circula.
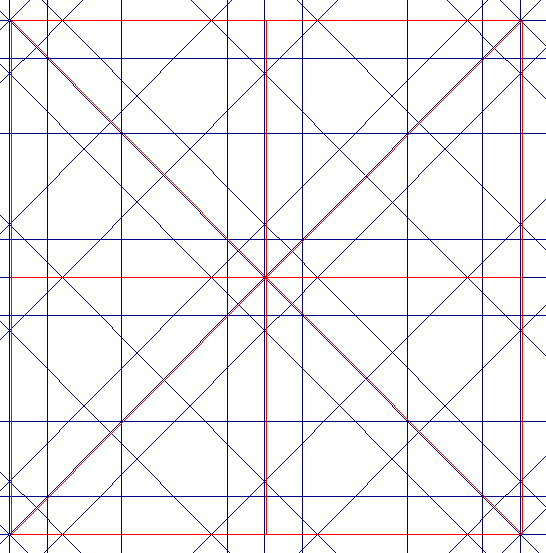
Sin embargo, no bastan esas condiciones: por ejemplo invirtiendo a y c en la figura, obtenemos: la figura actual ( a la izquierda), con la codificación:
RED 8 Recto: H [çacç: 4] Oblicuo: X [çcaaç: 5]
que ya no es periódica en todas direcciones. ¿Qué falta?.
Se observa en este caso cómo las diagonales no llegan juntas a la periferia (en rojo). Para que eso ocurra cada diagonal debe comportarse como un rayo de luz que se refleja (con inclinación de 45º en esta red de 8) en esa periferia, lo que se justifica en Redes periodicas de 8. Allí vemos que ello sólo sucede cuando la codificación de la
semisecuencia oblicua es capicúa
La recta no influye, es paralela a la periferia y por lo tanto siempre coinciden esas rectas al trasladar y copiar de arriba y abajo y hacia los lados el bloque de red. que representamos rodeado de rojo en las figuras.
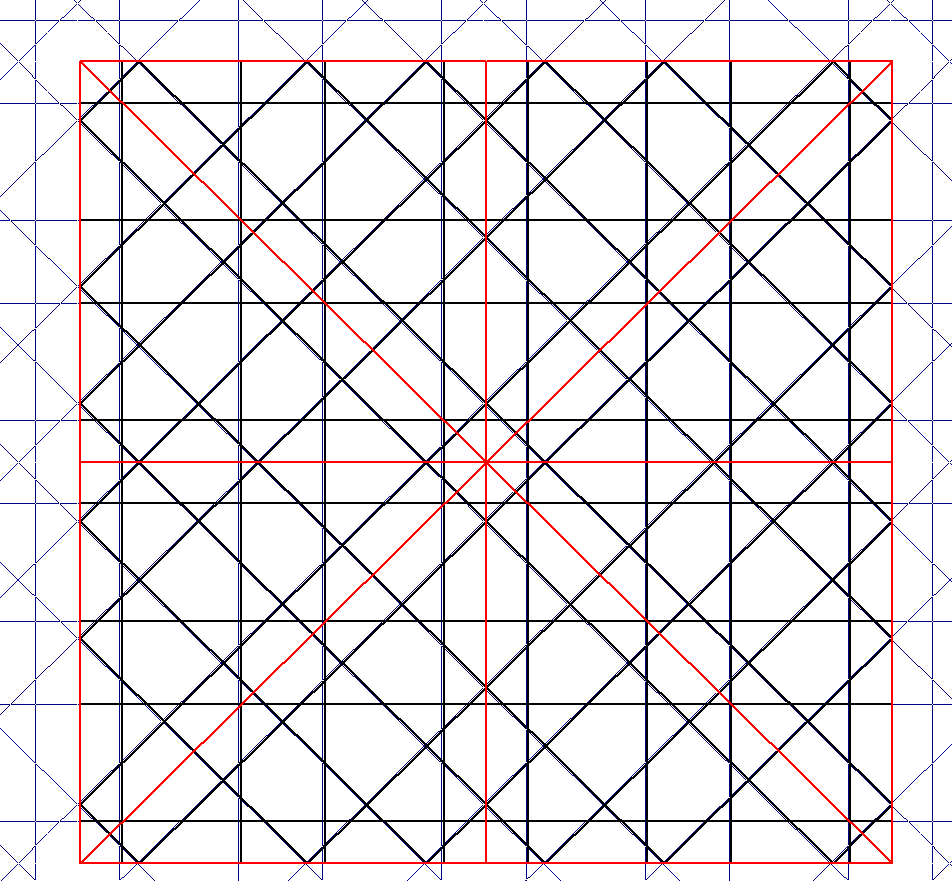
Si cumplimos las leyes así encontradas (empíricamente, es verdad) tenemos una guía segura para dibujar redes de 8 periódicas. Un ejemplo:
RED 8 Recto: H [çacaç: 5] Oblicuo: X [çacccaç: 7]
Simetrías
Si además queremos figuras simétricas respecto a varios ejes ‒generalmente paralelos a las direcciones principales‒ tenemos que disponer las distancias anteriores de modo también simétrico.
Esto nos conduce a desechar algunas de las combinaciones posible que no lo son. Las que quedan son del tipo
[ cuc ] = inv [ cuc ] (3)
como las frases capicúa del tipo 'lava la bala' o 'daba la zorra arroz al abad'. Así nos quedan las formas
X [ c a c] -H [ c a c]
X [ c c a.c c ] -H [ a c a]
X [ c c a. c c ] -H [ a c c a]
X [ c c a.a c c ] -H [ c a a c]
en las que comprobamos que se cumplen rigurosamente las leyes (1) y (2) ....
Descentrado
Hay más condiciones: si queremos que las rectas de la red se crucen dos a dos, debemos descentrar las rectas, es decir, evitar que coincidan con los ejes de simetría. Para ello desplazamos esas rectas la mitad de una de las distancias.
Si elegimos 'c' como la distancia partida, y llamamos a esta mitad 'ç' entonces obtenemos de las soluciones anteriores las siguientes:
x [ ç a c ç] -H [ ç c a ç]
y vemos que ya no es capicúa.
Las condiciones se han endurecido: ahora debe haber un número par de c en la serie oblicua, porque cada pareja deviene 'a'.
La condición de capicúa obliga a que el número de 'a' (que devienen 'c' cada una al proyectar) sea igual al de a, porque al proyectar devienen un número.
Su además deseamos calles en los extremos del periodo, o sea, medio c, 'ç' en ellos, esto nos obliga además:
Ls ç de los extremos de la sucesión en cruz (-H) nos requiere otro c
Rehacemos los cálculos y obtenemos el siguiente valor mínimo simétrico, descentrado y capicúa:
X [ ç c a c a c ç ] -H [ ç a c a ç ] (4)
que cumple
[ ç c a c a c ç ] ' = [ c c c c a a ] ' = [ c c] ' + [ c c] ' + [ a a ] ' = [a] +[a] + [c c] = [ ç a c a ç ]
Nótese que encontramos un valor obligado c, una calle en el centro de cada una de las series, siempre teniendo en cuanta que henos obligado a media calle en los extremos.
Este valor mínimo puede ampliarse de modo que se sigan conservando todas las condiciones; para ello añadimos siempre un valor par de a en oblicuos (que pasan a rectos como par de c), o cuádruple de c (que pasan como un par de a). Veamos ambos casos:
X [ ç a c a c a c a ç ] -H [ ç c a c a c ç ]
añadiendo 2a cerca de los extremos del oblicuo y 2c cerca de los extremos del recto. O bien:
X [ ç c a a c a a c ç ] -H [ ç c a c a c ç ]
añadiendo 2a cerca del centro del oblicuo y 2c cerca de los extremos del recto. Cabe cualquier combinación en cada una de las series rectas y oblicuas, pero siempre conservando la simetría respecto al centro en cada una. Así que simbolizamos esa libertad poniendo entre paréntesis la zona permutable, reflejada en un paréntesis simétrico en la otra. Así las cuatro posibilidades apuntadas quedan reflejadas en el esquema:
X [ ç ( a c a ) c ( a c a ) ç ] -H [ ç ( c a) c ( a c ) ç ]
Nótense las simetrías de esos paréntesis respecto al c central de cada secuencia. La permutación es libre en cada serie: es decir permutamos la parte libre de las oblicuas con independencia de la permutación en las rectas. La repercusión de una u otra elección consiste en una mayor coincidencia de vértices en la red consiguiente. Ya veremos esto en la práctica.
Para resumir aún más, podemos escribir sólo la mitad del capicúa, recordando que el c central es independiente e inamovible.
X [ / c / ( a c a ) ç ] -H [ / c / ( a c ) ç ]
donde la barra inclinadas rodeando al c central indican que la parte a su derecha ha de copiarse en espejo a la izquierda de la otra.
El caso mínimo es
X [ / c / (a c) ç ] -H [ / c /(a) ç ]
que podemos recodificar más concretamente como
X [ // ç (a c) ç ] -H [// ç (a) ç ] (5)
que interpretamos como: la semisecuencia a la derecha de las dos barras inclinadas (slash) la copiamos en espejo, en reflejo a la izquierda. Esta codificación la llamamos el par de semisucesiones mínimas o generatrices, ya que contienen toda la información necesaria para generar la red en forma mínima o condensada del todo.
Las permutaciones dentro de los paréntesis nos permiten dos posibilidades en las series oblicuas.
X [ // ç a c ç ] -H [ // ç a ç ] y X [ // ç c a ç ] -H [ // ç a ç ]
Ahora podemos comprobar que la red de la figura es una de las disposiciones de la mínima, precisamente la primera:
X [ ç a c a (çç) a c a ç ] -H [ ç c a (çç) a c ç ]
que se reparte a cada lado de la simetría central dividiendo el dos la calle (c) central, en dos mitades o semicalles (ç):
X [ ç a c a (ç ç) a c a ç ] -H [ ç c a (ç ç) a c ç ]
Al prolongar este períodos indefinidamente se obtiene la serie que encontrábamos empíricamente al principio:
X [ ... c a c a c a c a c a c a c... ] -H [ ... c c c a c a c c c a c a c c c a c a c c c ... ]
pero ahora sabemos mucho más. Podemos general indefinidamente redes más y más complicadas.
Como decía el sabio oriental 'primero estaba la montaña, después no hubo montaña y al final hubo montaña'.
Nos queda ahora otro escollo no obstante lo mucho avanzado:
No todas las redes así generadas forman una red periódica en todos los sentidos. Por ejemplo, veamos la red de la figura, que corresponde a un caso real, es decir, encontrado en algún edificio tradicional.
Veamos otro caso, más complicado, el definido en nuestra notación por:
R8: X [ á c a c a c c a c a c á:12]-H[á c c a c a c c á:9]
Se observa la simetría especular de la semisucesión, es decir, es capicúa a su vez. La sección a cada mitad del eje de simetría del Bloque de Translación, cada cuadrante en este caso es a su vez simétrico en las distancias y por lo tanto simétrico en la figura: cada cuadrante admite ejes de simetría centrales.
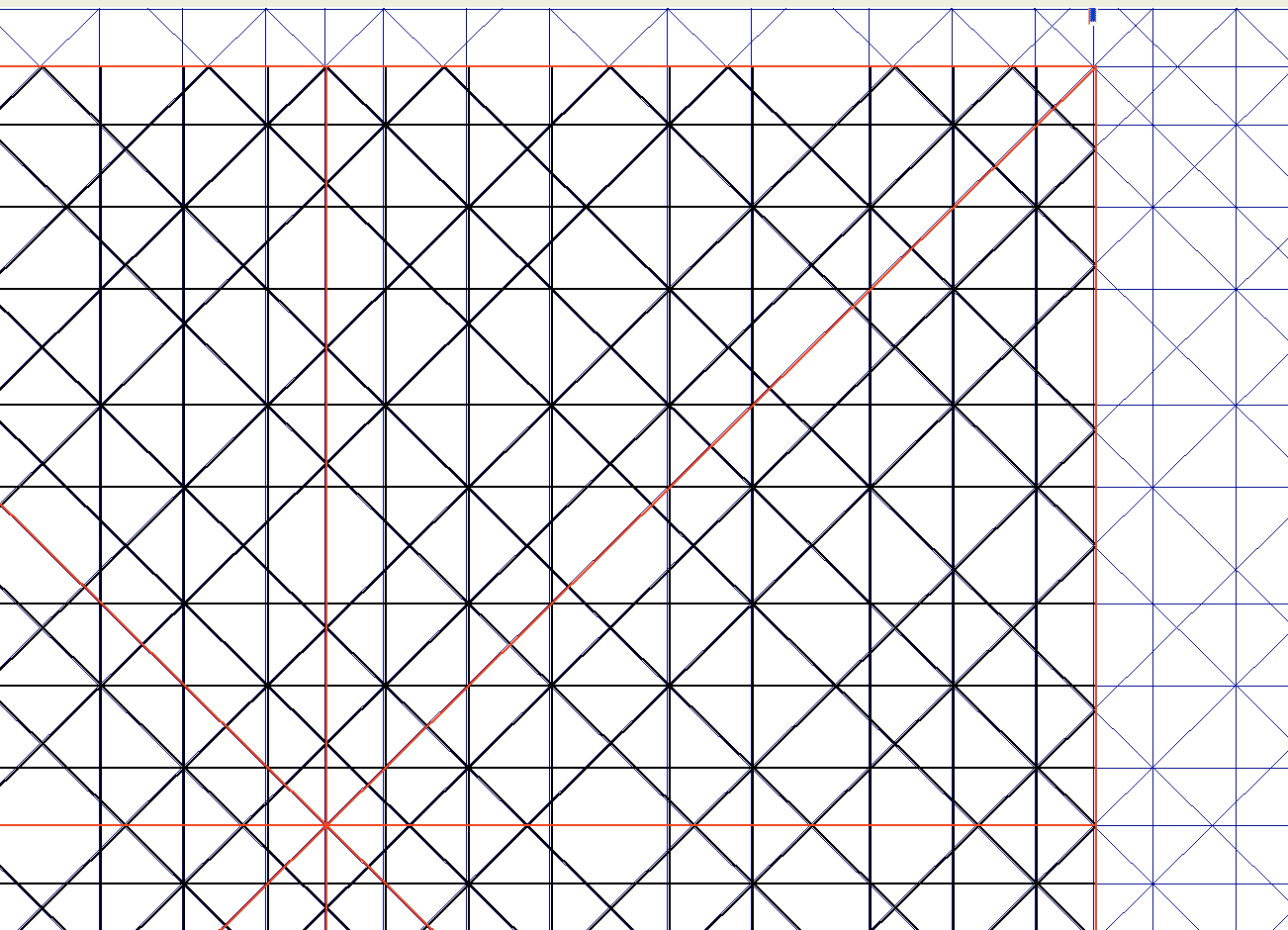
La novedad reside aquí en que en lugar de colocar semicalles en los límites de las sucesiones y semisucesiones de anchura menor, la llamada 'c' en esta se usan semicalles de la mayor, 'a'.
Nótense que se cumplen las condiciones (1): y (2) :
X ' = H , o sea [ á c a c a c c a c a c á]' <> [ 5a 6c] ' = [ 5c 3a] <> [ á c c a c a c c á]
L a red anterior se usa como fondo o textura en unos azulejos de la mezquita del viernes, en Isfahan. Se estudia en lacework_analysis.
Hay que recordar sin embargo, que esta simetría de la semisucesión que produce la red infinitamente periódica es sólo una elección: si no se desea esa infinitud, una red de semisucesión no periódica (si la sucesión) es elegible.
Sumarizamos las leyes empíricas encontradas, suficientes para obtener una infinidad de redes de 8 periódicas en todos los sentidos.
1. Coeficientes de las combinaciones lineales de a y c en oblicuo X y recto H cumplen:
X[ ba+2gc ] ' = H[ ga+bc ]. (1)
2. X es capicúa:
X[ i ] = X[ loX - i ]. (2)
siendo loX la longitud de la semisecuencia oblicua X.
Insertamos estas condiciones en nuestro programa PUERTRA, lo que nos permite obtener y dibujar fácilmente estas redes.
Con los resultados elaboramos un catálogo de redes de 8, virtualmente infinito, ya que ofrecemos los primeros o más sencillos casos y una regla para ampliaros indefinidamente. Se justifica todo esto con más rigor en Redes periódicas de 8
y se vr el resultado en Catálogo de redes 8.
Vuelta al Principio Última
actualización:
viernes, 18 de septiembre de 2015 Visitantes: