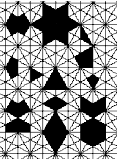
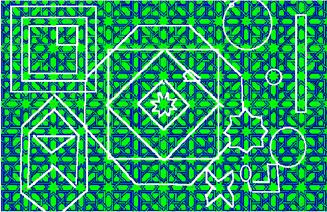
Esta página está en construcción: perdonen los errores y temas inacabados.
This page is being developed: I am sorry for errors and unfinished subjects.
A Model of Islamic Rectilinear Interlaced Lattices
ABSTRACT. The software package PUERTRA implements a theoretical study of formal properties of Islamic Geometrical Art, found extensively in wood work (artesonado ceilings, mosque minbars, doors and windows, inlay furniture), ceramic tiles (court yards, cupola roofs), wrought iron, stucco relieves, tapestry, and many other cases, in the Islamic World, past and present, specially in Al‑Andalus and later in Spanish Mudejar art. This theory is applied to the design and drawing of these intricate and beautiful forms, allowing the user to choose and try out colour schemes, polygonal order, interlaced frames, relative sizes, position, etc. Every formal aspect of the design is controlled, and can be recovered as a tool for use in manual or automatic manufacture and design, in Fine Arts, Arquitecture and Arqueology studies, and Form research.
INTRODUCTION
We examine in this paper what may be termed Islamic Geometric Art, however it is also found in other religions, such as Jewish and Christian, Eastern (Syriac, Coptic) and Western (Mudejar Art, from Al-Andalus, Spain). Earlier forms can be seen in Roman and Byzantine Art, as well. But its main development is related to Islam, in Al‑Andalus, Maghreb, Egypt, Turkey, Persia, Afghanistan, Pakistan and Islamic India. See references [Audsley,1968. Bourgoin, 1973. Bourgoin, 1977. Burckhardt, 1972 and 1976. Cabanelas, 1988. Critchlow, 1992. Grabar, 1984. Jawad al-Janab, 1982. Martínez, 1976. Nuere, 1989. Ögel,1987. Pavón Maldonado, 1981, 1990. Prieto y Vives, 1977. Sánchez, 1993-a. Sánchez, 1993-b. Speltz, 1959. Wilson, 1988.].
We will focus on a particular but representative branch of this geometric art: the Rectilinear Lace, which we will call Rige ("Red Islámica Geométrica Entrelazada"/ islamic interlaced geometrical lattice). We shall try to find the formal parameters which define this branch, and therefore separate it from other modalities of decoration, existing or possible. Of course, we do not intend to exhaust this intricate matter, nor explain everything about it; we are only raising a number of questions and begin to answer them, showing perhaps ways to follow on with a further study. Our experience is that, the more one draws designs and thinks about them, the more beautiful possibilities and properties are brought to light, giving a strong basís and unity to that branch of the Islamic Decorative Arts (in Arabic, zákhrafa ) [Cabanelas, 1988. Prieto y Vives, 1977. Nuere, 1989.].
Hence we shall not deal with historical considerations and cultural heritages. Only a few metaphysical remarks will be made; it could not be otherwise, given the strong numerical and symbolic aroma which pervades this particular form of art.
First, we shall propose a set of axiomatic formal rules which model, in our opinion, those forms. Afterwards, we shall develop, comment, even contradict, those rules, showing the relation between geometry and art.
FORMAL RULES
We formally characterize the Rectilinear Lace by means of the following restrictions or rules for the Rige forms:
R0. A Rige is developed in two dimensions, however, reliefs and holes are used to mark the designs.
R1. Only figures limited by straight segments are considered. Curvilinear design can be used to fill elementary polygonal figures, to avoid rigidity, dryness and too geometrical forms. But they do not contradict the basic rectilinear criterion, which remains.
R2. All these segments are parallel to a few directions in the plane, derived from the division of the compáss (360 degrees) by an integer N. This integer is called the Order, and the N directions, the main directions. Direction 0 will be the Reference, and 2=360º/N will be called the Basic Angle. Violations of this rule are exceptional, and will be considered in the Metabolê section below. They do not, however, affect this very basic law.
R3. All these segments are situated on specific straight lines, parallel to the main directions. The distances between those lines are always equal to a very small number of quantities, 1, 2 or 3, according to the order. These distances are not arbitrary, but are determined by this order and by the angles - all multiples of 2 - between the main directions.
R4. The set of the N families of parallel straights is called the Lattice or Net of the form, briefly the N-lattice. All the segments belong to the Net; all the figures belong to the Net; the Net can be considered as the union or set of many possible Rige forms of a given order.
R5. The segments form closed polygonal figures, convex or not, symmetrical or not. Those without segments between them will be the Elementary Elements -EE- (elements in the lowest level), which, by juxtaposition, give larger figures.
R6. Their sizes are not too different: a general aspect of constant density of lines can be observed (and measured), recalling a grid, or a tissue.
R7. At least one point can be found which is a symmetry centre for all, or a part, of the form. The order of this central symmetry is equal to the order of the net to which the form belongs.
R8. The segments which limits the figures are united in polygonal lines with a width, as frames or sheets, which are never interrupted: whether they are closed or whether they finish in the external limits of the figure (actual figures are always limited, while nets are infinite by nature).
R9. The width of the frame is constant for the same form.
R10. When frames intersect, only two do so at the same point. The angle is non‑zero (and of course, equal to the angle between two main directions). Frames never bend at the intersection point, or, equivalently, opposite angles are equal.
R11. The intersection is usually represented (from Arabic countries to the West) as in three dimensions: one frame covers the other.
R12. When one frame (f1) covers another (f2) at a given intersection, at the following intersection it will be covered in turn by a third (f3) (which could be the second, f2).
R13. The form can actually be constructed by means of physical frames, bent and interlaced according to the former rules. Simple figures (EE) appear as empty spaces between frames.
R14. When the widths of frames are maxima, they fill the entire plane, with the disappearance of elementary figures. The aspect is now a polygonal chess board (damero), used in wood‑work, musical instrument decoration, etc.
ELEMENTARY FIGURES
Among all possible EE, the Rige tradition shows a preference for the symmetrical ones; for instance, in fig. 6 and 7, all the 10 EE are symmetrical, 8 with only 1 axis, 1 with 2, and 1, the star, with 8 axes, the maximum number for a 8-lattice. Note that those numbers are all divisors of N. See something more of this subject in the 'musical Relationship' paragraph.
The EE receives names according to its appearance: stars, barrels, candles, almonds, streets, diamonds, are names used in old times and nowadays [Jawad al-Janab, 1982., Nuere, 1989. Pavón Maldonado, 1981, 1990. Prieto y Vives, 1977.]. This attribution of thing names to abstract designs is not the smaller pleasure which Rige design offers, the possibilities being limited only by the intuition of the practitioner: new forms can appear after months of frequentation of a form. See some of these EE in fig.1 and 2.
Geometrically, the EE are polygons whose angles are multiple of the Basic Angle 2=360°/N degrees, 2B/N radians. The lower the order, the simpler the elementary figures. As the sum of the inner angles is equal to B×(n-2), n being the number of sides or angles, for the triangle ( n=3):
"+$+( = 180°, k 2+ k'2 + k"2 = B, ( k + k'+ k") × 2 = B,
( k + k'+ k")× 2B /N = B
and we obtain the interesting formula:
k + k'+ k" = N/2
Since k, k,' k" are integers, N must be even, which justifies the parity of the orders formerly considered, at least for triangles. Now, if we have an 8-lattice, N/2=4, and only one possibility remains:
k = k'= 1, k"=2
two 45° angles and one 90°, that is, an isosceles right angled triangle, as intuition would tell us. For a 10-lattice, two more combinations are possible, both isosceles: 1-1-3 and 1-2-2.
More quadrilaterals are possible. The formula now becomes
k + k'+ k" +k "' = N
In general, the number:
E k i = (n-2) × N/2 must be an integer.
In Table 1 some possible polygons - only the symmetric and convex ones - are listed, accompanied by the values of N and n.
LATTICE ORDER and DISTANCES
In theory, the order of a lattice could be any integer, but constructive, psychological, aesthetic and mathematical reasons limit its values to small numbers with many divisors. Typical cases are 8, 10, 16, 20, 24 and 32. The constructive reasons are (or were) the difficulty of making wood, plaster, ceramic pieces with extremely fine angles, and with too many possibilities: in a 36-lattice there may appear angles of 10, 20, 30, ... 350 degrees, 35 different values. The tools would have to have been very exact, which was not easy in medieval times. The psychological reasons relay on the difficulty in perceiving so many different angles and distances. This leads us to aesthetics: the sense of unity is lost as in an intricate and baroque relief. Some mathematical reasons can also be found, probably related to the former: the higher the order, the more polygons are possible and the lattice will need many different distances, complicating again the form for designer, maker and observer. Let us expand further this subject of distances between the straights of a family.
|
An 5-lattice and some elementary shapes |
If we do not impose any symmetrical rule, any distance is possible. But if we do, as Tradition demands, once we choose one, the gyration for central symmetry will create 'alias' in another radius, thus creating new distances as a necessity. Let us see some cases from the simplest to some more complicated ones.
ORDER 6. This is a very simple case. The angles are the 6 multiples of 2=360°/6=60° that is, 0º, 60º, 120º, 180º, 240º and 300º. If we consider a triangle, it must be equilateral, as shown before, and the angles will be 60º, 60º, 60º. If we choose any distance on the horizontal as a side, the same distance appears by rotating it on the oblique side, for equilateral. Thus we have only one distance necessary in the case N=6. We can use more, of course, but the order does not impose it, one is enough.
ORDER 8. A simple, but already interesting case. The angles are the 7 multiples of 2=360°/8=45°, that is, 45º, 90º, 135º, 180º, 225º, 270º and 315º. If we consider a triangle with angles 45º-45º-90º, once we gyrate the hypotenuse on the horizontal side, we obtain a new distance as a consequence of the first one. The ratio between them is %2/1 =%2. So the lattice order implies a specific distance ratio. See this ratio in Fig.1.
|
An 8-lattice and some elementary shapes |
Now the problem is to know how many different distances we need. If we raise another perpendicular to the horizontal at point %2, the new distance on the diagonal will be %2 ×%2 = 2. But this distance is 2 times 1, that is, a second distance equal to the first, 1: we do not need another distance in this case. In general, any gyration of a linear combination of these two distances, 1 and %2, will provide us with another combination of them: they form what is known as a Vector Space, with 1 and %2 as a Base of the Space:
(a+b%2) × %2 = 2b + a%2 = b' + a%2
ORDER 10. A very interesting and very beautiful case. The angles are the 10 multiples of 2=360/°10=36°, 0, 36, 72, 108, 144, 180 and its symmetric by the horizontal. A simple triangle will be the isosceles 36-72-72. Once the base of the triangle is chosen, the distances between parallels which appear now in the triangle are its heights. The ratio of its values are found to be, after little counting, 1.6180.... But this is a prestigious number, older than the civilizations about which we are talking: this is the Golden Proportion, considered as a very harmonic ratio of two distances (like a picture frame, for instance). Its exact value is (1+%5)/2; let us call it M. If now, we take another triangle with the smaller height equal to a linear combination of 1 and M, with coefficients a,b, the other one will be (a+bM)×M = aM+bMM. But
M×M =(1+%5)/2 × (1+%5)/2 = (1+5+2%5) / 4 = (3+%5) /2 = 1 + M
therefore
(a + b M) × M = aM + b(M×M) =aM + b(1+M) = b + (a+b) M = b + a'M
|
An 108-lattice and some elementary shapes |
what means that also the other height is a linear combination of 1 and M, and, again in this 10-space, the pair (1,M) is a base vector. For instance, in Fig.2, all the distances are equal to 1, M, 1-M or any other linear combination.
Beautiful and well-known relations can be found for this number M; see several developments of this subject in [Coxeter,1973. Ghica, 1977. Rademacher & Toeplitz,1970].
GENERAL CASE. As we have seen in the former cases, any order which engenders in other radii distances which can be expressed as a linear combination of two, will accept this pair as a base, and any linear combination of them, or what is equal, the distance between any two straights of the same series, will form a legal or permitted triangle (with vertices on some nodes of the lattice), using some other combinations of the base vectors.
If we try all the linear combinations of distances which determine a valid triangle in an N-lattice, we will arrive at the expression:
(ms × n ‑ m× ns) × (sin(") × mp ‑ sin($)× m) - (mp× n ‑ m× np) × (sin(")× ms ‑ sin(()× m) =0
where ", $, (, are the angles; (m, n), (ms, ns), (mp, np) are the coefficients of the linear combination of the two unknown base vectors for the distances between straights of the three series whose intersection generate this triangle. By trying different combinations with small values (otherwise the job will last an infinite time) we obtain two-vector bases whose ratios allow legal triangles, as we have shown individually for the 6, 8, and 10 cases.
Since any elemental figure (EE) of a Rige can be decomposed into triangles, the found basís also allows legal Rige, and therefore constitutes answers (not all, but some) to the question raised about the distances between straight series. In Table 1 we can see some of these answers. In it are also shown several possible polygons in each lattice, some of which were shown in Fig.1 and 2. The angles are expressed one by one or, when possible, as a multiple, for regular convex and star polygons. In Table 2 are listed base vector ratios for greater values of N, obtained by the former expression, which are also equal to the value 2 cos(p/n), deduced by simple geometric calculus.
TABLE 1. LATTICES and their ELEMENTARY FIGURES
| N 2 | a/b exact | n Eki | polygons | ||||||||||
| 6 60 | 1 1 | 3 3 | 1-1-1 | ||||||||||
| 4 9 | 1-22-3 | ||||||||||||
| 6 12 | 6×2 | ||||||||||||
| 8 45 | 1.414 %2 | 3 4 | 1-1-2 | ||||||||||
| 4 8 | 4×2 | 1-1-1-5 | 1-2-2-3 | ||||||||||
| 6 16 | 11-22-33 | 2×(2-3-3) | 22-3333 | 11-333-5 | |||||||||
| 8 24 | 6×3 | 4×(1-5) | |||||||||||
| 16 56 | 8×(1-6) | 8×(2-5) | |||||||||||
| 10 36 | 1.618 M | 3 5 | 1-2-2 | 1-1-3 | |||||||||
| 4 10 | 22-33 | 2-3-2-3 | 111-7 | 1-333 | |||||||||
| 6 20 | 3333-44 | ||||||||||||
| 8 30 | 12222-777 | ... | |||||||||||
| 10 40 | 10×4 | ... | |||||||||||
| 20 90 | 10×(1-8) | .... | |||||||||||
TABLE 2. N-LATTICE RATIO
| N | a/b = 2cos(p/n) | a/b exact |
| 6 | 1 | 1 |
| 8 | 1.4142.... | %2 / 2 |
| 10 | 1.6180 ... | (%5+1)/2 |
| 12 | 1.7320... | %3 |
| 14 | 1.8019... | |
| 16 | 1.8477... | |
| 18 | 1.8793... | |
| 20 | 1.9021 | |
| 22 | 1.9189... |
PERIODIC and APERIODIC LATTICES
The set of distances that define the lattice with the order N, can be periodic or not. The first option is the most usual, because periodic repetition of distances allows periodic repetition of forms. But aperiodic lattices are also possible, as the 5-lattice of Penrose which never repeats a distance pattern. Periodic lattices are suitable for plane covering, while the aperiodic are better used in single forms (however the former can also cover planes, as the Penrose's). See in Fig 1 and 2 for respective examples of both kinds of lattice: in Fig.1, the 8-lattice uses two regular distance sequences, used in an alternate way according to the angle of the series (let %2 be called D):
...-1-D-1-D-1-D-1-D-... and ..1-D-1-1-D-1-1-D-1-D-1-1-D-1-1-D-..
meanwhile in Fig.2. the sequences are (let M' be 1-M = .618..):
... -M-1-M'-1-M-1- M'-... and .. -M'-1-1-M'-1-M-1-M'-...
are no longer periodic. But these are arbitrary examples, other lattices could be used for both orders with different periodic character.
SYMMETRIC ROTATION
The vast majority of Rige forms present regular symmetries which focus the attention on their centres and axes (see some aesthetic conclusions of this in musical Relationship, below). We consider two main kinds of these symmetries, central and axial. The first constitutes 'natural' centres, as the order of this symmetry becomes greater; the maximum value of it is N, the lattice order. Secondary centres are those with divisor symmetry, that is, with symmetry order a submultiple of N: in 10-lattice, the main centre has 10 order symmetry, and 5-order the secondary ones (Fig.12-13, Puertra, in Ap.1). There is only one case left, the 2-order central symmetry, not to be confused with the axial one. See this last case in the form Mevlüt, Fig.8.
The axial symmetries are easier to find, since they impose fewer conditions of similarity between parts of the form. In fact, there is a tendency to consider this symmetry as a must for every Rige, at least in the EE, as we have seen. The symmetry facilitates not only the comprehension of a form, but also its definition and construction, as we shall now show. Only a single part needs to be defined, since the other can be found by symmetrical repetition. This leads us to search for the minimal part of a Rige that can generate the rest in this way. If it can be found, we will call it the Generative Element (GE) of this particular Rige.
There is also a third type of symmetry in Riges, a faked spatial (3-dimensional) one: when interlace is adopted (see the paragraph that follows) the axial symmetry presents an alternative up and down (above/below) frame crossing which can be seen and understood as a spatial axial symmetry. The ideal procedure would then be to gyrate the GE round its symmetry axes, not in the plane, but rather in the space, as a door which emerges from the plane, and return to it after a 180 degree turn. This spatial procedure agrees with the psychological impression which interlace suggests: the Rige escapes from the plane to which it belongs and acquires depth, relief, spatial existence.
DISPLACEMENT PLANE COVERING
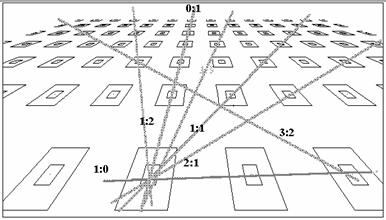
In periodic lattices, it is often found that parts of the form repeat themselves on the plane by translation (displacement) in two dimensions, until they cover the plane, or a part of it. This kind of repetition is suitable for actually covering big surfaces in a sort of trellis or canvas. See Fig.9-11, Alcazar, whose original covers the inner Patio of the Alcazar of Seville.
To carry out this translation, a new element must also be found and defined: the Translation Element (TE) of the form. This constitutes a usual type of decorative procedure, sometimes actually realized in physical form, such as the wood block that Indian tinters use to cover a silk cloth. The relative situation of the repeated TE must also be defined: when TE is rectangular, its repetitions can be situated in columns and rows; or in displaced rows, like bricks in a wall. Other shapes of TE would need a different disposition to cover the plane, like the hexagon, in a bee-panel pattern; see, again, [Coxeter, 1973. Ghica, 1977. Rademacher & Toeplitz, 1970.].
INTERLACE
The interlace is a nonessential feature for the Rige geometry, and in the eastern countries (from Persia onwards) does not appear. However it is common in the Arabic countries and was in the Spanish Al-Andalus and afterwards, in Christian commissioned Mudejar art (XIII- XVI cent.).
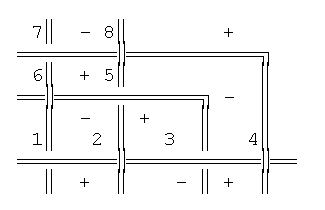 |
| Schema 1. Interlace and gyration sense. |
The universal way to achieve this interlace consists in passing the frame alternatively up and down the frames which it crosses. This system always has a solution, it is always possible to interlace frames in an alternative up-down basís.
Indeed, if we consider the polygons limited by the frames, we see that their sides are always segments of frames between two crosses, or, if the frame bends, the fragment between crosses will give more sides, as shown in the schema. Let us consider as positive the polygon whose sides begin in an up position and finish down when going in the clockwise direction of gyration (_`), and negative the opposite, as can be seen in the schema.
Since only two frames intersect at a time (R10), their crossing create four angles, two contiguous polygons sharing only one segment of frame, and four polygons sharing a node. Now, it is easy to see that, if we select a positive polygon, those contiguous to it will be negative, and the other one, opposed by the angle, positive. That gives give us a rule to intersecting: we choose one polygon as positive and all the others will take their respective sign; the frames will be then interwoven accordingly. See nudos on this subject.
MODELLING a Rige
To understand and code a Rige implies finding out the following:
1‒The lattice to which it belongs.
2‒The particular use of this lattice by this particular Rige, that is, what segments are included in it.
3‒This use can be simplified when, as usual, a smaller part of the form can be found, which engenders the rest by simple geometric operations, as symmetries (axial, central) -the GE-, and/or displacements -the TE-.
Those operations are not always simple to find out, especially in large orders, such as 24, 36, and so on; in these cases the angles are not easily discriminated (see Lattice Orders, above).
In any case a segment is defined by the straight line to which it belongs, and by its two extremes, determined respectively by two other straights. Thus a segment is defined by three straights. A straight in our model is defined by two elements: the angle of the main direction of the straight, and its distance to the centre. Both parameters are determined by two integer indexes, that of the angle, between 0 and N-1 (order), and that of the distance, an integer between 0 (straight passing on the centre) and D, the maximum number of distances which the form uses which is always limited and finite.
A simpler method for defining segments could be found: the Cartesian coordinates of their extremes. However, this would not allow either the perception of symmetries, or the use of the inner limitations of the lines position, which simplifies greatly the selection for human users: they will introduce the straight index of distance (1,2,3...) and the index of basic angles (1,2,3,..). It is much simpler to see two straight segments in cross, gyrated 30 degrees, than list their end coordinates (see Computer Implementation, in Apendix.2).
The symmetries of the system allow an easy definition, but by limiting the possibilities, as in any form of ar
By Metabolê, a term taken from the old Greek theory of music, we understand a local change in the lattice of a Rige. That directly violates our R2 rule; however the rule holds, but only in an specific area, while another lattice becomes valid in the new one. In fact, a unique lattice can comprehend both local lattices, and no concept of metabolê should be required: only the specific use of this universal lattice by a Rige would then focus on some straights or others. But there are some justifications for that new concept: first, perception selects easily two areas in an actual metabolê; second, the combined lattice would became very complex, and underused.
|
Fig.3. Rige "Azulejos". |
Several types of metabolai (plural of metabolê) can be considered: the first, the simplest one, consists of only a turn of the first lattice; it is the same, but with a different reference or direction 0. An example can be two concentric 8-lattices with a circular shift of half basic angle. See in Fig.3 this metabolê and its beautiful effect, in a Rige that can be found in the Alhambra, Granada (Spain). The lattice could be a unique 16-one, but also two concentric 8's. The choice would depend on the simplicity of computer implementation (see below).
A second type of metabolê, also simple, can appear: a change which keeps reference angles but jumps to a multiple or submultiple order. In those cases, both lattices share the main directions, but one of them introduces another set of main directions, in a symmetrical way, as the new directions will be inserted between the old ones. For example we can change from 8 to 16, or from 24 to 12. As before, a global or universal lattice can include both if desired.
A somewhat more complex metabolê, similar to the former, is a change to an order which share some divisor, their integers have a maximum common divisor, as in the cases 8 to 12 (m.c.d.=4) or 9 to 24 (m.c.d.=3). In this case, a global lattice can include both of them, too.
The most complex metabolê consists of a change between two prime orders, like 12-13 (never found by the author!). However, more simple changes between numbers which share only the factor '2' are used sometimes, as 10-12, in a wood door in the National Museum in Baghdad. Another rare example can be found in the Alcazaba museum of Malaga, where a Nazari relief (about XV century) shows a rare metabolê from a central part on 8-lattice, and 4 parts on a 7-lattice. This example is, perhaps, a "tour de force" from an Art in decline. But an even more complex example found by the author is the one in Konya, Turkey, which uses three different lattices, 16, 12 and 10, that coexist harmoniously here. See in Ap.1, the graphic analysis of both forms (fig.14-16).
The metabolê has an exemplary value for us: it changes references, and/or circle divisions, in the same way that musical metabolê changes the reference, in tonal or modal tonic, or the division of octave or tetrachord: the genus Rast on note rast can change to Rast on naua ‒reference change‒ or to Nahauand on note rast ‒division change‒ (see below, musical Relationship, and [Barker,1989. Sánchez,1993-a]), The Rige metabolê, like its musical counterpart, allows keeping simplicity while introducing variations: the psycho-aesthetic effect is to allow easy recognition and appreciation, which becomes denser after some study, as with some masterpieces.
RHYTHM
|
Fig.4. Olive tree plantation showing repetition gap according to complex tangent. |
The concept of rhythm involves repetition of a pattern at equal (or almost equal) intervals, whether in a visual or in a sound dimension. The sight of any Rige unavoidably suggests of rhythm: following any (straight) direction passing over a centre (a main direction) we see particular patterns that trail or circulate with regularity, forever until limits of the form are reached.
In our model this concept is basic, since we define the EE and TE as patterns that repeat themselves in several stages (a first one, circular, for EE, and two straight after, for TE) at equal intervals (angles or distances). Thus, this leads us to three primary rhythms that are almost always found, one circular, two straight.
|
Fig.5. Rige "Alcazar", proposing infinite patterns. |
But these constructive repetitions are by no means the only ones which can be found. As in regular tree plantations ( I remember olive trees in Andalusian Spain) any direction will find a regular line of trees, the more numerically complex the slope or tangent, the wider the gap. In the same way, different and longer patterns appear when more complex slopes are chosen. Look at "Alcazar" Rige. nn and find more complex pattern than the obvious ones. In the same way as in musical and poetical rhythm, a conventional beginning must be establish, so as to select the material that fills the periodically repeated space perceived as a pattern. In visual matters this beginning is related to the relative position between observer and figure; usually horizontal or vertical references are taken ( that is directions parallel to the eye line or perpendicular to it. This is the reason for which the aspect of any Rige changes so much when it is turned: different references are taken and therefore different patterns. Again test this effect with the "Alcazar" Rige. If still a new beginning brings out new patterns as well.
|
Fig.6. Some pattern choices in "Alcazar", becaming rhythmical by joining with equals at equal intervals (any direction). |
In fact, each time any observer beholds a Rige, even the same, he or she chooses another path, and find a new pattern that magically appears. First the smaller ones, usually in neighbour TE. Afterwards TE are transcended, and wider forms can be seen when the Rige size is great enough. These effects gives the Rige art a complexity, interest and richness that a hurried look cannot fathom. And so the Rige decoration acquires an artistic touch, which part it from geometric filling of surfaces
musical RELATIONSHIP
This kind of form, the Rige, suggests intense remembering of Music [Burckhardt, 1976], an Art being considered as the paradigm of Harmony and Rhythm; that is, with a balanced relationship between its units (notes and strokes); temporal, pitch and sonance vicinity; grouping of them in superior units (motifs), and contrast and similitude between units in every level [Sánchez,1993-a]. Indeed, many formal similarities can be established between both arts; and this research is a beautiful task. Let us highlight one of them:
If the EE seen in Fig.3. are considered as units, the more symmetrical, it will be the more attractive for the eye (the visual perceiver), and therefore there will be a rest before another eye movement; they strongly attract the attention and become centres. In that sense, this is akin to the momentary rest that occurs in music at some notes: the more consonant the note, and higher in the mode hierarchy [Sánchez,1993-a], the higher the rest, and, now in Rige art, the more symmetric, the more restful. In this respect, the maximum symmetry is that of the lattice order, N, which present polygons or stars of N points. They would represent the most important centres, the centres of the Rige, as the modal tonic and its octaves represent the reference note in modal music.
Therefore, as in music, melody (and auditive perception) moves between notes of the scale with temporary rest at important notes (let them be called king, wizir, courtiers, enemies, as in Indian terminology), in Rige art too, the eye (and visual perception) will move between centres through less symmetric (consonant) EE, in an arsis-thesis contrast, necessary for every kind of Art and even for every grateful impression.
Many more similarities are to be found, as the metabolê formerly reviewed. A following paper will discuss them further in detail, and show those which we found ourselves, probably not all what could be found. But now to go further in this direction would be to go beyond the scope of this exposition: let us thus finish the subject here. By way of conclusion: A Rige is a non-limited Form, only the observer limits its possibilities; since they are many observers with different levels of intuition and artistic perspicacity, there will be many readings of the same Rige, as in any other form of Art.
COLOURS
|
Fig.7. “Mevlüt”,
a mosque door. |
The colours used in the actual Rige usually emphasíze both the continuity of the frames, the contrast with the inner figures, and the symmetries. Contiguous colours are thus different and contrastive as a general rule. From a minimum of two colours, for frames and figures - figures and background-, we can pass to a great number; but the artistic use of this richness is difficult, and a banal colouring can be the result, especially in computer graphics.
An important quality of the colour is the Texture, which improves the variation without breaking the basic colours. This texture, present in every natural material, must be simulated in computer work; PUERTRA has implemented some possibilities in this direction, as the figures show.
SYMBOLOGY
The Islamic craftsman gives a deeper meaning to his designs by means of a symbolic message, usually religious and numerical. In this way, his work and its product acquire greater importance. This meaning must also be understood by the observer, in order to grasp the full significance of the piece of art.
|
Fig.8. "Occidental"/Western. Design. |
For instance, the Rige shown in fig. 7 is used by a Turkish kündekare (Mevlüt Chilar, Konya, master carpenter) in most of his mosque doors. To him, this design is full of meaning because the number of its pieces is 99, the number of Allah's names. Another case, an older one: during the roof restoration of the Salón de Comares, in Alhambra (Granada), a piece was noted to be better finished than the others. Once it was detached, an inscription appeared on its back, with an explanation for the meanings of the colours and for the number of main designs that form the ensemble [Cabanelas,1988].
All this shows that aesthetics alone does not explain completely this and other kinds of Islamic Art. See also references [Ardalan and Bakhtiar, 1979, Abou-esh, 1970, Burckhardt, 1976] on the symbology of zakhrafa.
AN EXAMPLE DESIGN
By forcing a little the formal rules stated above we arrive to a somewhat different type of Rige, slightly changed. In Fig. 8 we see an example developed with PUERTRA, which shows a different flavour, not longer oriental-Islamic, but what could be called Western (we call it Occidental). In it a rule -R10: frames do not bend at crossing points- has been not followed. The example shows the possibilities of the program, together with the apparent goodness of the Rige model. In Appendix 1 some more examples are included, also designed and printed by PUERTRA, unless being actual designs.
REFERENCES
ARDALAN,N. & BAKHTIAR,L.The sense of Unity. Chicago Press. Chicago, London, 1973,1979.
AUDSLEY,W & G. Designs and Patterns from Historic Ornament. Dover. N.York.1968.
ABOU-ESH, I.M. Design Concepts of Islamic Arquitecture. Dar Al-Arabiyah. Beirut, 1970.
BARKER,A.(ed):Greek musical Writings,book II:Harmony&Acoustic Theory. Univ. Pres. Cambridge. 1989
BOURGOIN, J. Arabic Geometrical Pattern & Design. Dover, N.York. 1973.
BOURGOIN, J. Islamic Patterns. Dover, N.York. 1977.
BURCKHARDT,T. Moorish Culture in Spain. Allen & Unwi. Lond,1972.
BURCKHARDT,T. Art of Islam. Language and Meaning. World of Islam Festival. London, 1976.
CABANELAS,D. "El Techo del Salón de Comares en la Alhambra". Patronato Alhambra. Granada, 1988.
COXETER,H.S.M. Regular Polytopes. Dover, N.York.1973.
CRITCHLOW,K. Islamic Patterns. Thames & Hudson, London, 1992.
GHICA,M.C. Estética de las Proporciones en la Naturaleza y en las Artes. Poseidón. Barcelona, 1977.
GRABAR, O. Los fundamentos del arte islámico. Cátedra, Madrid, 1984.
JAWAD al-JANAB,T. Studies in Medieval Architecture. Ministry of Culture & Information Baghdad, 1982.
MARTÍNEZ, B. "Carpintería Mudéjar Toledana". Cuadernos Alhambra,12. 1976.
NUERE, E. La Carpintería de Armar Española. Ministerio.Cultura. Madrid, 1989.
NASR,S.H. Islamic Art and Speirituality. Golgonooza. Ipswich, 1987.
ÖGEL,S. Anadolu Selçuklulari'nin TaÕ Tezyinati. Türk Tarih Korumu Basímevi, Ankara,1987.
PAVÓN MALDONADO,B. El Arte Hispano-Mulsulmán en su Decoración Geométrica. Min. Cultura y Agenc. Española. Cooperación Internacional. Madrid, 1981, 1990.
PRIETO y VIVES, A. El Arte de la Lacería. Coleg.Ingen. Caminos Canales Puertos. Madrid, 1977.
RADEMACHER & TOEPLITZ. Números y Figuras. Alianza, Madrid,1970.
SÁNCHEZ, A. Trigonometría Rectilínea y Esférica. Lib.Romo. Madrid, 1944.
SÁNCHEZ,F.J. "ESCALA, Automatic Measurement of Oriental Scales". Proc. ICEMCO. Univ. Cambridge. London, 1993-a.
SÁNCHEZ,F.J. "PUERTRA, a Model of Islamic Rectilinear Interlaced Lattices". Proc. ICEMCO. Univ. Cambridge. London, 1993-b.
SPELTZ, A. The Styles of Ornament. Dover, N.York. 1959.
VARDERBROECK,A. Philosophical geometry. Inner Traditions Inter. Rochester, 1972.
WILSON, E. Islamic Designs. Dover. N.York. 1988.
Vuelta al Principio Última
actualización:
viernes, 18 de septiembre de 2015 Visitantes: