Catálogo de redes de 12 (perteneciente a Decoración Geométrica Islámica)
A partir del estudio en Diseño de redes de 12, y siguiendo el modelo del Catalogo de redes 8 catalogamos entre las infinitas posibles las más sencillas en forma escalonada y creciente desde la mínima. Recordamos que la codificación de cada una consiste como antes en:
1. Orden de las red.
2. Semisecuencias de las distancias entre paralelas de las series oblicua (X) y recta (H), a partir del eje de simetría principal del bloque de traslaciones, con su número al final. Entre paréntesis cuadrados. Los paréntesis redondos (estos sí añadidos manualmente) representan posibilidad de permutación libre (cumpliendo eso sí con la condición de capicúa de la semisecuencia oblicua. Aparecen los siguientes símbolos de esas distancias::
a; mayor c; menor á; mitad de la mayor ç; mitad de la menor â, diferencia entre mayor y menor o, nula.3. Suma de ellas en unidades a y c, las dos distancias principales cuya relación depende del orden. 4. Relación o cociente a/c.
Recordamos que nos limitamos a redes con sólo dos distancias entre paralelas (ello excluye en realidad a la distancia â, que sería una tercera. .Nótese también que las medias distancias devienen una entera al repetir el bloque por simetría.
Pero primeramente veamos esta serie de redes generadas cada una de la anterior por adición de nuevas distancias, siempre cumpliendo las condiciones que vimos en Diseño de redes de 12, que no fueron concluyentes, de modo que iremos paso a paso a ver si las descubrimos empíricamente.
1. Proyección de X en H: : X[ 2ba+2gc ] ' = H[ ga+3bc ]. (1) 2. X capicúa: X[ i ] = X[ loX - i ]. (2)
que podemos poner en palabras, mucho más farragosamente) de esta maneta:
1. El número de interdistancias (entre dos rectas paralelas contiguas) de valor 'a' (el mayor de los dos) en la semisecuencia oblícua ha de ser par, es decir múltiplo de dos, producto de 2 por un entero b (b=0,1,2...). El número de interdistancias c (la menor) en la semisecuencia horizontal ha de ser el triple de ese numero b.
2. El número de interdistancias c en la semisecuencia oblícua ha también par, múltiplo de 2 por g (g=0,1,2...). El número de interdistancias a en la semisecuencia horizontal es ese numero g.
3. La semisecuencia oblicua es capicúa (par o impar).
Veamos las posibilidades que nos ofrecen las dos primeras leyes.
| b -g | 0 | 1 | 2 | 3 | 4 |
| 0 | ‒ | X[2c ] H[a] | X[4c ] H[2a] | X[6c ] H[3a] | X[6c ] H[3a] |
| 1 | X[2a ] H[3c] | X[2a2c ] H[a3c] | X[2a4c ] H[2a3c] | X[2a6c ] H[3a3c] | |
| 2 | X[4a ] H[6c] | X[4a2c ] H[a6c] | X[4a4c ] H[2a6c] | ||
| 2 | X[6a ] H[9c] | ||||
| 3 | X[8a ] H[12c] | ||||
| 4 | |||||
| 5 |
Estas dos leyes nos proponen un modo de generación de nuevas redes a partir de las anteriores mediante la adición en de un par 'a' o mediante la adición de un par de 'c'. Se nos presenta un triángulo parecido al de Tartaglia al disponer las secuencias oblicuas en orden creciente:
2a2c a3c 4a2c 2a4c a6c 2a4c 6a2c 4a4c 2a6c a9c 2a6c 3a6c 8a2c 6a4c 4a6c 2a8c a 12c 2a9c 4a6c 4a3c 10a2c 8a4c 6a6c 4a8c 2a10c a5c 2a4c 3a9c 4a8c 5a10c ... ... ...Ahora bien, los datos obtenidos son sólo la suma de interdistancias totales de cada semisecuencia. Pero ahora hay que disponerlas en orden. Y además hay que decidir si en el principio y final de esas semisecuencias, es decir, junto a los ejes de simetría del elemento generador de bloque, el triángulo que genera toda la red., se colocan medias calles 'a ' o 'c'. Y si esa elección es común a ambas semisecuencias X y H o cada una puede elegir con independencia. Ahora deberá cymplirse además de las dos primera, la tercera ley que requiere carácter capicúa en X.
Con todas estas posibilidades, la familia de redes se hace complicada y extensa.. Por ejemplo, X[2a2c] (simétrica) puede realizarse como X [//çacaç] o como X [//ácacá], según elijamos semicalles 'a (a/2) o ç (c/2). A su vez H[a3c] (libre en su orden) puede realizarse como H [//ácccá] y como las tres combinaciones de H [//ç(cca)ç] , permutando los elementos dentro del paréntesis (cca, cac, acc). La combinación libre de X y H nos proporciona ya 6 posibilidades. Y esto solo en esta sencilla combinación de a y c. Imaginemos las posibilidades una mayor.. Ya para X[6a6c] encontramos X[[//á(cccaa)a(aaccc)aá] y todas las posibilidades permutando los elementos dentro de ambos paréntesis de manera simétrica (capicúa) lo que implica ya 20 posibilidades (al la secuencia 'ccc' le colocamos 'a' en cada posible lugar, lo que nos da 4 posibilidades. A cada uno de esas cuatro le colocamos el segundo 'a' en todas las posiciones, lo que nos da 5 por cada una de las 4 anteriores: 4.5=20) . Y las correspondientes de la semisecuencia H serán ya más de cien. En efecto, H[3a9c] puede realizarse como H [//á(aa ccc ccc ccc)á] (separo bloques por claridad) lo que nos proporciona, con igual razonamiento que antes, 10*11 = 110 posibilidades sólo para el caso de semicalles +a (a/2) (pero cada grupo de aa que aparece se cuenta dos veces, luego es 110/2 =55 (son permutaciones con repetición, N=(11!/2! 9!)=11*10*.../2* 9*8*... =55. ). Para semicalles ç (c/2) tenemos H[//ç(aaa ccc ccc cc)ç] lo que supone N=(11!/3! 8!)=11.10.9.8.7.../3.2.8.7.6.... =11.10.9/3.2= 165).
Luego, combinando X y H libremente obtenemos ya un gran número: 20 * (55 + 165) = 4400 posibilidades de red periódica.
Presentemos pues algunos de los ejemplo más sencillos, dejando al lector interesado que construya su red.
Veamos ahora el catálogo anunciado, desde la mínima, las mínimas en realidad, porque podemos elegir semicalles de anchura 'c' o semicalles de anchura 'a'.
La codificación la ofrece el programa PUERTRA, no está retocada ni editada, y corresponde a la figura que aparece encima.
Las ordenamos por tamaño total, es decir, por el tamaño de la suma ba+2gc]. Colocamos juntas las opciones obtenidas por permutación de los elementos en los paréntesis. Representamos a igual escala, manteniendo los valores de las distancias a y c en el dibujo para que se aprecie el crecimiento de tamaño junto a la de complicación.
| Casos mínimos de semicalles diferentes en X y H. Cruce de red en extremos del EGR | |
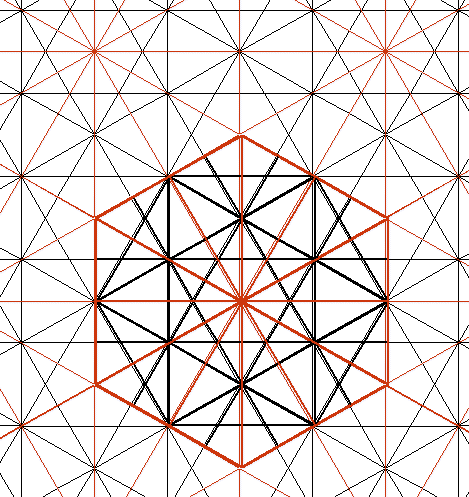 |
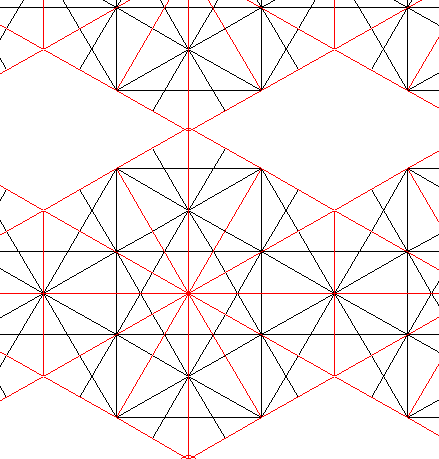 |
| Red 12. X [//çcç: 3] H [//áá: 2]. sX[ 0a+ 2c ] sH[ 1a+ 0c ]. Dispos: dx=1. dy=0.87 dz=0.5. Disposición contrapeada o al tresbolillo. | Red 12. X [//çcç: 3] H [//áá: 2]. sX[ 0a+ 2c ] sH[ 1a+ 0c ]. Dispos: dx=1. dy=1. dz=0. Disposición paralela |
| Caso mínimo siguiente de semicalles diferentes en X y H. Cruce de red en extremos del EGR | |
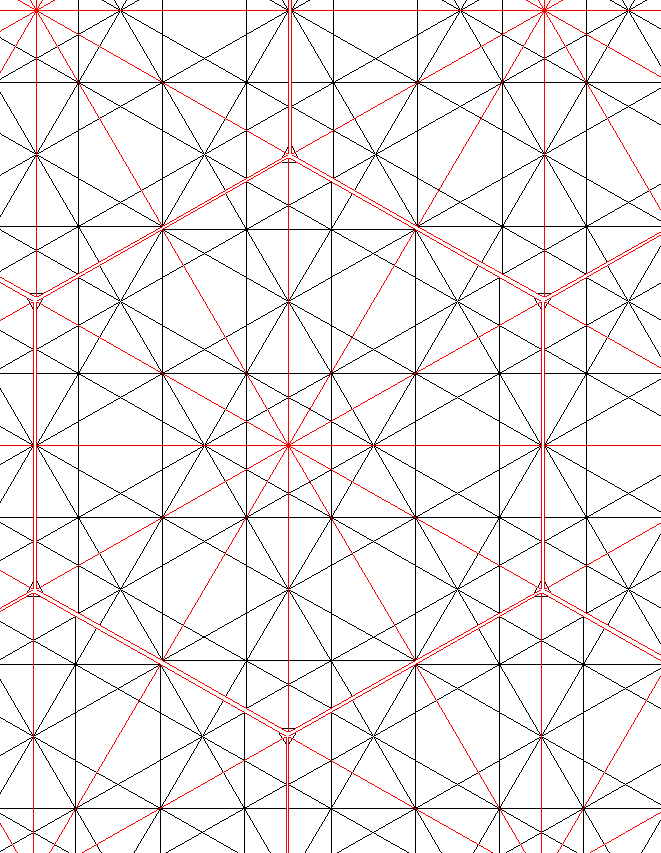 |
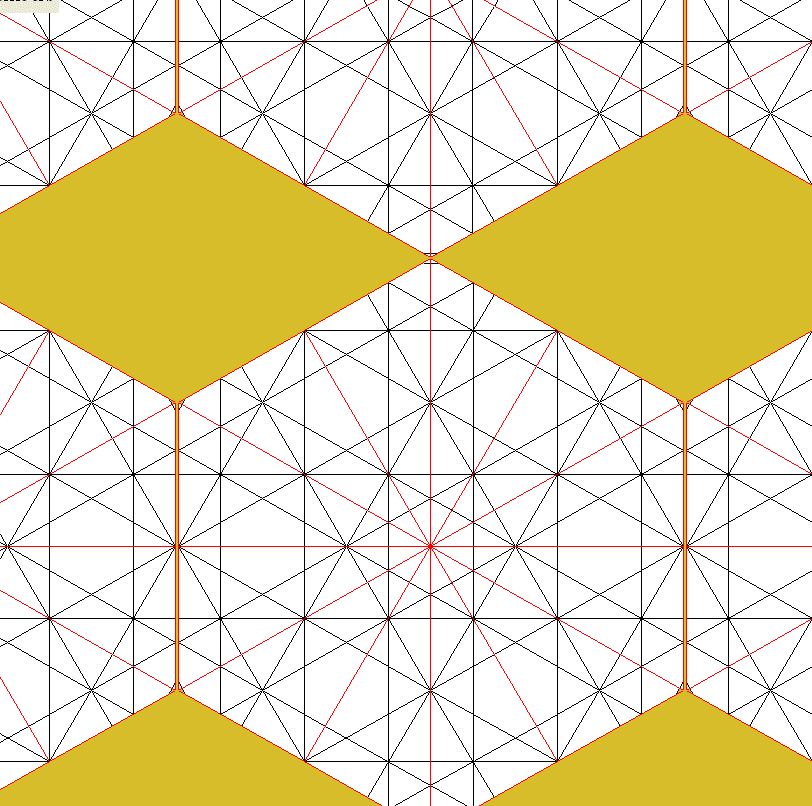 |
| Red 12. X [//áaá: 3] H [//çccç: 4]. sX[ 2a+ 0c ] sH[ 0a+ 3c ]. Dispos: dx=1. dy=0.87 dz=0.5 Disposición contrapeada o al tresbolillo. | Red 12. X [//áaá: 3] H [//çccç: 4]. sX[ 2a+ 0c ] sH[ 0a+ 3c ]. Dispos: dx=1.01 dy=1.16 dz=0. Disposición paralela |
El caso mínimo sin cruces y satisfactorio desde cualquier punto de vista es:
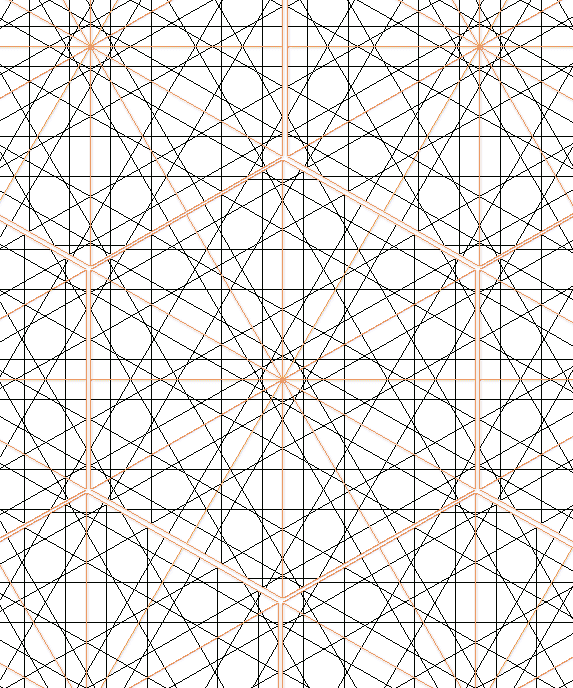 |
| Red 12. X [//çacaç: 5] H [//çcacç: 5]. sX[ 2a+ 2c ] sH[ 1a+ 3c ]. Dispos: dx=1. dy=0.87 dz=0.5 |
Y así sucesivamente. Vea más casos en
Diseño empírico de redes de 12. De allí tomamos el caso complicado de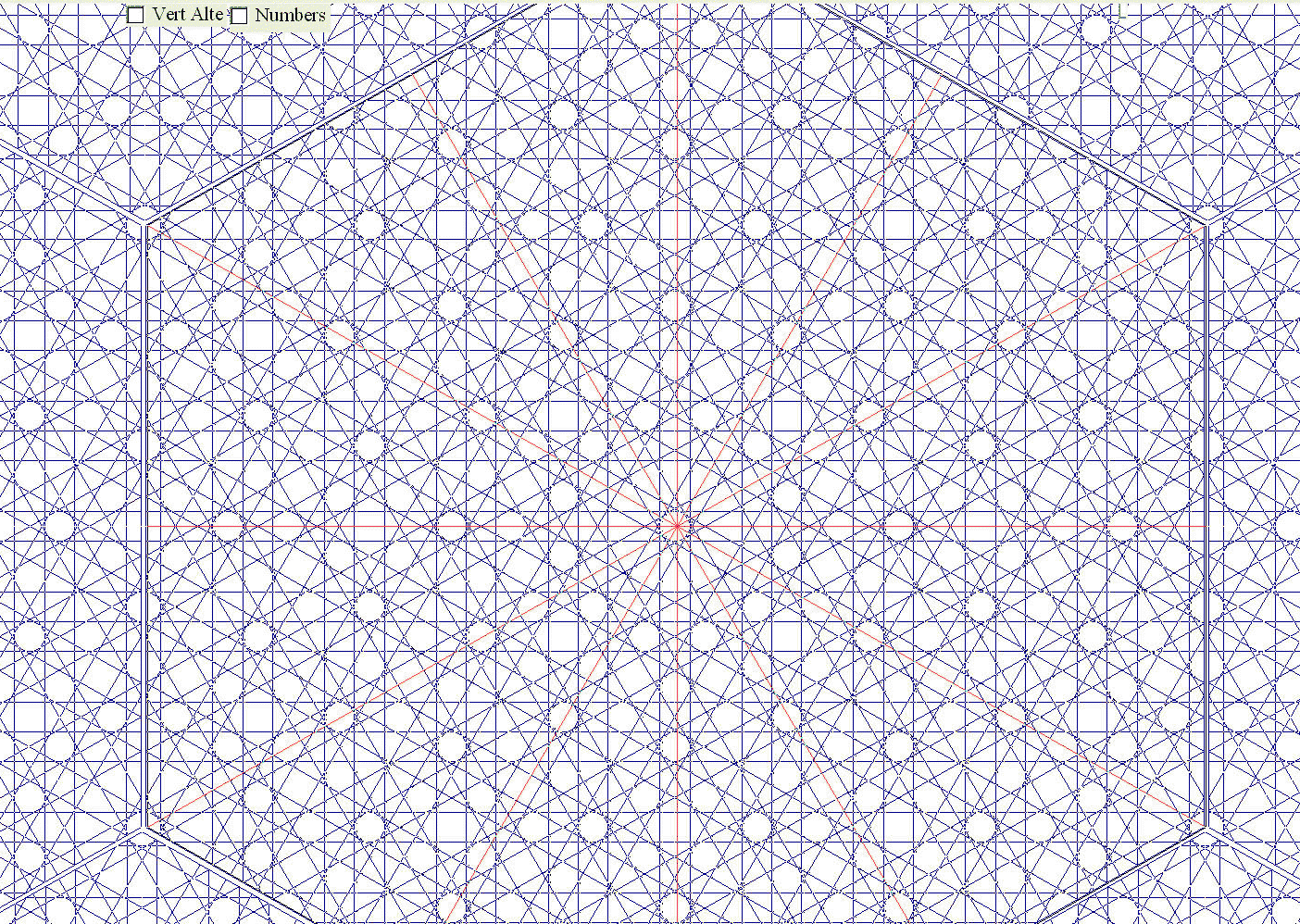 |
| Red 12 Oblicuo: X [//çaccaccacaccaccaç: 17] Recto: H [//çaccaccaccaccaç: 15] sH[ 5a+ 9c ] sX[ 6a+ 10c ] Dispos: dx=1. dy=0.87 dz=0.5. Semicalles ç. Disposición al tresbolillo. |
Nótese como siempre el 'reflejo' aparente de todas las rectas de la red en los límites y ejes de simetría, en rojo, que aseguran la prolongación correcta de la red interior en el exterior, hasta el infinito.
Vuelta al Principio Última
actualización:
viernes, 18 de septiembre de 2015 Visitantes: