Diseño empírico de redes de 12 (perteneciente a Decoración Geométrica Islámica)
A partir del estudio en Diseño de redes de 12, intentamos hallar las leyes de manera empírica (probando):.
Red 12 Recto: H [//: 7] Oblicuo: X [//çcaacç: 6] sH[ 2a+ 4c ] sX[ 2a+ 3c ]
Red 12 Recto: H [//çacccaç: 7] Oblicuo: X [//çcaacç: 6] sH[ 2a+ 4c ] sX[ 2a+ 3c ]
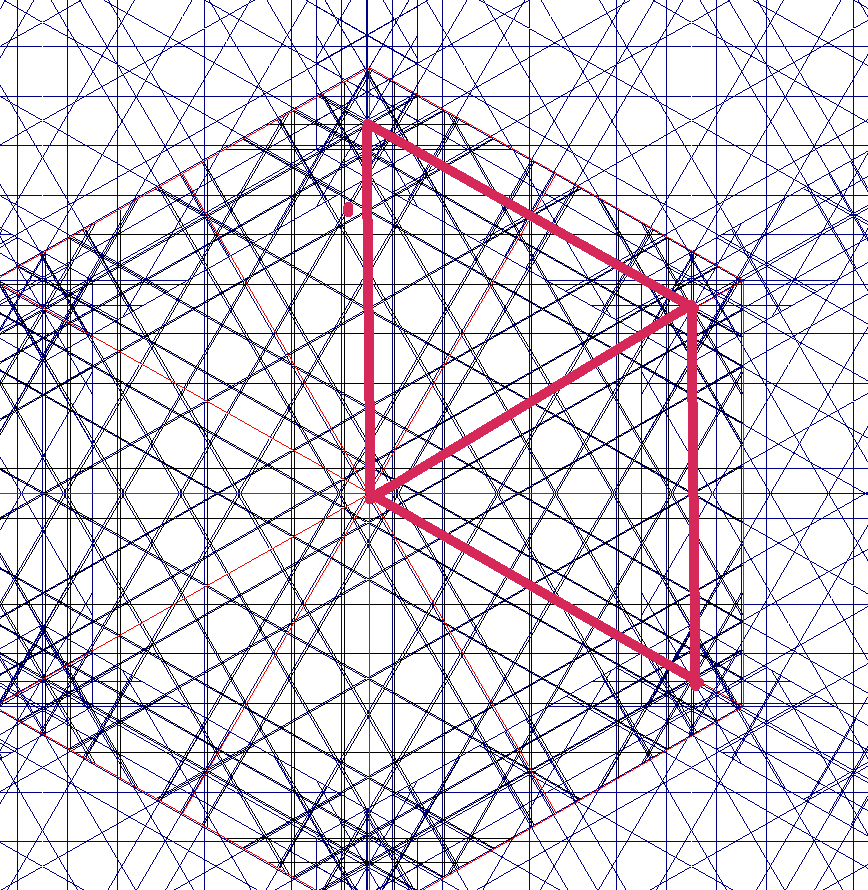
Red 12 Recto: H [//çacccaç: 7] Oblicuo: X [//çcaacç: 6] sH[ 2a+ 4c ] sX[ 2a+ 3c ] Número de 'c' en oblicuo ha de ser par Número de 'a' en oblicuo ha de ser tres medios de número de 'c' en recto Número de 'c' en oblicuo ha de ser doble que número de 'a' en recto Dispos: dx=1. dy=1. dz=0.
Red 12 Recto: H [//çacccaç: 7] Oblicuo: X [//çcaacç: 6] sH[ 2a+ 4c ] sX[ 2a+ 3c ] Número de 'c' en oblicuo ha de ser par Número de 'a' en oblicuo ha de ser tres medios de número de 'c' en recto Número de 'c' en oblicuo ha de ser doble que número de 'a' en recto Dispos: dx=1. dy=1. dz=0.
oblicuo ha de ser par Número de 'a' en oblicuo ha de ser tres medios de número de 'c' en recto Número de 'c' en oblicuo ha de ser doble que número de 'a' en recto Dispos: dx=1. dy=1. dz=0.

 |
De manera empírica obtenemos la línea
adicional 6ª mediante la diferencia a-c = â en la oblicua. Esto parece
sugerirnos un nuevo eje de simetría en medio de esa distancia, que
podemos repetir en la mitad interna, aunque nos es necesario.
Red 12 Oblicuo: X [//çcâcccâcç: 9] Recto: H [//çaccaç: 6] sH[ 2a+ 3c ] sX[ 2a+ 4c ] Dispos: dx=1. dy=0.87 dz=0.5 sigue funcionando. El problema es que ahora tenemos tres distancias y no sólo dos. repetimos en H el proceso en H y obtenemos la solución siguiente |
| Red 12 Oblicuo: X [//çcaccâcç: 8] Recto: H [//çaccaç: 6] sH[ 2a+ 3c ] sX[ 2a+ 4c ] Semisecuencua oblicua no es capicúa. Dispos: dx=1. dy=0.87 dz=0.5 |
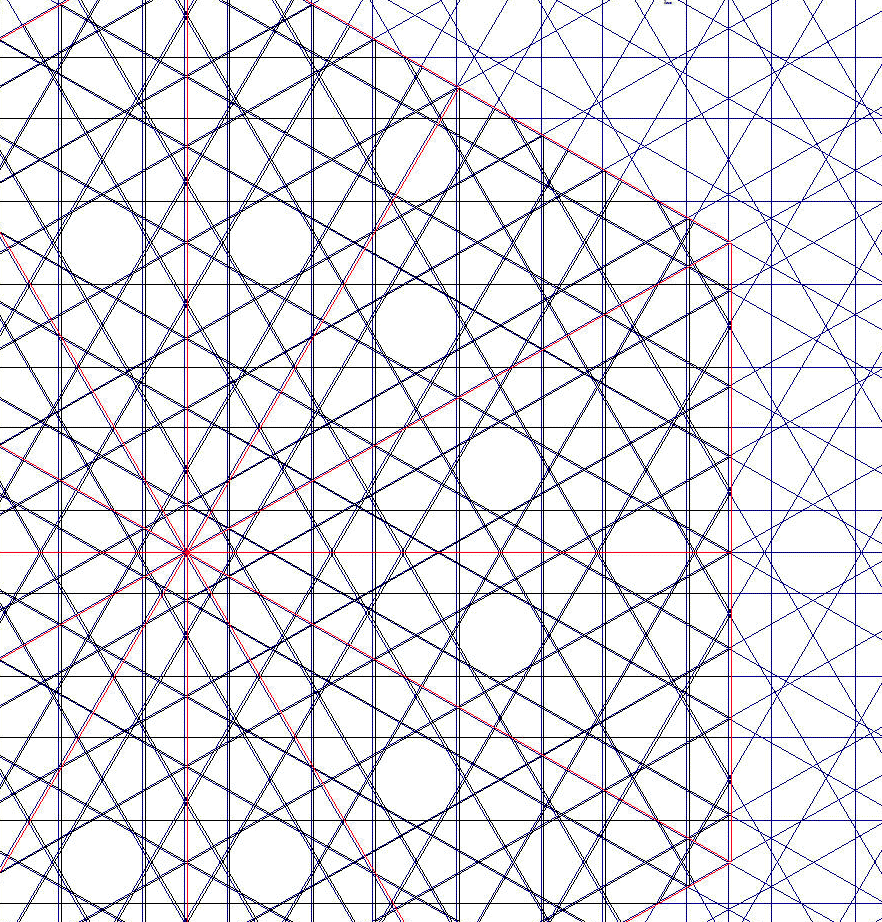 |
Ambas semisecuencias doblemente capicúas,
o capicúa doble (como dos periodos de función seno Intentamos lo mismo pero con nue3stras dos deistancias interlínea originales, a y c: |
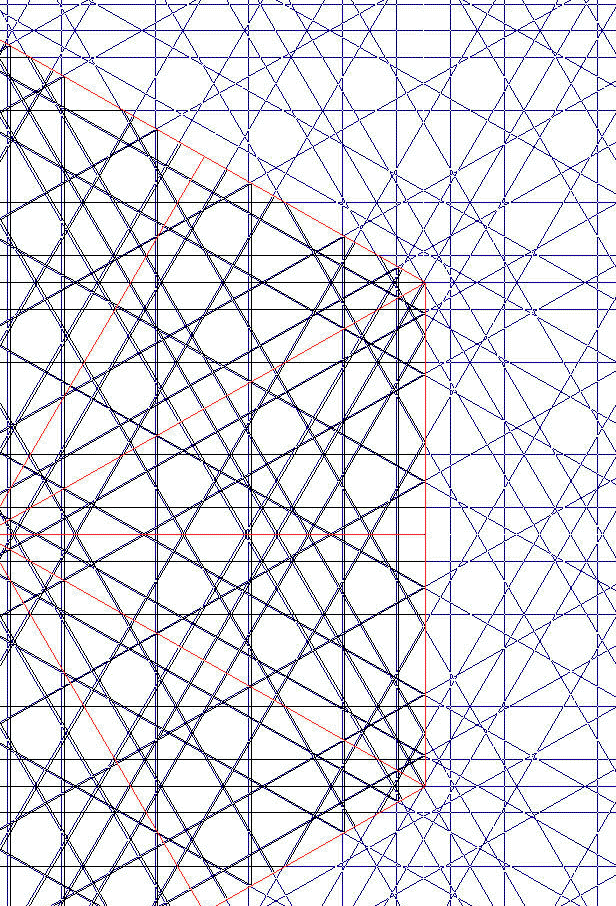
| RRed 12 Oblicuo: X [//çcâcccâcç: 9] Recto: H [//çcâccâcç: 8] sH[ 2a+ 3c ] sX[ 2a+ 4c ] Dispos: dx=1. dy=0.87 dz=0.5 |
 |
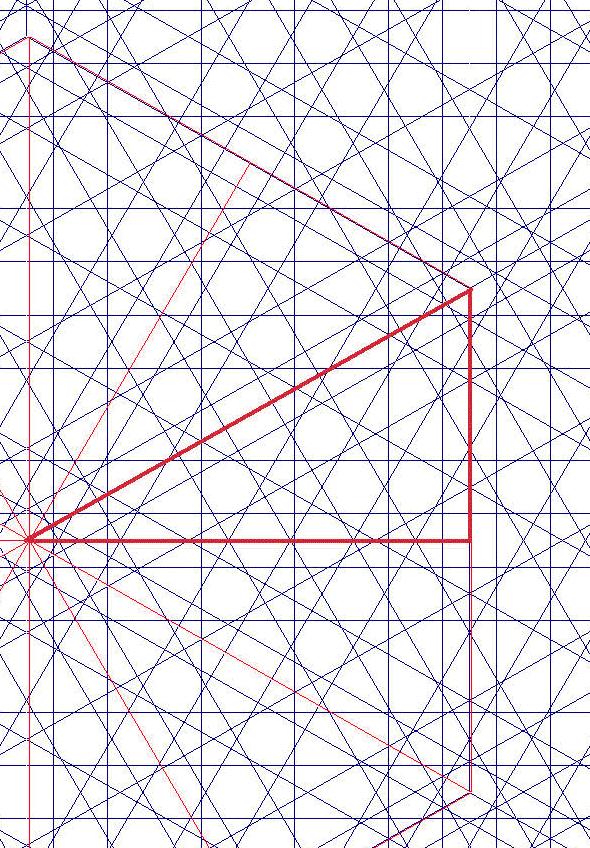 |
| Red 12 Oblicuo: X [//çcacççcacç: 10] Recto: H [//çcaaacç: 7] sH[ 3a+ 3c ] sX[ 2a+ 6c ] Dispos: dx=1. dy=0.87 dz=0.5. Elimino línea central de çç en oblicua: | Red 12 Oblicuo: X [//çcacccacç: 9] Recto: H [//çcaaacç: 7] sH[ 3a+ 3c ] sX[ 2a+ 6c ] Dispos: dx=1. dy=0.87 dz=0.5 |
Comprobamos que la semisecuencia oblicua afecta los rayos reflejados de 60º mientras que la recta H, afecta los de 30º
Reglas provisionales al parecer suficientes para conseguir
Reglas para redes periódicas de 12 disponiendo los BR en panal de abeja:
1. Coeficientes de las combinaciones lineales de a y c en oblicuo X y recto H cumplen:
X[ 2ba+2gc ] ' = H[ ga+3bc ]. (1)
2. X es capicúa doble y capicúa: *** retocar ley
X[ i ] = X[ loX/2 - i ]. X[ i ] = X[ loX - i ]. (2)
2. H es capicúa:**
H[ i ] = H[ loX - i ]. (3)
Lo comprobamos en una complicada:
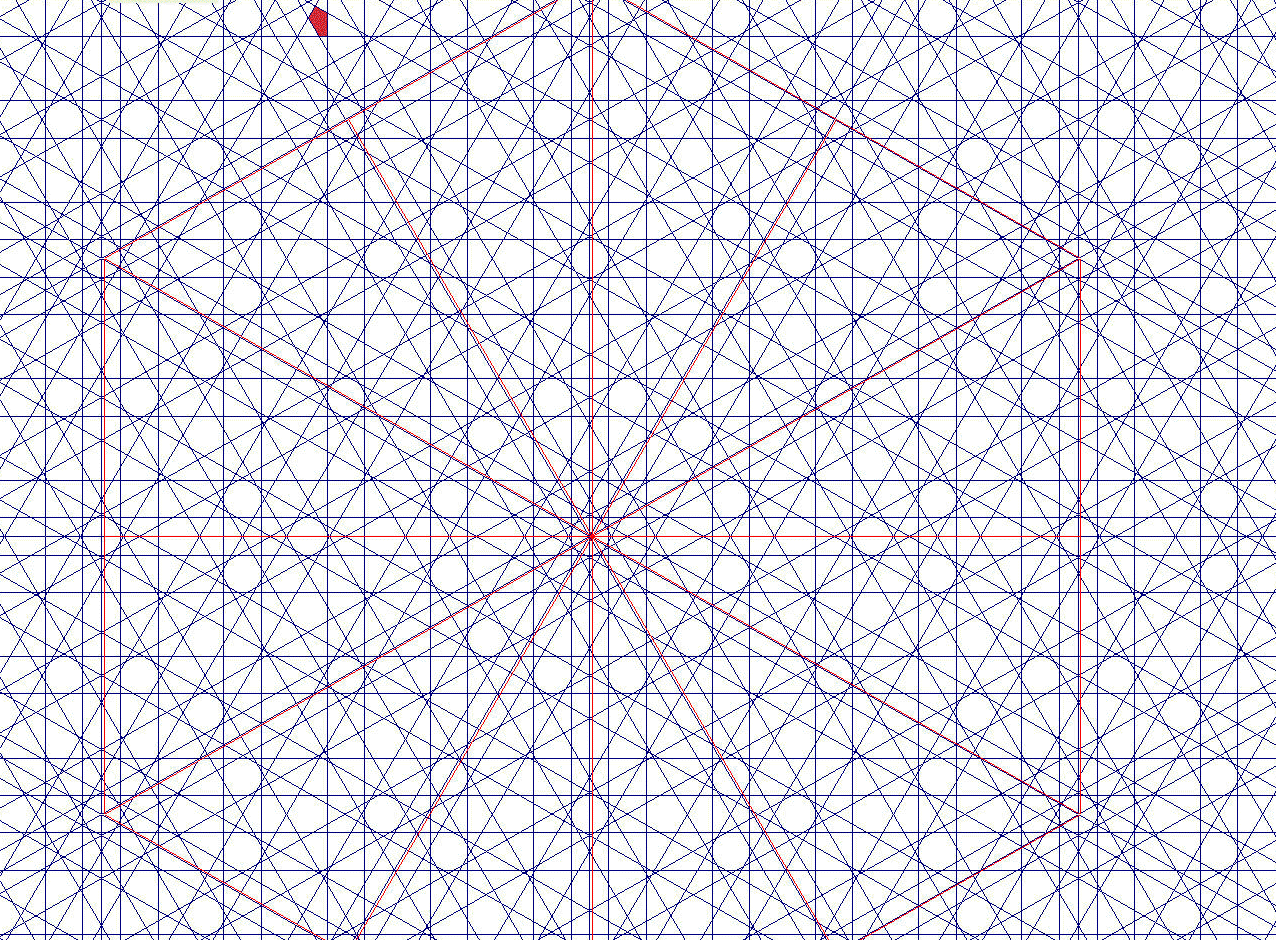 |
| Red 12 Oblicuo: X [//çcacacccacacç: 13] Recto: H [//çcacacacacç: 11] sH[ 4a+ 6c ] sX[ 4a+ 8c ] Dispos: dx=1. dy=0.87 dz=0.5 |
Más aún, llegamos, esta vez correctamente a sX[ 6a+ 10c ] sH[ 5a+ 9c ] : nuestras leyes empíricas funcionan.
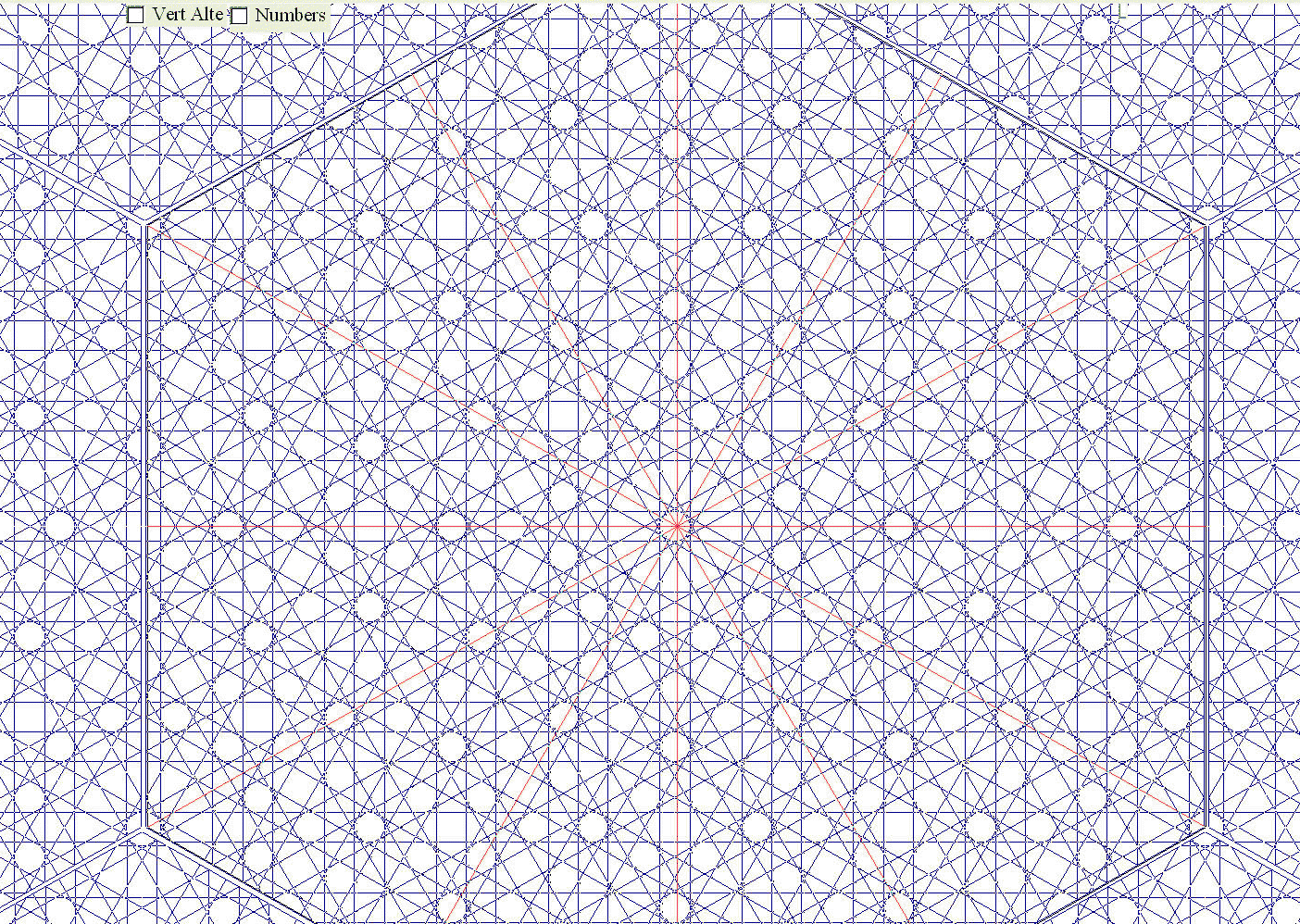 |
| Red 12 Oblicuo: X [//çaccaccacaccaccaç: 17] Recto: H [//çaccaccaccaccaç: 15] sH[ 5a+ 9c ] sX[ 6a+ 10c ] Dispos: dx=1. dy=0.87 dz=0.5 |
que podemos adosar diferentemente, en paralelo, como la red de 8. Rellenamos a mano el hueco en el primer caso este caso:
 |
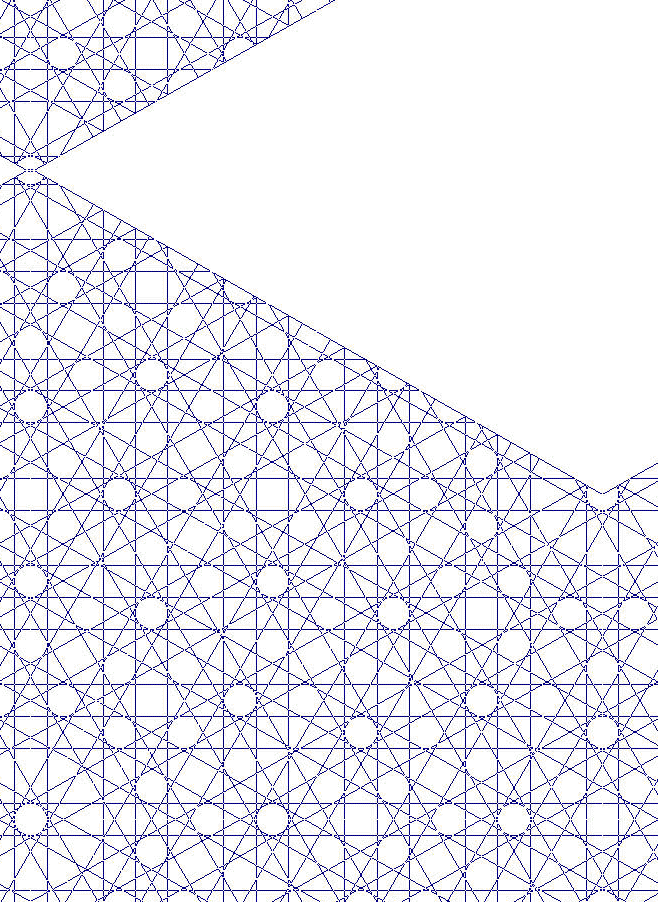 |
| Red 12 Oblicuo: X [//çccacccccaccç: 13] Recto: H [//çacaaacaç: 9] sH[ 5a+ 3c ] sX[ 2a+ 10c ] Dispos: dx=1. dy=1. dz=0. | Red 12 Oblicuo: X [//çaccaccacaccaccaç: 17] Recto: H [//çaccaccaccaccaç: 15] sH[ 5a+ 9c ] sX[ 6a+ 10c ] Dispos: dx=1. dy=1. dz=0. |