Un modelo de arco más detallado (forma parte de Arqueria)
Este modelo debe tener en cuenta algunas condiciones no consideradas antes en Arquería; Nuevas Consideraciones. ni en los modelos 1,2,y 3 anteriores.
En el mundo real
flecha, cuerda y el propio arco pesan, luego presentan inercia a su
movimiento,
una inercia proporcional a su peso (ya que los físicos
descubrieron hace tiempo que la masa gravitatoria es igual a la masa inerte). Todo ese peso combinado es el que la
elasticidad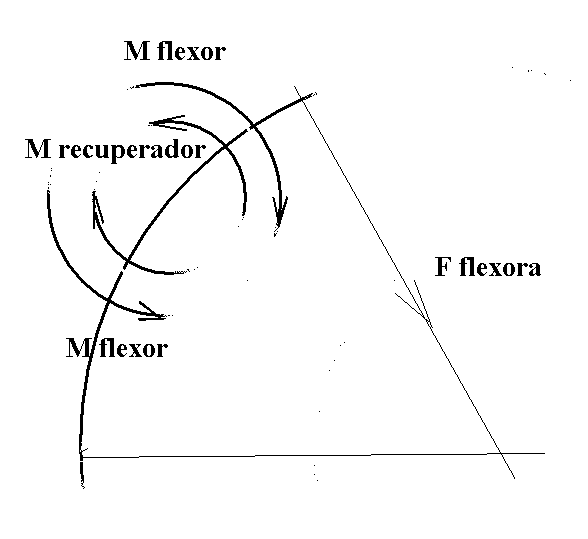 
del arco debe vencer, y ya se comprende que de ser alto el peso,
la velocidad final debe ser menor. Incluso el rozamiento del aire, dependiente
de la velocidad del cuerpo móvil (el arco en este caso) en su seno, se añade como fuerza opuesta al
avance. Por otra parte la fuerza de inercia (igual a la masa inerte por la
aceleración a que se somete) actúa diferentemente en las diversas partes del
arco, el cual se curva por ello diferentemente en cada parte.
La primera consideración, pues, es que el arco al enderezarse, debe arrastrar tres objetos, y de diferente manera:
la flecha, longitudinalmente la cuerda, transversalmente el propio arco (especialmente las palas si se fija el centro), transversalmente.
El poder enderezador del arco se debe a su elasticidad: en efecto, el arco tensado está flexando un material elástico, cuya fuerza de recuperación depende de varios factores
1. Del material y forma (curvatura inicial) de la pala del arco. 2. Del grosor de la pala del arco3. De la anchura de la pala del arco 4. De la masa o peso del arco.en el plano de su flexión, es decir, de delante atrás, lo que llamaríamos el grosor de la pala. Esto se veía en Txalaparta: breve estudio ... . en donde hallábamos que3. El sonido es más agudo cuanto más gruesa ... es la tabla, lo que a primera vista sorprende. Pero se entiende al recordar que cuanto más gruesa, más resistente es a la flexión, y la fuerza de recuperación es mayor.
Flexión del arco
Es decir, fijadas una forma y material del arco vibrante ‒las palas‒ es su grosor el que determina su poder recuperador, de enderezamiento, que mediremos como su aceleración de enderezamiento. Como eso depende de la flexión local, es decir, en cada punto, el problema es complicado. Porque es variable incluso si la grosor es uniforme, porque las fuerzas de tensión proceden todas de la cuerda atada al extremo de cada pala.
Solucionamos esta complicación considerando un arco ya flexado: por estar inmóvil, todas las fuerzas que s actúan sobre él están en equilibrio. las fuerzas son:
1. 'Una fuerza que pasa por el extremo donde se ata la cuerda (la parte de pala que excede ese atado es inoperante en la flexión, sólo añade peso muerto al arco.
2. La fuerza de recuperación en cada punto.
Podemos considerar dos momentos flectores en cada punto del arco:
1. El flector, positivo, de la cuerda que tira de los extremos de l arco.
2. El recuperador, debido a la elasticidad del arco.
(Está claro que un material no elástico, plástico, queda flexado y no recupera.)
Estos dos momentos son iguales y contrarios en cada punto del arco, porque
si no, se movería, se flexaría más o menor. La fo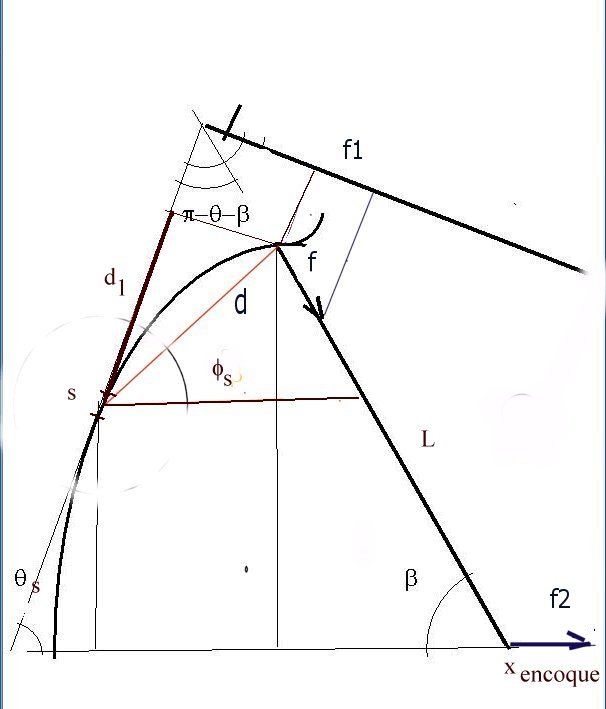
rma resultante es la
consecuencia de todos esos mementos equilibrados.. Y esto en cualquier
momento del tensado del arco, si se hace despacio, como es normal.
Veamos ahora el valor de esos momentos. Para ello emplearemos el modelo de la flexión simple, aproximado para pequeñas curvaturas (que se describe en Timoshebko, p zzz, y Morley, p yyy)
El momento flector de la fuerza F respecto al elemento de arco s es igual al producto del módulo (valor absoluto) de la fuerza por su distancia al elemento, es decir, por la distancia de s a la recta que contiene a la fuerza (es un vector deslizante).
Considerando al triángulo formado por los puntos coincidentes con el elemento s, con el extremos del último elemento del arco donde se ata la cuerda), y la intersección de la paralela a la flecha que pasa por s con la cuerda, tenemos que su ángulo superior vale 180º menos Beta y menos FIs. De modo que proyectando la distancia puntual d sobre la perpendicular a la cuerda que pasa por s, tenemos que la distancia buscada vale d por el coseno de ese ángulo. Luego
d1 = d . sin ( b + fs )
El paréntesis es un ángulo limitado superiormente: b+fs está limitado entre p,, para tensión pequeña, aunque siempre el arco curvado a la derecha; y p / 2, para gran tensión; incluso menor, exagerando ésta. Por lo tanto el seno de ese ángulo está a su vez limitado entre 0 y 1 aproximadamente.
El momento flector es pues:
M = f . d. sin ( b + fs )
y como contamos con la expresión general del ángulo de flexión en el elemento de arco de longitud S:
as = M.S/EI
donde
E (véase Elasticidad y vibracion) es el módulo de elasticidad o módulo de Young, ligada a la rigidez o fortaleza del arco. Se conoce como Rigidez el producto EI. Su sentido es claro: el ángulo girado es tanto menor cuanto mayor es la rigidez EI
I, momento de inercia de una sección recta rectangular de anchura b y grosor h es:
I = b.h^3/12
cuyo sentido intuitivo es la eficacia en un giro.; en nuestro caso con una flexión; con lo que tenemos:
as = (12/E ) . f1 d1 / (b.h^3)
cuyas dimensiones son (F L ) L / ( F L-2 L4) = L4 L-4 = adimensional, es un ángulo
En cuanto a la fuerza sagital (en dirección a la flecha) f2 que ejerce brazo-mano-dedos sobre la cuerda, y que es parcialmente transmitida por la cuerda para causar f, vale evidentemente:
f2 = 2. f . cos (b )
donde el factor 2 corresponde a que f2 se divide en 2 partes iguales, una por pala, por lo que debe ser doble que para una sola.
Pero f, fuerza a lo largo de la cuerda, puede considerarse como la resultante de otras dos: la citada Fuerza sagital horizontal, y otra vertical que coincide con la Fuerza que tensa el arco al encordarlo y so.
El arco está generalmente pre-flexado o pretensado, es decir, flexado antes de tirar de él. De modo que para conseguir esa fuerza de ángulo de la cuerda, beta, hay que componer esas dos fuerzas, y la sagital a ejercer será tanto mayor cuanto mayor es la pretensión. Claro que se alcanza en ese caso una mayor fuerza de flexado y por tanto más energía acumulada. Véanse estas fuerzas en Fuerzas en el arco.
¿¿¿¿p????
Cabe pues preguntarse cual es esa p cuales son las condiciones óptimas para que la fuerza ejercida tenga un alto rendimiento energético, el `problema que estudiamos en Rendimiento optimo de la fuerza ejercida.
Así que podemos calcular el conjuntos de puntos de la función f2 = f2 ( x2 ), Fuerza efectuada sobre la cuerda. en relación con la distancia de encoque al apoyo en el arco, función que acaba cuando esa distancia alcanza la longitud de la flecha. Esa función parece evidentemente creciente, mínima para el arco sin tensar y máxima para la distancia igual a la flecha. Pero veremos que esto no es del todo cierto para todos los diseños de pala.
Podemos encontrar empíricamente la función para cada arco, colgando el arco por su centro y colgando pesos crecientes del punto de la cuerda donde se inserta la flecha, midiendo los pares de valores Peso colgado-distancia. Así se hace en Energía almacenada en arco.. Aunque en este experimento la gravedad que afecta a las palas está dirigida diferentemente que en el tiro normal.
Fuerzas longitudinales
Hasta ahora henos despreciado las componentes paralelas a cada tramo.. Veámoslas en detalle en página aparte, Fuerzas longitudinales..
Implementación informática.
En nuestro programa Arco7, escrito en VisualBasic, realizamos el modelo anterior con el siguiente secuencia de operaciones.
1. Determinamos para las palas varios variables, tomando valores en cada una de las secciones en que dividimos su longitud. Las variables son: anchura, grosor, densidad, y módulo de elasticidad, E.
De ellas deducimos el momento de inercia de cada sector, lo que nos permite encontrar el ángulo Teta que el sector se curva, el cual ángulo deducimos, conocida la longitud del tramo, el radio de giro de la pala en ese tramo., una vez conocido el momento flector que experimenta por efecto de la fuerza que opera en el extremo de la pala.
Pero el momento depende de la fuerza y dirección de esa fuerza, y la dirección depende a su vez de la posición (coordenadas) del extremo de la pala respecto al horizontal, o mejor, respecto al eje donde se coloca la flecha.
Como esa posición depende de la curvatura que experimenta cada trama y la curvatura depende el momento que lo hace de la posición, nos encontramos con una dependencia circular que resolveremos mediante una iteración que ajuste progresivamente los valores de todas esas variable y funciones de ellas. Es decir, esperamos ese ajuste y esa convergencia.
De modo que, para cada fuerza ejercida sobre la flecha, elegimos una posición de extremo de pala, de ella un ángulo Beta, de ese ángulo y de la fuerza un momento en cada tramo, de su efecto acumulado desde el extremo fijo una posición de extremo resultante, de ella otro ángulo, ya que este depende de la longitud fija de cuerda, repetimos el cálculo de momento y así hasta que los valores de la posición, por ejemplo, no varías.
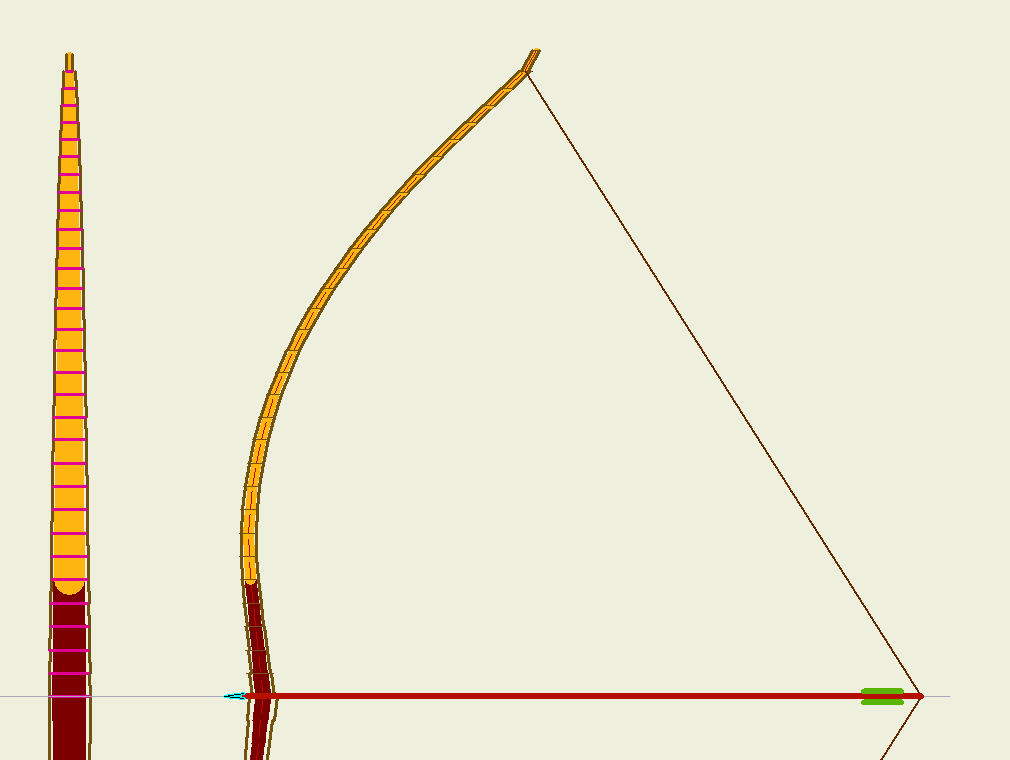
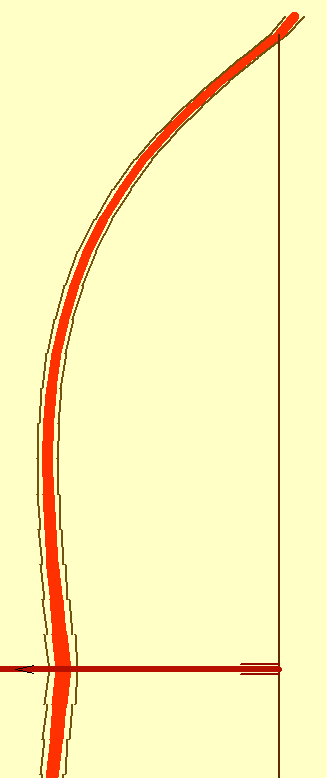
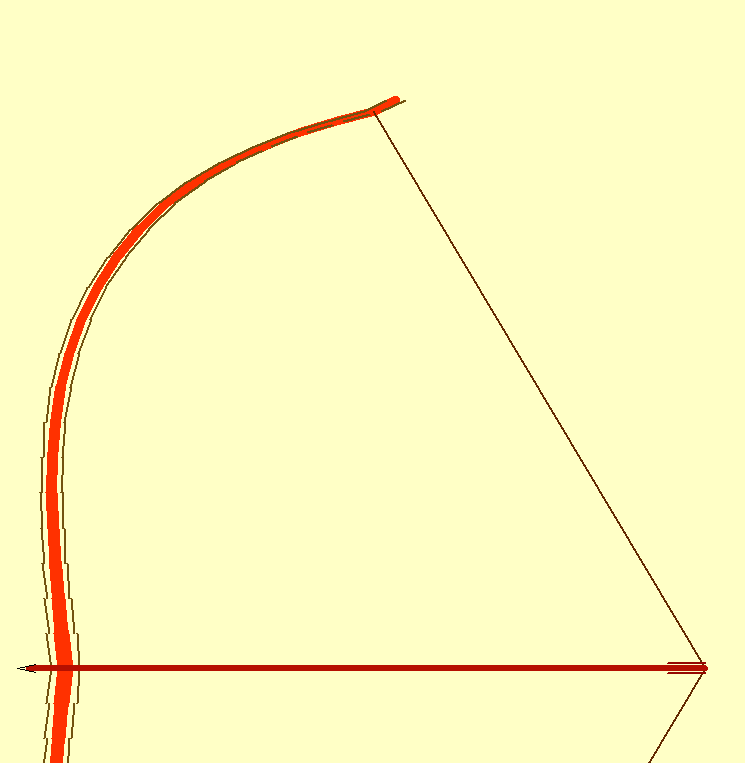
Un primer resultado es el que se muestra en la figura:
 |
 |
|
| Simulación de la flexión de un arco de sección y anchura variables. Puntos inicial y final. Fuerza siempre normal a arco incluso curvado. | ||
 |
 |
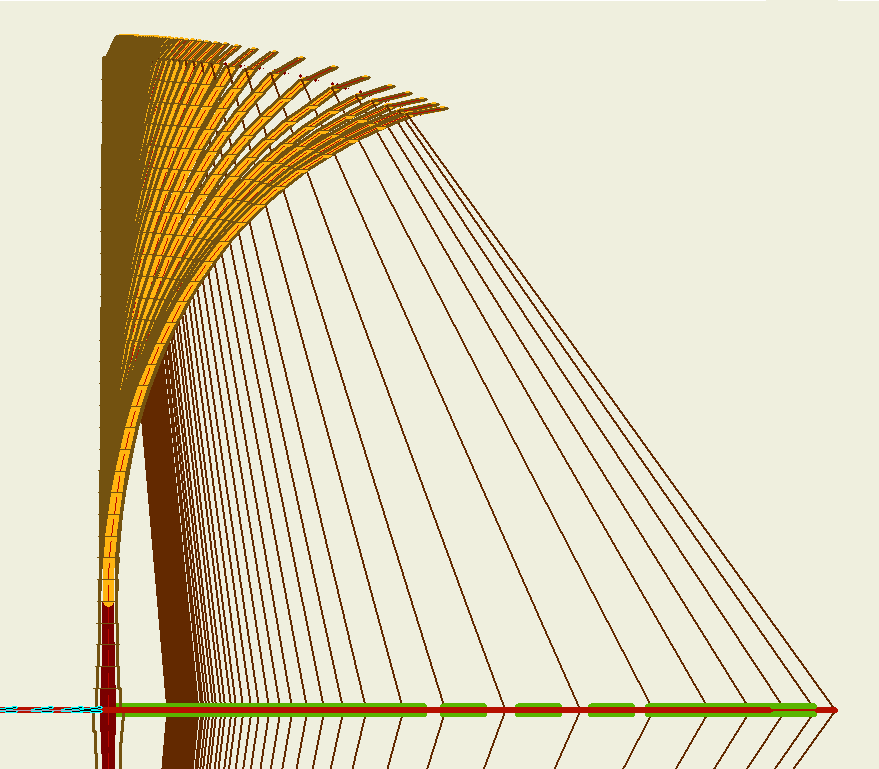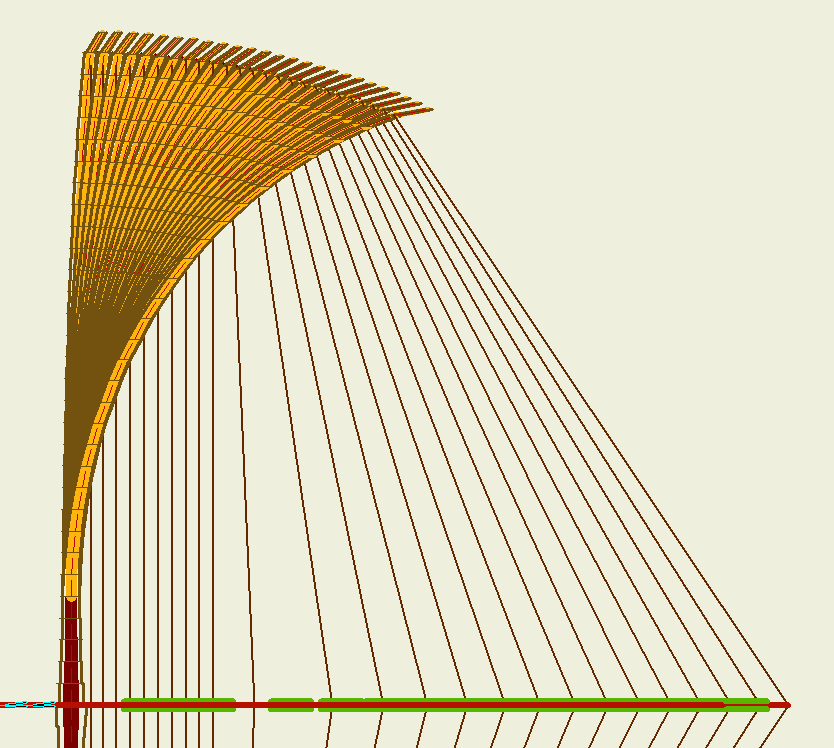
| Evolución de la tensión del arco para los modelos 1 y 2 |
Vea ahora Energía almacenada en arco y Energía almacenada.
Vuelta al Principio
Última
actualización:
viernes, 25 de mayo de 2018
Visitantes: