Fuerzas en el arco (forma parte de Arqueria)
Las fuerzas que actúan en el arco,
variables al encordar y al tensar, no
son fáciles de comprender a primera vista (al menos esto nos
ocurrió a nosotros, dotados quizá
de un pobre intelecto). Sin embargo, nos guía la experiencia de
hacerlo y sentir al tiempo la experiencia avasalladora del esfuerzo
realizado en los diferentes estadios citados.
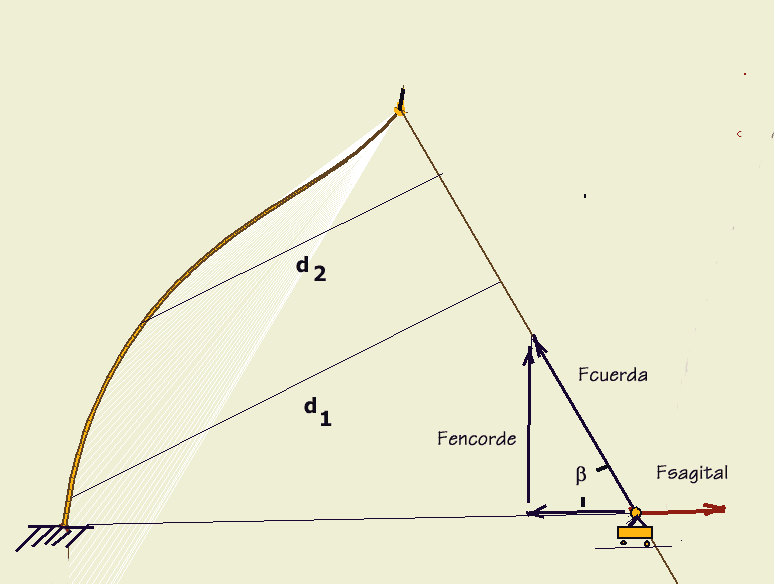
Lo primero que hemos de hacer es considerar sólo una mitad del arco; es evidente por simetría que a palas iguales los esfuerzos son siempre simétricos. El centro del cuerpo no se mueve pues durante la tensión, al tirar de la fuerza. Al encordar las palas desean recobrar su posición inicial y tiran de la cuerda hacia arriba con una fuerza de encorde que llamamos Fenc. La cuerda tira hacia abajo con fuerza igual, lo que mantiene el equilibrio. Al empezar a tirar de la cuerda para tensar el arco ejercemos una pequeña fuerza horizontal (en sentido de la flecha, mejor dicho, sagital), que llamamos Fsag. Esta fuerza se compone con Fenc mediante el paralelogramo de fuerzas con la diagonal como resultante. Ahora bien, para que el arco y cuerda sigan en equilibrio, la posición de la cuerda debe seguir esa diagonal, porque de otra manera se movería, giraría. Así que la magnitud relativa de esas cuerdas debe dar a lugar a esa inclinación, el ángulo b, que pasa de 90º, p /2, hasta un valor algo menor. Se cumple pues. siempre
Fsag + Fcuer_proy_sag = 0
es decir
Fcuer. cos b = Fsag
El momento que ejerce sobre un punto del arco es igual a esa fuerza en la cuerda, Fcuer , multiplicada por la distancia de ese elemento a la recta de la cuerda.
Ms = Fcuer . dsc
***
Se ve así como el encorde a tensión permite tensar el arco con mucha más
fuerza que sin él, ya que Fsag es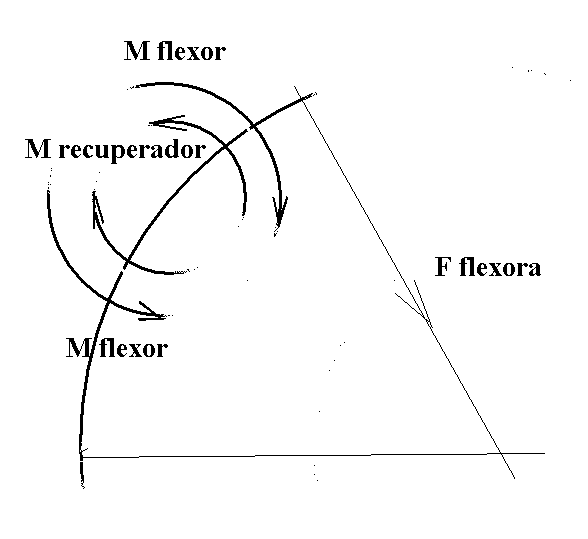
proporcional a ella. Esa fuerza Fenc la producen tanto el recurvamiento inverso
típico de los arcos actuales como el uso de una cuerda más corta que la
distancia en reposo entre puntos de encorde, como es evidente. Ese momento
es el que obliga a cada elemento de arco a flexar, según se muestra en
Elasticidad y flexion.
***
La fórmula anterior nos proporciona ya mucha información sobre el aprovechamiento de las fuerzas en el arco. Nos dice que para cada elemento de longitud s del arco, la fuerza produce tanto más momento, momento flector, cuanto mayor es la distancia de la recta de la fuerza al elemento, considerado como un punto. De modo que es la posición de la cuerda la que determina esa distancia a todos los s. Y esa distancia es máxima para la cuerda perpendicular (colectivamente perpendicular al arco. Mejor aún el ángulo beta debería ser tal que la cuerda debería formar un triángulo aproximadamente isósceles con arco (considerado recto) y flecha.
En ese punto la s distancias son aproximadamente máximas y por tanto los momentos y las flexiones subsiguientes: la fuerza sobre la cuerda es máximamente efectiva. Quede este punto para ser cotejado con otros muchos hasta llegar a un compromiso.
También aparece aquí explicado que al comenzar a tensar la fuerza cordal (en la cuerda) se hace rápidamente muy eficiente para formar memeonto flector puesto que se aleja rápidamente del arco en general con lo que los vbraz de l momento crecen deprisa. Esto puede incluso hacer disminuir la fuerza cordal a medida que tensamos, un resultado aparentemente paradógico.
Vuelta al
Principio
Última
actualización:
Thursday, 21 de February de 2013 Visitantes: