Esta página está en construcción: perdonen los errores y temas inacabados.

This page is being developed: I am sorry for errors and unfinished subjects.

ENEGRAMAS

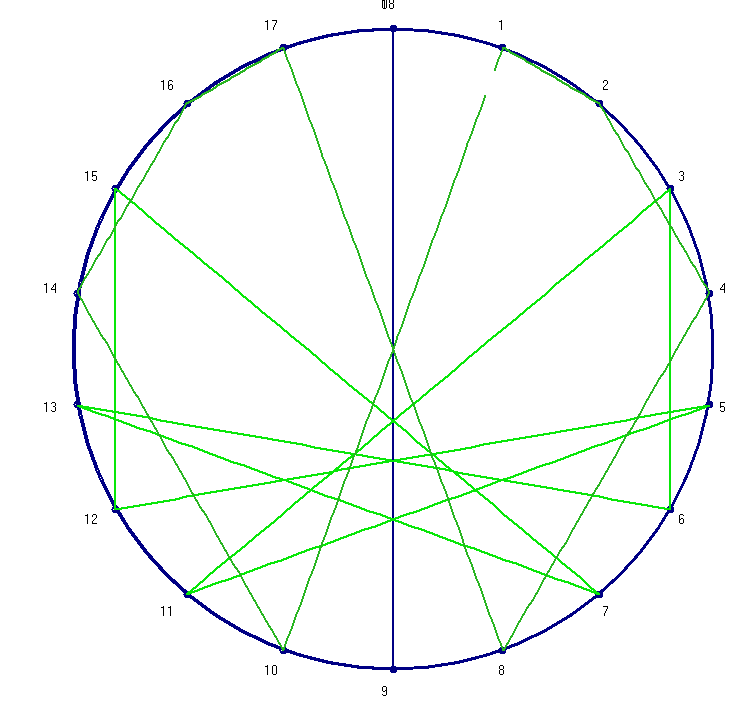
Este artículo trata sobre representaciones gráficas sobre la circunferencia de los períodos de las fracciones periódicas obtenidas al dividir enteros en diferentes bases de numeración. El trabajo está inspirado en el Eneagrama, un antiguo símbolo esotérico introducido en Occidente por el místico georgiano Gurdieff, que representa el período de los cocientes sucesivos al dividir 1 entre 7, en base 10, y al que se atribuyen cualidades extraordinarias para reflejar y poner de manifiesto el funcionamiento íntimo de las cosas. Sin entrar en esas interpretaciones esotéricas, aquí generalizamos esta representación a otros denominadores y bases, encontrándonos con una interesante familia de imágenes que plasman bellamente las propiedades de la división de enteros, especialmente la de sus periodos de cocientes y restos.

Basados en el Eneagrama, presentamos:

Los enegramas

Generalizando las representación anterior a otros denominadores y a otras Bases de numeración,, encontramos una serie de figuras que muestran una gran similitud, cualesquiera que sean los tamaños de b y n, pero dependiendo especialmente de su diferencia, según puede verse en las figuras contiguas. Estas figuras serán estudiadas más adelante. y las llamamos en general Pseudocardioides 2.

Escribimos un programa,, ENEA, para realizar estos dibujos.

Enegrama para 137 en base 139. Restos.	Enegrama para 1137 en base 1139. Cocientes


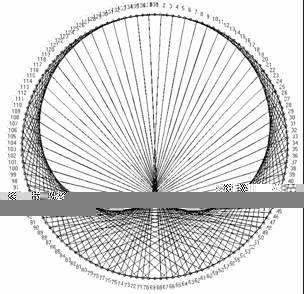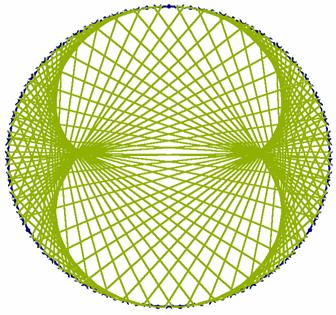Enegrama para 137 en base 140 Cocientes

Períodos de Restos y de Cocientes

Tienen una estrecha relación, no sólo la obvia de mutua dependencia, sino que son casi iguales, y su desigualdad se produce de manera simétrica y regular. En efecto, cualquier cociente c_i puede obtenerse de su correspondiente resto r_i mediante la expresión 10* r_i = c_i * n + r_i+1 que procede del algoritmo de la división.

Equivalentemente podemos escribir: 10 * r_i / n = c_i + r_i+1/ n, o bien c_i = 10 / n * r_i - r_i+1/ n.

Si n < 10, escribimos c_i = (1 + (10-n)) / n * r_i - r_i+1/ n. = (r_i + r_i* (10-n)) / n _i - r_i+1/ n.

Apliquemos esto al cociente 1/7: se nos producen las siguientes igualdades sucesivas:

1 * 10 = 1 * 7 + 3

3 * 10 = 4 * 7 + 2

2 * 10 = 2 * 7 + 3

1 = 1 * 10 / 7 - 3 / 7

4 = 3 * 10 / 7 - 2 / 7

2 = 2 * 10 / 7 - 3 / 7

1 = 1 + 1* 3 / 7 - 3 / 7

4 = 3 + 3 * 3 / 7 - 2 / 7

2 = 2 + 2 * 3 / 7 - 3 / 7

donde encontramos que el cociente es igual que el resto cuando ese resto multiplicado por la razón constante (10-7)/7=3/7 es menor que 1, siendo una unidad mayor cuando es igual (no en este caso) o mayor que 1, y menor que 2, o dos unidades mayor cuando es mayor que dos y menor que tres, y así sucesivamente; la relación entre resto y cociente viene pues regulada por el valor del cociente entero (b-n)/n.

Los propios restos dependen estrechamente de ese mismo valor: en efecto, podemos escribir las expresiones anteriores de otra manera:

r_i+1 = c_i * n + b* r _i = c_i * n + b* r _i + n* r _i - n* r _i = ( c_i+ r _i ) * n +(b - n)* r _i (2)

es decir, que puede obtenerse un resto cualquiera multiplicando el anterior por el valor –o módulo– (b-n). Este proceso se prolonga mientras el producto (b - n)* r _i es menor que n, ya que en ese momento el primer sumando de la expresión (2) admite una unidad más, quedando:

r_i+1 = ( c_i+ r _i +1 ) * n + (b - n)* r _i - n = ( c_i+ r _i +1 ) * n + ((b - n-1)* r _i) (3)

y sucesivamente:

r_i+1 = ( c_i+ r _i+1 ) * n + (b - n)* r _i- n = ( c_i+ r _i +r _i* mod n )* n + ((b - n)*r _i) mod n (4)

Véase el caso anterior en que b-n=3, y cómo los restos siguen la sucesión: 1, 3, 3², 3³, 3⁴, 3⁵, 3⁶, que queda, al aplicar el módulo 7: 1, 3, 2, 6, 4, 5...

Esta propiedad permite predecir el valor de un resto cualquiera sin efectuar la división; en efecto:

r_i+1 =(b - n)ⁱ mod n (5)

interesante expresión –cuyo interés no mengua aunque el cálculo de ese resto sea quizá más sencillo dividiendo. Nótese que los restos –y por tanto los cocientes– no siguen una sucesión errática o misteriosa, como el escolar ingenuo pudiera creer, sino que ambos están perfectamente determinados –esto es obvio– y son predecibles sin calcular los anteriores –no tan obvio.

Los restos siguen así un camino sobre la circunferencia según las potencias del valor c = (b-n) hasta que se cierra una vuelta completa –o aplicación del módulo n, comenzando una subsucesión cuyos términos cumplen la expresión, pero tomando un valor inicial diferente, precisamente el dado por (4).

Longitud de la serie de cocientes

Volveremos al principio cuando lleguemos a un resto igual al primero; en ese momento obtenemos una secuencia cuya longitud vamos a investigar. Se trata de ver cuándo la suma de potencias de d = b-n alcanza el primer valor, es decir, cuándo

r_i+1 = (b - n)ⁱ mod n (6)

o sea,

r_i+1 = dⁱ + N n (6')

o sea, se trata de calcular la suma de los k términos de una progresión geométrica de razón d, y primer término 1 (???).

S_n= a₁ (d^k - 1) / (d -1 )

y esta suma vuelve a 'cerrar' la curva cuando vuelve a coincidir un cociente, al cabo de un número de vueltas N, desconocido.. De modo que:

(d^k - 1) / (d -1 ) = N n o sea d^k = 1 + N n ( d-1) con lo que

k = ln (1 + N n ( d-1) ) / ln (d) (6'')

donde ln es el logaritmo neperiano (aunque cualquier otro vale igualmente). Es decir, k es la longitud de la sucesión de cocientes tras un número de vueltas N. A su vez, N es el número mínimo que hace k entero (naturalmente lo es porque es un número de cocientes, un cardinal). De modo que en cada caso de d y b hay que probar uno a uno comenzando en 1. A su vez:

N = ( d^k - 1 ) / b ( d-1))

es decir, podemos buscar el k que hace N entero, pero es mucho más corto probar con la fórmula anterior.

Refinamiento del cálculo de la longitud

Por ejemplo en la sucesión de restos de 1/17 en base 20, tenemos igualmente que c = b-n = 3, con lo que la sucesión será: 1, 3, 9, (27<>)10, (30<>) 13, (39<>) 5, 15, (45<>) 11, ... hasta llegar otra vez al primero, cerrándose el ciclo de restos o período, con una longitud de 16 cifras en este caso.

Es decir (siempre en este caso), que cuando d elevado a la longitud del período es 1, es decir, un número congruente con 1 ( n::1 ), se cierra el período. Este hecho nos proporciona una sencilla regla de encontrar esa longitud L(p_n):

La longitud del período de restos es el menor exponente (mayor que 0) que verifica

(b - n) ^L(pn⁾ :: 1 (7)

regla más sencilla con frecuencia que la usual:

b ^L(pn⁾ :: 1 (8)

(compárense las potencias 3 ¹⁶ con 20 ¹⁶⁾ para comprobarlo.

Si b y n son muy diferentes, pueden emplearse otras expresiones similares aún más sencillas; es decir, a partir de (6):

(b - n) ^{L ( p}_n⁾ = 1 + k . n (9)

L(p_n) = ln (1 + kn ) / ln(b-n ) (10)

Siendo k el menor entero que proporciona L entero.

Por ejemplo el período de 1/1137 en base 1140; k es el menor entero que hace L entero, con c=1140-1137=3: L = ln (1+k.1137) / ln(3): vamos probando:

k 1 2 3 4 5 6 7 8 9

L 6.4 7.03 7.4 ....

Series de Cocientes

La expresión (4) nos permite deducir igualmente la sucesión de cocientes a partir de la restos:

En efecto, esta nueva sucesión es igual a la de restos excepto que el cociente homólogo de un resto aumenta en tantas unidades como se aplica el modulo n al resto correspondiente: es decir:

(continúa)

Información empírica

Para 17 en base 20 y para 137 en base 139, y para numeradores sucesivos empezando en 1, reproducimos la información proporcionada por nuestro programa Wenea04, que consiste en los siguientes ítems:

1. El cociente m/n (base), con los numeradores creciendo de 1 a n-1.

2. Serie de cocientes, codificando cada uno con una cifra, un carácter alfanumérico ASCII, en la cual puede verse la reaparición del período. Se separa la serie en grupos de 10, separados por comas.

3. La misma serie de cocientes, pero codificados en base 10: se escribe cada cociente en columna, unidades abajo, decenas encima y así sucesivamente. Todos esos números son naturalmente menores que el denominador.

4. Cifras que no aparecen en esa serie.

5. Período de la serie de cocientes, encontrado empíricamente por comparación.

6. Longitud de ese período (número de cifras). Longitud teórica, aplicando la fórmula:

7. Primeras diferencias entre cifras continuas.

8. Las mismas diferencias, codificados en columna.

En las tablas siguientes pueden verse los casos 17//20 y 137//140

PRIMEROS COCIENTES Y RESTOS DEL DIVISOR 17 EN BASE 20 Y SU ENEGRAMA

1 / 17  (20) 
 COCIENTES:     .13ABF5HCIG,984E27.13
       10^1        111 1111,   1  
       10^0      1301557286,984427

 VACÍO PARCIAL:  6DJ   
 PERIODO:       
 LONGITUD:    ( 16 )  TEO: ( 13 ) 
 SUMA MITAD C:  19 )  JJJJJJJJ  ( 19)     
 DIFERENCIAS:    127147CC6F,AGDA55
       10^1            11 1,1111  
       10^0      1271472265,063055

 RESTOS:        .139AD5FBGE,874C26.13     
       10^1         11 1111,   1  
       10^0      1390355164,874226

 SUMA MITAD R:    ( 17 )HHHHHHHH (17)     
 NORMALIZO  
       10^1       155728698,442713
       10^0      6839698542,714125

 2 / 17  (20) 
 COCIENTES:     .2713ABF5HC,IG984E.27
       10^1          111 11,11   1
       10^0      2713015572,869844

 VACÍO PARCIAL:  6DJ   
 PERIODO:       
 LONGITUD:      ( 16 ) TEO:    ( 13) 
 SUMA MITAD C:    ( 19 )JJJJJJJJ (19)     
 DIFERENCIAS:    25B27147CC,6FAGDA
       10^1        1     11, 11111
       10^0      2512714722,650630

 RESTOS:        .26139AD5FB,GE874C.26     
       10^1           11 11,11   1
       10^0      2613903551,648742

 SUMA MITAD R:    ( 17 )HHHHHHHH ( 17)     
 NORMALIZO  
       10^1      13 1557286,984427
       10^0      2568396985,427141

 3 / 17  (20) 
 COCIENTES:     .3ABF5HCIG9,84E271.3A
       10^1       111 1111 ,  1   
       10^0      3015572869,844271

  VACÍO PARCIAL:  6DJ   
 PERIODO:       
 LONGITUD:      ( 16 )  TEO:( 13 ) 
 SUMA MITAD C:    ( 19 )JJJJJJJJ (19)     
 DIFERENCIAS:    37147CC6FA,GDA55B
       10^1           11 11,111  1
       10^0      3714722650,630551

 RESTOS:        .39AD5FBGE8,74C261.39     
       10^1        11 1111 ,  1   
       10^0      3903551648,742261

 SUMA MITAD R:    ( 17 )HHHHHHHH (17)     
 NORMALIZO  
       10^1       1    111 ,1111  
       10^0      4427130155,728698

E N E A G R A M A S G E N E R A L I Z A D O S

1 / 137 (139)

COCIENTES: .1248GWwëâ,xíæØ‰Piœvé,Þ•hšrá›tåÖ,…HY{óòðìäÔ,9I[€7ESoÛ,

Coc: \‚BMc^†J,]„FUsãŸ}12,48GWwëâxí,æØ‰PiœvéÞ•,hšrá›tåÖ…H,

Coc: Y{óòðìäÔ9,I[€7ESoÛ\,‚BMc^†J]„,FUsãŸ}.12

10^2 111, 111 1 1,1 11 11, 111111, 1,

10^1 136220,6321825062,1949510620,7136333320,7 137 1251,8

10^0 1248624902,5140250137,6499990138,8748764026,4986374863,8

10^2 0 , 11 , 111 1,11 1 11 , 11 11 ,

10^1 8371248371,37136207 , 13622063,2182506219,4951062071,3

10^0 8751249999,8750014012,4862490251,4025013764,9999013887,4

10^2 0 111111 , 1 , , 11

10^1 363333207 ,137 125183,7124837137,136207

10^0 4876402649,8637486387,5124999987,500140

VACÍO PARCIAL: 356A,CDK,LNOQRTVXZ_,`abdefgjklmnpquyz|~ƒ‡,ˆŠ‹ŒŽ‘,’“”–—˜™ž Õ×ÙÚÜÝßàçèêîïñô

PERIODO: 1248GWwëâ,xíæØ‰Piœvé,Þ•hšrá›tåÖ,…HY{óòðìäÔ,9I[€7ESoÛ,

Par: \‚BMc^†J,]„FUsãŸ}

LONGITUD: ( 68 ) LONGITU TEO: ( 9 )

SUMA MITAD C: ( 138 )ôôôôôôôôôô,ôôôôôôôôôô,ôôôôôôôôôô,ôôôô ( 138 )

DIFERENCIAS: 11248GWxêá,›yìå×‡Pjšw,èÝ“i˜sà™uä,ÕƒHY|òñïëã, 9I\~7ESp,

dif: Ú]€BMdŽ_„,J^‚FUtâž{1,248GWxêá›y,ìå×‡PjšwèÝ,“i˜sà™uäÕƒ,

dif: HY|òñïëã ,9I\~7ESpÚ,]€BMdŽ_„J^,‚FUtâž

10^2 11,1 111 ,11 1 1,1 11111,1 ,1

10^1 13621,0632082596,2195961962,0713633322,07 137 125,1

10^0 1124862589,0603905194,6520708822,7674965391,5298717487,2

10^2 1 , 11 , 111 ,111 11, 1 11 ,

10^1 1837124847,137136206 , 1362106,3208259621,9596196207,1

10^0 2683125707,9955010381,2486258906,0390519465,2070882276,7

10^2 0 111111 , 1 , , 11

10^1 1363332207, 137 12518,3712484713,713620

10^0 7496539152,9871748726,8312570799,550103

RESTOS: .1248GWwêáœ,xìå×ˆPi›vè,Ý”h™ràštäÕ,„HY{òñïëã ,€9I[7ESoÚ,

Res: Ž\BMc^…J,]ƒFUsâž|12,48GWwêáœxì,å×ˆPi›vèÝ”,h™ràštäÕ„H,

Res: Y{òñïëã €9,I[7ESoÚŽ\,BMc^…J]ƒ,FUsâž|.12

10^2 111, 111 1 1,1 1 11, 111111, 1,

10^1 136210,6320825062,1949519620,7136333220,7 137 1251,8

10^0 1248624891,5039150036,5398989127,7748653915,3986274862,7

10^2 0 , 11 , 111 1,11 1 11 , 1 11 ,

10^1 8371248371,37136206 , 13621063,2082506219,4951962071,3

10^0 7741248989,8650003912,4862489150,3915003653,9898912777,4

10^2 0 111111 , 1 , , 11

10^1 363332207 ,137 125183,7124837137,136206

10^0 4865391539,8627486277,4124898986,500039

SUMA MITAD R: ( 137 )óóóóóóóóóó,óóóóóóóóóó,óóóóóóóóóó,óóóó ( 137 )

NORMALIZO

10^1 124987,4998513749,8637487487,5125999987,5 125 1248,6

10^0 1136237374,7500986362,4862362598,6250997487,3736350012,4

10^1 625 136251,25124875 , 12498749,9851374986,3748748751,2

10^0 4748624874,8512485011,3623737475,0098636248,6236259862,5

10^1 2599998750,1250124862,5013625125,124875

10^0 5099748737,3635001247,4862487485,124850

10^0 0997487373,6350012474,8624874851,248501

2 / 137 (139)

COCIENTES: .248GWwëâx,íæØ‰PiœvéÞ,•hšrá›tåÖ…,HY{óòðìäÔ,9I[€7ESoÛ,

Coc: \‚BMc^†J],„FUsãŸ}124,8GWwëâxíæ,Ø‰PiœvéÞ•h,šrá›tåÖ…HY,

Coc: {óòðìäÔ9I,[€7ESoÛ\‚,BMc^†J]„F,UsãŸ}1.24

10^2 111 ,111 1 11, 11 11 , 111111 , 1 ,

10^1 1362206,3218250621,9495106207,1363333207, 137 12518,3

10^0 2486249025,1402501376,4999901388,7487640264,9863748638,7

10^2 0 , 11 , 111 11,1 1 11 , 11 11 ,

10^1 3712483713,7136207 , 136220632,1825062194,9510620713,6

10^0 7512499998,7500140124,8624902514,0250137649,9990138874,8

10^2 0111111 , 1 , , 11

10^1 63333207 1,37 1251837,1248371371,36207

10^0 8764026498,6374863875,1249999875,001401

VACÍO PARCIAL: 356A,CDK,LNOQRTVXZ_,`abdefgjklmnpquyz|~ƒ‡,ˆŠ‹ŒŽ‘,

’“”–—˜™ž Õ×ÙÚÜÝßàçèêîïñô

PERIODO: 248GWwëâx,íæØ‰PiœvéÞ,•hšrá›tåÖ…,HY{óòðìäÔ,9I[€7ESoÛ,

Par: \‚BMc^†J],„FUsãŸ}1

LONGITUD: ( 68 ) LONGITU TEO: ( 9 )

SUMA MITAD C: ( 138 )ôôôôôôôôôô,ôôôôôôôôôô,ôôôôôôôôôô,ôôôô ( 138 )

DIFERENCIAS: 2248GWxêá›,yìå×‡Pjšwè,Ý“i˜sà™uäÕ,ƒHY|òñïëã ,9I\~7ESpÚ,

dif: ]€BMdŽ_„J,^‚FUtâž{12,48GWxêá›yì,å×‡PjšwèÝ“,i˜sà™uäÕƒH,

dif: Y|òñïëã 9,I\~7ESpÚ],€BMdŽ_„J^‚,FUtâž{

10^2 111, 111 1,1 1 11, 111111, 1,

10^1 136210,6320825962,1959619620,7136333220,7 137 1251,8

10^0 2248625890,6039051946,5207088227,6749653915,2987174872,6

10^2 0 , 11 , 111 1,11 11 , 1 11 ,

10^1 8371248471,37136206 , 13621063,2082596219,5961962071,3

10^0 6831257079,9550103812,4862589060,3905194652,0708822767,4

10^2 0 111111 , 1 , , 11

10^1 363332207 ,137 125183,7124847137,136206

10^0 4965391529,8717487268,3125707995,501038

RESTOS: .248GWwêáœx,ìå×ˆPi›vèÝ,”h™ràštäÕ„,HY{òñïëã €,9I[7ESoÚŽ,

Res: \BMc^…J],ƒFUsâž|124,8GWwêáœxìå,×ˆPi›vèÝ”h,™ràštäÕ„HY,

Res: {òñïëã €9I,[7ESoÚŽ\,BMc^…J]ƒF,Usâž|1.24

10^2 111 ,111 1 11, 1 11 , 111111 , 1 ,

10^1 1362106,3208250621,9495196207,1363332207, 137 12518,3

10^0 2486248915,0391500365,3989891277,7486539153,9862748627,7

10^2 0 , 11 , 111 11,1 1 11 , 1 11 ,

10^1 3712483713,7136206 , 136210632,0825062194,9519620713,6

10^0 7412489898,6500039124,8624891503,9150036539,8989127774,8

10^2 0111111 , 1 , , 11

10^1 63332207 1,37 1251837,1248371371,36206

10^0 8653915398,6274862774,1248989865,000391

SUMA MITAD R: ( 137 )óóóóóóóóóó,óóóóóóóóóó,óóóóóóóóóó,óóóó ( 137 )

NORMALIZO

10^1 1249874,9985137498,6374874875,1259999875, 125 12486,2

10^0 1362373747,5009863624,8623625986,2509974873,7363500124,7

10^1 25 1362512,5124875 , 124987499,8513749863,7487487512,5

10^0 7486248748,5124850113,6237374750,0986362486,2362598625,0

10^1 5999987501,2501248625,0136251251,248750

10^0 0997487373,6350012474,8624874851,248501

Pseudocardioide

Otros diseños

Prolongaciones

Vuelta al Principio Última actualización: sábado, 14 de septiembre de 2013 Visitantes: