Esta página está en construcción: perdonen los errores y temas inacabados.
This page is being developed: I am sorry for errors and unfinished subjects.
El Eneagrama (forma parte de Enegramas)
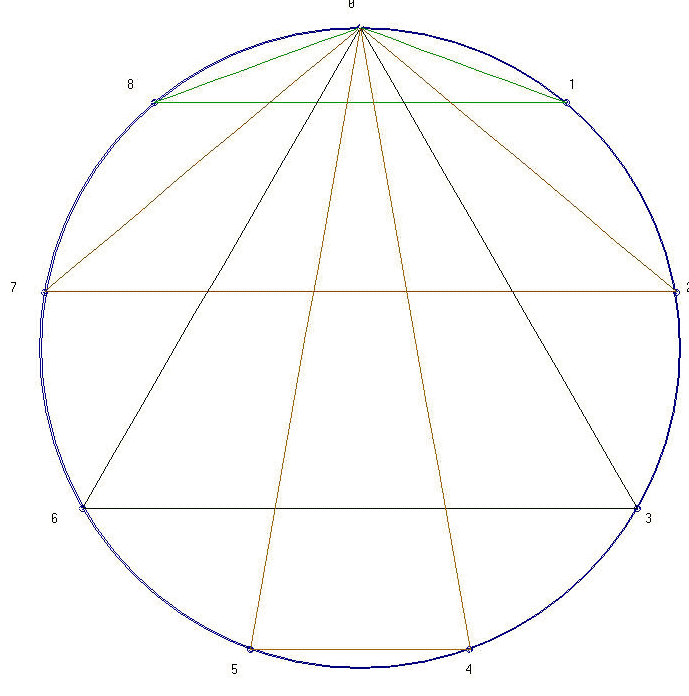
Es un símbolo que aparece ligado al místico Gurdjieff, y al cual se atribuyen propiedades ligadas al desarrollo espiritual. Se obtiene representando sobre una circunferencia los períodos de los cocientes entre 7 de los enteros menores que 7, atribuyendo a cada cociente en el algoritmo de la división un punto sobre la circunferencia, uno de los 10 posibles, de 0 a 9. Ahora bien, el cero no aparece en el periodo y no se lo representa como punto –aunque hay quien considera que la circunferencia es ese 0–, con lo que se colocan sólo 9 puntos, con el último en la posición más alta, y creciendo en el sentido de giro de las agujas del reloj. Uniendo los cocientes sucesivos encontramos un polígono de seis lados que cerramos con el período siguiente, con lo que podemos considerar que sigue moviéndose sin detenerse, recorriendo una y otra vez el hexágono, plegado, entre los puntos 142857.
En el período no aparecen los números 3, 6 y 9: son unidos entre sí con un nuevo polígono independiente, un triángulo equilátero de base horizontal, completándose así el este diagrama simbólico (que veremos más adelante).
El cociente por 7 de los sucesivos enteros menores que 7, da lugar a un período de igual longitud, 6, con las mismas cifras que 1:7 y en igual orden circular: 2/7 = 285714.28...
De modo que en todos ellos el eneagrama “se mueve” de igual manera, aunque comenzando en lugares diferentes
| 1 / 7 (10) COCIENTES: .142857.14 VACÍO PARCIAL: 369 PERIODO: ( 6 ) TEO:( 6 ) SUMA MITAD C: ( 9 ) 999 DIFERENCIAS: 135642 RESTOS: .132645.13 SUMA MITAD R: ( 7 ) 777 | 2 / 7 (10) COCIENTES: .285714.28 VACÍO PARCIAL: 369 PERIODO: ( 6 ) TEO:( 6 ) SUMA MITAD C: ( 9 )999 ( 9 ) DIFERENCIAS: 264213 RESTOS: .264513.26 SUMA MITAD R: ( 7 )777 |
| Tabla 1. Para cada numerador, se escribe el periodo de cocientes, los divisores no encontrados en él, las diferencias, el periodo de restos y las sumas de mitades del período. | |
 |
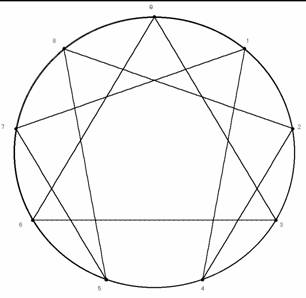 |
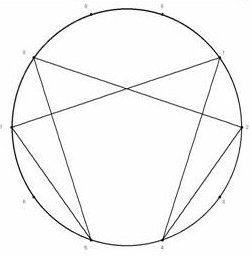
| Fig.2. Enegrama de m/7, representando el 0 | Fig.1. El Eneagrama, sin el 0 |