Esta página está en construcción: perdonen los errores y temas inacabados.

This page is being developed: I am sorry for errors and unfinished subjects.

ENEGRAMAS. Prolongaciones. (forma parte de Enegramas)

Prologamos los flecos de enegramas que van saliendo.

En busca de una posible sinestesia entre números y música, añadida a todas las ya vistas hemos dotado a nuestro programa Enea04 de sonido. He aquí el razonamiento que subyace en el posible capricho.

Comoquiera que tanto las escalas como los ritmos admiten una visión circular que se renueva a cada vuelta, estrictamente lo que produce las congruencias y la función 'módulo', hemos dotado al dibujo de aquellos de un sonido simultáneo ligado a los cocientes (o restos) que van apareciendo sobre la circunferencia. y cuyo tono corresponde a su posición angular de dos maneras opcionales: o el ángulo con el radio vertical superior representa un intervalo (medido en cents, por ejemplo), o bien representa un incremento de la frecuencia (medida en hercios por ejemplo), a partir de un arbitraria que corresponde

O seas la octava, el círculo, corresponde bien a 1200 cents o al doble de la frecuencia inicial. Oiga la secuencia correspondiente al par 17 - 19.

La primera es una cierta belleza que se desprende de todo esto, un conectar con la constitución de los números, viéndolos y oyéndolos, por decirlo así.

La segunda, ya sugerida a quienes se ocupan de estos temas, es la de generar secuencias aparentemente aleatorias pero totalmente deterministas una vez conocidos los enteros en juego: se trata de una división. Estas secuencias pueden usarse quizá para cifrar información, escrita o sonora, una vez garantizado el carácter amorfo de esa secuencia, ya que cualquier rasgo característico la haría identificable y por lo tanto descifrable. Este carácter amorfo puede comprobarse mediante una estadística de las cifras aparecidas, que debe demostrar una distribución uniforme para todas ellas. Asmismo deberían ser uniformes las distribuciones de pares contiguos, trios, etc.

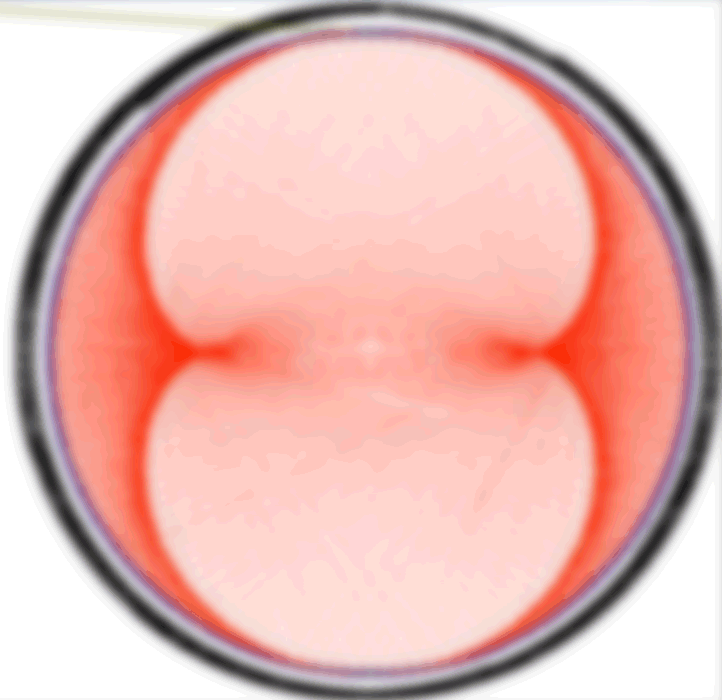1. Las cuerdas no se cruzan de manera sucesiva sino en diferentes 'vueltas'. Por lo tanto es el ojo quien dibuja las pseudocardioides, Lo mismo podemos decir de otras figuras que se nos aparecen al variar divisor y base de numeración. Las líneas que vemos son simples concentraciones de negror generadas por el paso de muchas líneas en ellas. Son como caminos realizados por miles de pies en sus paseos y marchas discontinuos. Son simplemente zonas de paso. Se producen estas zonas cuando los ángulos de intersección son pequeños.

Típicamente cuando ambas cuerdas tienen sus extremos cercanos dos a dos y precisamente en orden inverso. Por ejemplo:

En la figura contigua se ha filtrado la imagen ('paso bajo' para eliminar bordes,) subsistiendo el pseudocardioide en nuestra percepción).

2. Cuando las cuerdas no intersectan dentro del círculo, pueden hacerlo fuera. Hay que investigar ese exterior (infinito, por cierto, para asomarse al otro lado del espejo.

Nuestra intuición era pertinente: cuando no hay figura dentro del círculo, es decir, intersecciones, la figura pasa afuera., como muestra la figura, la primera que realizamos extrapolando las cuerdas fuera del circulo.

Vuelta al Principio Última actualización: Thursday, 21 de February de 2013 Visitantes:


Enegrama extrapolado de 137(133) d=b-n= -4:	Enegrama extrapolado de 237(234) d=b-n= -3:


Enegrama extrapolado de 123 (4321)