Arco/Elasticidad y flexión.htm

Acabamos de ver la tracción/compresión en Elasticidad y vibración y el importante modulo de Young. Apliquemos todo ello a la flexión. Más precisamente, a la llamada flexión simple: simple porque se hacen varias suposiciones simplificadoras para aplicar su teoría. Es aplicable en vigas o barras finas y largas, espesor menor que un décimo de la longitud para fijar un límite directo. Se supone que las secciones rectas antes de la flexión lo siguen siendo después de ésta; despreciamos por ahora las fuerzas de cortadura, fuerzas tangenciales a la fibra que flexa que intentan desplazar una capa respecto a la contigua.

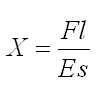
Vea ahora la aplicación de todo esto a la flexión.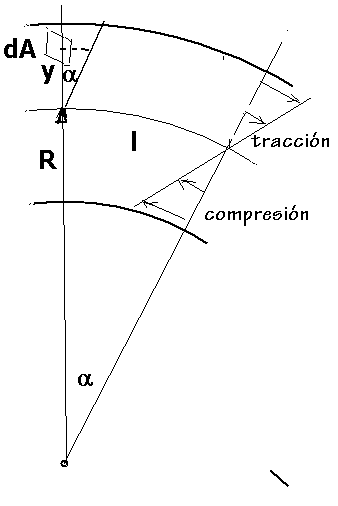 esa aplicación emplea una serie de hipótesis simplificadoras y recibe el nombre de flexión simple. La renuncia a alguna de esas hipótesis complica em modelo.

En ella sucede que las capas exteriores (alejadas del centro de curvatura) se expanden y las interiores se contraen. No puede ser de otra manera porque en ese caso la suma de las fuerzas no sería nula y el tramo flexado se movería en la dirección de la resultante, lo cual no ocurre porque estamos estudiando una posición de equilibrio, tensión flectora pero inmovilidad.

Así que debe haber una capa que no haga una cosa ni otra, la llamada capa neutra, línea neutra si consideramos su sección con el plano del dibujo. Consideramos este plano como el plano XY, X se mueve a lo largo de la viga, Y sobre su espesor. La perpendicular (sentido de la anchura de la viga es el eje Z. Consideramos ahora elementos de superficie en el plano YZ, los cuales están sipometidos a fuerzas de tracción y compresión, como decíamos, según de observa en el dibujo.

Aparece en este una elemento de longitud (eje X) sometido a flexión por un par de fuerzas de valor de momento M.

Por semejanza de triángulos:

L / R = y / X X / L = y / R

s = dA = b dy

F = X E b y / L = E b y y / R = b E y² / R

La suma de fuerzas es nula a lo largo de la sección, como se justificaba más arriba. De modo que

S d F = S (b dy )E y / R = (b E/ R) / S y dy = (b E/ 2R) (h₂²- h₁²) = 0

donde hemos tomado el sumatorio como una integral, que hemos operado entre las valores límites h₁, h₂de la ordenada y, cuyo origen es la capa neutra de deformación nula; esos valores tienen signo contrario por lo tanto.

.De modo que en valor absoluto, h₂ y h₁, distancias límites de las capas de la viga al plano neutro son iguales: ello equivale a decir que esta se encuentra en el centro de la viga: es una capa media. Todo ello, claro, para una sola capa, o sea, un solo material. Otro caso es el de las Laminas multicapa.

Atendiendo ahora a los momentos, podemos expresar la igualdad entre los valores absolutos del momento aplicado para flexionar y la suma de los momentos elementales resistentes que provienen de la material elástico que compone la viga o barra.

Esta igualdad es:

M = S d M = S y d F =S E b y² / R = (b E/ R) / S y² dy = (bE/ 3R) (h₂³- h₁³)

haciendo h₂= h₁= h

M = (b E/ 3R) (h₂³- h₁³)= (2b E/ (3.8.R) (h³)=E (b h³/ 12)/R = EI / R

donde aparece la expresión, sólo dependiente de la forma de la sección,

I = bh³/ 12

que es el llamado momento de inercia de la sección rectangular de la viga respecto a su capa neutra, en el centro para material homogéneo.

El producto EI es la llamada rigidez de la viga, dependiente de material (E) y forma de la sección.(I). Se simboliza a veces EI como J.

Podemos expresar la ecuación anterior, recordando que Ra = L, como

a = M L / E I

que expresa el ángulo girado en la flexión de un elemento de barra de longitud L y elasticidad E bajo la acción de un momento M.

En rigor esto sólo vale para un elemento corto de barra, en el que todo es constante: E, M e I. Más precisamente:

da = M d l / E I

y el ángulo total será

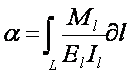
en la que cada elemento de longitud d l posee en general diferentes momento y rigidez, esta última debida a cambio de forma (I) o de material (E).

Como idea del valor aproximado de esta suma podemos tomar constantes E e I. El momento, como depende de la distancia, lo tomamos constante con distancia intermedia: con la mitad sale:

a = F L² / 2 E I

Inversamente, conocido el ángulo medio (promediado) flexado por el arco, podemos conocer aproximadamente la fuerza necesaria para ese flexado. Despejando:

F = 2 a E I / L²

Esa expresión nos permite calcular la flexión de barras no uniformes en sección (forma, anchura y espesor) o/y material (anisótropas). Véalo en Laminas multicapa. Se aplica todo en Pala_un diseño, y ya en unn modelo de arco, en Un modelo de arco mas detallado.

Una primera consecuencia, que se opone a una idea inmediata sobre los arcos, es que

cuanto más corto es el arco, más fuerza necesita para flexar.

En realidad muchos materiales, como los fibrosos naturales (madera) o artificiales (carbono, vidrio) tienen propiedades elásticas muy distintas según la dirección o eje de flexado. De modo que modernamente se citan las propiedades elásticas en forma de matriz de dimensión 3, una por cada eje coordenado. Los coeficientes en la diagonal principal son los módulos de Young en cada uno de los ejes, o sea, E_x, E_y y . E_z.. Los demás componentes tienen que ver con la torsión y el módulo de Poisson. No entramos por el momento a hablar de ellos mientras no nos sea necesario en este dominio de la arquería. También se usan las matrices de flexibilidad, de coeficientes inversos a E en la diagonal principal. En las demás componentes la relación es más complicada.

Por otra parte hay que recordar que la flexión tienen un límite de elasticidad, que varía para cada material, y que además ya no es igual para tracción y compresión, aunque el módulo sí lo sea. En toda flexión hay que comprobar por lo tanto que no se sobrepasan esos límites para que la pieza recobre su forma original. Ello nos sugiere además colocar materiales más resistentes a la compresión en la cara interna y más a extensión en la externa. Ello nos conduce inmediatamente a las Laminas multicapa..

Vuelta al Principio Última actualización: Thursday, 21 de February de 2013 Visitantes: