Esta página está en construcción: perdonen los errores y temas inacabados.

This page is being developed: I am sorry for errors and unfinished subjects.

 

Elasticidad y tracción (forma parte de Arqueria) 

Toda la historia de la mecánica de vigas (puentes, edificios, construcción en general) y vibraciones (en los mismos entornos y además en la música) tiene su origen en la elasticidad de los materiales con que construyen las cosas citadas.

Un material es elástico cuando, tras cambiar su forma bajo la acción de una fuerza, la recupera al cesar esa fuerza. Así lo hacen el acero, la madera, el cristal (siempre que antes no rompan si la fuerza es excesiva, claro). Y no lo hacen el chicle, el plomo, la plastilina. Estos ,materiales se llaman plásticos. En realidad esa elasticidad se mide con una variable que es grande para materiales elásticos y pequeña para plásticos. Se define como:

el alargamiento X que sufre la unidad de longitud
al aplicarle una tensión unidad (fuerza unidad sobre sección unidad)

o, en fórmula:

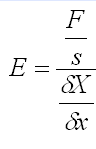
 (hay que especificar pues esas unidades o el sistema de medida), y se le llama el módulo de elasticidad, módulo elástico, módulo de Young, módulo de Hooke, con símbolo E frecuentemente, o Q.

Nótese que cuanto mayor es E mayor fuerza hay que ejercer para alargar una barra o hilo de longitud y sección determinadas. De modo que E es un índice de la resistencia al alargamiento por tracción, a la compresión y a la flexión. Mide pues la rigidez o cualidad similar. Pero reservamos el nombre de rigidez J a la resistencia a flexionar de una pieza de sección determinada (producto EI, siendo I el momento de inercia de la sección): así se hace en Elasticidad y flexión. y Laminas multicapa

Unidades

Véalas aquí: Unidades físicas

Algunos valores de E (tomadas de Olson, pg.14) para materiales comunes son (maderas en sentido de la fibra) (usamos el punto para marcar decimales y la coma para separar los miles, al estilo anglosajón. Perdón):

Metal  E  (din/cm2)
Tungsteno     35.0 .1011 
Níquel     21.0 .1011 
Acero     20.0 .1011 
Aluminio .     0.7 .1011
Plomo .     1.7 .1011
Madera  E  (din/cm2)
Fresno, Arce     1.3 .1011 
Nogal, Roble     1.2 .1011 
Olmo, Abeto     1.1 .1011 
Haya, Olmo     1.0 .1011 
Pino .   0.6 .1011
Material  E  (din/cm2)
Goma dura     2.3 .1010 
Goma blanda     0.5 .108 
Marfil     9.0 .1010 
Piel oveja     2.0 .109 
Shellac .   3.8 .1010

Timoshenko (p.5) ofrece sus datos

Metal  E  (Kg/cm2)
Acero al C  0.25%      2,000,000 
Acero al Ni  3.0 %      2,000,000
Cobre     1,100,000
Duraluminio .      700000  
Otros  E  (Kg/cm2) !
Madera     100,000 
Vidrio     700,000 
Hormigón (compr)      280,000 

Morley (p.89 y v 657) ofrece los suyos

Metal  E  (Kg/mm2)
Acero      20500 - 22000 
Hierro dulce     19000 - 20500 
Cobre       9500 - 11000
Bronce cañón .      8000 - 9500
Latón        8000 - 9500
Aluminio .      6300 - 8000  
Madera  E  (Kg/cm2) !
Fresno,     112000 
Roble inglés     104000 
Olmo       80000 
Abeto     112000 
Pino rojo .   112000
Teca     160000

Miravete y colaboradores ofrecen (p.5) a su vez, para nuevos materiales entre ellos fibras de carbono (unidades Gpa: como da 360 para tungsteno, y 198 para acero, debe ser algo así como centenas de Kg (fuerza) por milímetro cuadrado: en efecto, 2,050,000 Kg/mm2  equivale  a 2,050,000 Kg/(100 mm2)) =20500 Kg/mm2, valor próximo a 198 Gpa) de modo que aceptamos:                                                               Gpa <> 100 Kg/mm2:

o sea

 1 Gpa = 1 Kg-fuerza/décima de milímetro cuadrada.

Por su parte estas unidades admiten múltiplos y submúltuplos, al modo de los hertzios o vatios:.

 1 Gpa = 1000 Mpa         1 Mpa = 1000 Kpa         y así.

Fibras
  E  (Gpa)
Kevlar 29     65
Kevlar 40     125
Kevlar 140     185 
Vidrio E     75
Vidrio S     90
Boro     415
SiC     400
Fibra carbono
alquitrán
  E  (Gpa)
Amoco P-25     160
Amoco P-25     725
Nippon NT-20     200 
Nippon NT-60     595
Fibra carbono
poli...nitrilo
  E  (Gpa )
T-300     235
T-1000     295
GY-70     520 
AS-4     235
M-60J .   585
Resinas
  E  (Gpa )
Epoxi     3.7
T-1000     295
GY-70     520 
AS-4     235
M-60J .   585

Y Mercier, I, p 14.

Metal  E  (Kg/mm2)
 Cobre        10000
 Acero        20000 
 Aluminio .        7000
 Plomo          1700
 Estaño          5000
 Níquel        22000
Material  E  (Kg/mm2)
Madera 500
Vidrio  7500

Hay que unificar los datos para el sistema cegesimal (gramo-centímetro-segundo): por ejemplo el acero, que figura (en Mercier, pag.14) con E = 2.00 x 104 kg/mm2, lo pasamos (con cuidado)  al sistema CGS::

20000 Kg-fuerza/mm2
   = (2.00 x 104 kg-fuerza/mm2)  x (1000 gr-f / kg-f)  x  (100 mm2/cm2) (dyna  .  9.8.102cm/s2  / gr.fuerza) = 2 x 9.8 x 10 (4+3+2+2) =
= 19.6 .1011  dyn /cm2    

o sea, aproximadamente (tomamos 9.8 como 10) multiplicamos los Kg/mm2 por 100 millones, 108 , para obtener dyn/cm2 ;  y por 100, 102, para obtener Kg/cm2 ;  y dividimos por 100, multiplicamos por 10 -2, para obtener Gpa.

Comparemos materiales diversos, resumiendo las tablas anteriores, y ordenando de mayor E a menor. Añadimos sus densidades.

Material  E  (Kg/mm2)  d  (Kg/dm3)
 Amoco P-25      72500 1.9
 GY-70      52000  1.96
 Boro      41500 2.255
 T-1000      29500 1.82
 Acero      21000  8
 Kevlar 49      12500 1.44
 Cobre      10000  
 Vidrio E        7500 2.58
 Aluminio .      7000    
 Hormigón(RA)        2100  
 Fresno        1300 .87
 Pino        1000-600 0.5

El progreso traído por las fibras es incontestable, siendo además muy ligeras frente a los metales.

Un caso:  Para dejarlo muy claro: si colgamos un peso de un kilo de una barra de acero de 1 metro de largo y 1 centímetro cuadrado de sección,  ¿cuánto se nos alargará?. Despejando de la primera fórmula (y despreciando el peso de la propia barra):

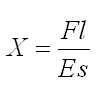
Veamos:

E = (1000 gr.peso / 1 cm2 ) (alarg / 100 cm) = 100000 / alarg.      alarg =100000 / ( 20.00 .1011  ) =20 .10-6 cm

 o sea, poquísimo, Colguemos 100 kilos y ahora ya: el alargamiento es 2 .10-3 cm, 2 milésimas de cm, 2 centésimas de milímetro. Muy poco todavía. Si colgamos mucho más corremos el riesgo de romper la barra, que tiene un límite de elasticidad o de rotura.

Otro caso ¿cuánto de deforma una barra de acero de 1 mm2 de sección y un metro de largo al colgarle 20 Kg.

Como E del acero es 20000 Kg/mm2, el alargamiento=20.1000/20000.1 = 1 mm. verosímil. Si colgamos pesos doble, cuádruple, etc. se nos duplicará cada vez ese alargamiento. ¿Hasta cuando? Hasta que se rompa. Algo antes, no obstante, puede llegarse a una alargamiento que ya no siga la ley de Hooke (proporcionalidad entre F y delta) o de elasticidad, que ya no recupere el tamaño inicial al retirar la fuerza.

¿y si es una cuerda de Kevlar de 1.80 metros?

Como E (Kevlar 125) es 12500 Kg/mm2, el alargamiento=20.1800/12500.1 = 3 mm. verosímil. Es el caso, aproximadamente, de una cuerda de arco.

Fluencia y rotura

Ese comportamiento elástico de proporcionalidad de alargamiento (o acortamiento) proporcional a esfuerzo y recobre total del tamaño primitivo sólo ocurre en un cierto margen de esfuerzos, margen que depende del material.

Todos los materiales rompen para una cierta carga de rotura, que expresamos también como Fuerza por unidad de área, por ejemplo, en Kg-fuerza/ mm2.

Y antes de ese valor hay en algunos materiales, como el acero un límite de furncia, en el que sin romper, se abandona el comportamiento proporcional que expresa la ley de Hooke

Movimientos  e inercia.

Lo anterior en cuanto a fuerzas y alargamientos. Pero al pensar en movimientos y vibraciones hay que contar con otra importante variable: la densidad del material, que ocasiona fuerzas de inercia frente a las que mueven el cuerpo. La fuerza motora es contrarrestada (en parte) por otra de inercia. Ya se comprende que cuanto mayor es la densidad del material, más despacio se mueve y por tanto vibra. (si lo duda, empuje un metro cúbico de paja primero y luego otro de acero. Escríbanos con sus impresiones, por favor).

 

Vea ahora la aplicación de todo esto a la flexión.

 

Vuelta al Principio    Última actualización: Thursday, 21 de February de 2013    Visitantes: contador de visitas