Láminas multicapa. I. Fibra neutra (forma parte de Arqueria)
Necesitamos conocer las cualidades elásticas de láminas compuestas por varias capas de diferente material para nuestra Pala. Y sabemos que necesitamos conocer el momento de inercia de la pala (variable en cada punto para una pala variable como la que pretendemos) .Ya vimos en Elasticidad y flexión la manera de calcular la capa neutra y el ángulo flexado por una barra para una sola capa homogénea.
Para varias capas hay que rehacer los cálculos en lugar de aplicar intuitivamente las fórmulas deducidas para una sola.
Capa neutra
Tenemos en general, como antes:
S d F = 0
Elijamos una referencia de alturas con origen en la capa neutra. Las alturas de las n capas son entonces:
a0 - a1 para la capa 1, a1 - a2 para la capa2,....an-1 - an para la capa n, la última.
La expresión queda, para cada capa
S d F = S (b dy )E y / R = (b E/ R) / S y dy = (b E/ 2R) (ai2- ai-12)
y para todas las capas
S i (Sy d F) = S i (b Ei / 2R) (ai2- ai-12) = (b /2R) S i Ei (ai2- ai-12) = 0
por lo que
S i Ei (ai2- ai-12) = 0
Esta ecuación relaciona las alturas de las capas y sus módulos de Young; la podemos incluso expresar como:
S i Ei (ai+ ai-1) (ai- ai-1) = 0 o bien
S i Ei .ami hi = 0
que nos expresa que
la suma de los productos del módulo, espesor y altura media para cada capa es nula cuando tomamos como referencia de alturas la capa neutra.Dos capas
Veamos el caso de dos capas, como el que se presenta en la figura; conocidos los módulos y los grosores de cada capa, tenemos entonces:
E1 h1 am1 +E2
h2 am2 = 0
es decir
am2 /am1 = - (E1 h1
/E2 h2 )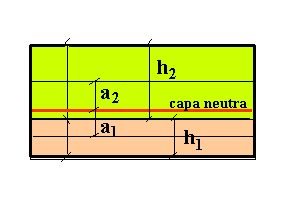
lo cual nos dice que las alturas medias están en relación inversa que los respectivos productos de modulo por espesor. Interpretando su significado tenemos que
0) los signos de ambas alturas son opuestos, al ser positivos siempre módulos y espesores; lo que implica que
1) la capa neutra está situada siempre entre ambas alturas medias de ambas capas; de hecho para una sola capa estaría en su altura media.
2) la capa neutra puede estar situada en cualquiera de las dos capas. Una parte de una de las capas trabaja a tracción y a compresión, la otra sólo a una de las maneras. ¿Cuándo está en el limite?.
3) si la de arriba, la 2ª, es mayor (es decir, la capa neutra se sitúa más abajo) ello es debido a la preponderancia del producto para la primera, E1 h1, la cual preponderancia es debida, o a la de su módulo, o a la de su espesor, o a la de ambos. Todo ello es lógico e intuitivo.
4) lo anterior nos dice a su vez que podemos compensar módulo alto con espesor bajo o viceversa.
5) lo anterior nos dice a su vez que podemos compensar módulo alto con espesor bajo o viceversa.
Tres capas en sándwich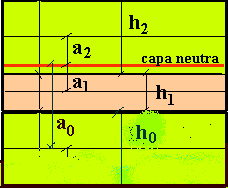
Tres capas de las que las dos extremas son iguales en módulo y espesor. Caso muy típico, por fácil y útil. La igualad y simetría de los parámetros y geometría nos dice ya que la la capa neutra coincide con la central o media de la capa central. Pero demostrémoslo por un prurito teórico.
Sea la capa cero una debajo de las dos en el caso anterior. Tenemos en este caso:
E2 h2 am0 + E1 h1 am1 + E2 h2 am2 = E2 h2 (am0 + am2 ) + E1 h1 am1 = 0 es decir
(am0 + am2 ) /am1 = - (E1 h1 /E2 h2 )
lo cual nos dice que
0) los signos de la altura media y la suma de las exteriores son opuestos.
1) Si am1 es positivo, la suma (am0 + am2 ) es negativa, lo que hace (am0 mayor en valor absoluto que am2.
2) . pero eso es imposible porque dando la vuelta a la lámina ( es decir, intercambiando los índices 0 y 2, tenemos la misma lámina y ahora será am0 menor en valor absoluto que am2.
3) . Si algo es mayor y menor que otra cas es que es igual, no puede darse la desigualdad. De modo que la suma es nula y lo mismo es ./am1: ello quiere decir que
4) la capa neutra pasa por la capa media de la capa central. Todo es sencillo.
Varias capas desiguales
La fórmula anterior
S i Ei .ami hi= 0
nos permite calcular su situación para cada caso de multicapa; en efecto si la distancia de la capa neutra a la base de la primera capa (dibujada abajo) es x, las alturas medias de cada capa pueden calcularse como la distancia a la base menos esa distancia x:
ami= dmi - x
pero esa distancia es igual a los espesores de todas las capas por debajo de ella, más la mitad del propio espesor:
dmi= hi / 2 + S j hj
así que
S i Ei .hi. ( dmi - x ) = S i Ei .hi. ( hi / 2 + S j hj - x ) = 0
así que
x = [ S i Ei .hi. ( hi / 2 + S j hj ) ] / [ S i Ei .hi ]
fórmula que nos permite, con toda generalidad, calcular la posición de la línea o superficie neutra en función únicamente de los módulos y espesores de cada capa.
Apliquémoslo al caso del sándwich visto antes, haciendo E0 = E2 = E y h0 = h2 = h (ver figura)
x = [ E .h ( h / 2 ) + E1 .h1 .( h1 / 2 + h ) + E .h .( h / 2 + h+ h1 ) ] / [ E .h + E1 .h1 + E .h ] =
= ( h +h1 /2) ( 2 E h + E1.h1 ) / ( 2 E h + E1 h1 ) = ( h +h1 /2)
que es precisamente la mitad del espesor del sándwich, como razonábamos antes.
En este estudio, así como en el de lámina homogénea, monocapa, se ha supuesto que el módulo de elasticidad a tracción y a compresión es el mismo para todos los materiales. No estará de más dudar sistemáticamente de este aserto en cada caso, comprobando en lo posible su pertinencia.
Pase a ver ahora II_Momentos y III.Fuerzas tangenciales y materiales.
Vuelta al Principio
Última
actualización:
Thursday, 21 de February de 2013 Visitantes: