Esta página está en construcción: perdonen los errores y temas inacabados.

This page is being developed: I am sorry for errors and unfinished subjects.

TXALAPARTA. Breve Estudio Acústico-Musical.

INTRODUCCIÓN

Con motivo de mi asistencia a la Txalaparta Festa de Hernani, amablemente invitado por Juan Mari Beltrán, organizador de la misma y profesor en la Musika Eskola del instrumento, me interesé por él, sobre todo tras oír los matices tímbricos y rítmicos que los txalapartaris asistentes produjeron a partir de tablones y barras de materiales diversos. El propósito de este escrito es contribuir al conocimiento de este instrumento vasco, desde le punto de vista físico-acústico, pero aplicándolo en lo posible a sus posibilidades musicales. Creemos que este breve estudio complementa otros varios, muy interesantes, cuyo punto de vista es más antropológico y etnomusicológico. Porque la txalaparta es más que una tabla, es verdad; pero también es una tabla, y como tal, ha de ser estudiada.

VIBRACIÓN TRANSVERSAL de TABLAS y BARRAS

Desde el punto de vista acústico, la txalaparta es una tabla o tablón que vibra sobre todo transversalmente, a flexión, cuando es golpeada por masas en esa dirección. Se pretende una suspensión tan flotante como sea posible para que la tabla vibre libremente; esa suspensión se logra generalmente mediante cestos de mimbre, balas de paja o maíz, etc.

Una tabla así golpeada, presenta vibraciones complejas, compuestas de varios parciales, vibraciones senoidales cuyas frecuencias no presentan relaciones numéricas sencillas (enteras) como lo hacen las cuerdas vibrantes o los tubos sonoros, ni siquiera aproximadamente. Esto hace que el timbre no sea tonal, o sea, la txalaparta no emite notas en general. No obstante, esos parciales están suficientemente separadas en frecuencia para que cada uno de ellos sea percibido aisladamente casi como nota independiente, con un cierto matiz de golpe con tono o casi tono.

Estos parciales corresponden a los modos de vibración que la geometría de la tabla permite, es decir, flexiones con una sola curvatura, con dos, con tres, etc.

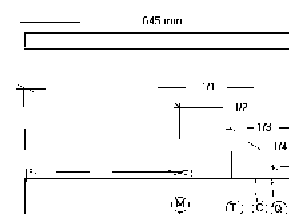
Numerando esos modos de vibrar parciales de acuerdo a ese número de curvaturas, tenemos los parciales, cuyos primeros cuatro representamos en la figura. Se observa que hay partes que en la vibración quedan inmóviles, mientras que otras presentan máximo desplazamiento transversal. Llamando a los primeros Nodos, y a los segundos Vientres, como en cuerdas y tubos, podemos conocer las frecuencias de esos parciales y la posición de los nudos mediante la fórmula y cuadro siguientes, tomados de [Olson,1957]:

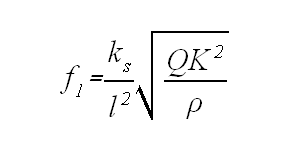
donde f es la frecuencias en hercios, o vibraciones por segundo,

ks es una constante que depende del modo de sujetar o apoyar la tabla o barra.

l es la longitud de la tabla, en centímetros

Q es el módulo de Young, en dynas por centímetro cuadrado, relacionado con la elasticidad del material a la flexión transversal.

K es el radio de giro, o punto donde , supuesta concentrada toda la masa, obtendríamos igual momento de inercia ( masa de giro podemos llamarla ). Depende de la forma de la sección de la tabla, rectangular por lo general.

r es la densidad del material, en gramos por centímetro cúbico.

Ahora bien, como se conocen los radios de giro para varias formas, rectangular, circular y tubular, y todas son proporcionales al grosor de la tabla en la dirección de flexión, en definitiva, la frecuencia depende,por un lado, de las dimensiones longitud y anchura ( l, a ), y, por el otro, de constantes que dependen del material ( r , Q ). Si sacamos fuera de la raíz el radio de giro K, que depende de la forma de la sección, y agrupamos en una sola constante las que dependen del material, en general:, donde las cuatro constantes dependen respectivamente del parcial considerado, del material, del tipo de sujeción, y de la forma de la sección.

f SUB 1 = k SUB p k SUB m k SUB s k SUB f TIMES {a OVER l SUP 2 }

La fórmula anterior proporciona las frecuencias de los primeros parciales de una barra dependiendo de su material, de su forma y del modo de sujetarla. Además, nos ofrece ya algunos interesantes comentarios para el txalapartari:

1. Los sonidos de la txalaparta no dependen de la anchura de ésta, sólo del grosor y de la longitud.

2. El sonido es más agudo ( mayor frecuencia ) cuanto menos longitud, más corta la tabla, lo que es y parece normal.

3. El sonido es más agudo cuanto más gruesa ( mayor a ) es la tabla, lo que a primera vista sorprende. Pero se entiende al recordar que cuanto más gruesa, más resistente es a la flexión, y la fuerza de recuperación es mayor.

Veamos ahora algunas tablas que nos permiten calcular las frecuencias deseadas.

SUJECIÓN	ks	k_p1	k_p2	k_p3	k_p4
empotrada 1	.561	1	6.26	15.55	34.39
1empot.1 suj o 1 sujeta	2.45	1	3.25	6.75	11.5
libre o 2 empot	3.56	1	2.756	5.404	9.933
2 sujeta	3.14	1	4	9	16

Para la tabla con sujeción libre, repetimos los valores relativos al primer parcial, con el intervalo aproximado que respecto a él tienen ( 8º y 4º son octava y cuarta justas, 3ºM es tercera mayor y q es un cuarto de tono) Se incluye además La situación de los nodos (puntos sin vibración ) y los vientres o antinodos (puntos de máxima vibración) son, para esos cuatro primeros parciales:

PARCIAL	k_p	intervalo	nodos	vientres (aprox)
1	1	0	.2242	.50
2	2.756	8º+4º+q	.1321 .50	.316
3	5.404	2.8º+4º	.0944 .3558	.2251
4	9.933	3.8º+3ºM	.0734 .2770 .50	.1552 .3885

de modo que golpear en un nodo es evitar el parcial correspondiente, mientras que golpear en un vientre, es hacerlo sonar con toda su amplitud. Todo golpe, pues pondrá en movimiento cada uno de los parciales con amplitudes dependientes de la posición de sus nudos y vientres: cada punto proporciona una combinación de parciales única, un espectro: es decir, un timbre determinado.

Algunos puntos, no obstante, merecen especial atención:

El centro, C, que hace sonar máximamente p1 y p3, mientras que p2 y p4 quedan omitidos.

El cuarto Q, cerca del nodo 1, a .22 del extremo, que hace sonar p3 especialmente, suprimiendo p1, y haciendo sonar algo p2 y p4.

El tercio T, que hace sonar especialmente p2, mientras que p1, p3 y p4 suenan poco.

El Sexto, S, que hace sonar especialmente el cuarto, p4, mientras que p2, p1 y p3 son pequeños.

De modo que podemos individualizar cada uno de cuatro primeros armónicos golpeando respectivamente en C, T, Q, y S.

Los radios de giro, para diversas formas de la sección:

SECCIÓN	k_f	a
rectangular	.29	grosor,
circular (barra)	.25	diámetro, D
anillo (tubo)	.5	raíz ( D² + d²)

y los materiales:

MADERA	k_m
fresno	450693
haya	392232
corcho	49799
olmo	430331
abeto	464420
caoba	405190
arce	437237
roble blanco	408248
pino blanco	365148
álamo blanco	466252
sicomoro	430331
nogal	462910

METAL	k_m Transversales y Longitudinal	k_m' Torsión.
acero	365000	8649
fundición	463000	7247
latón		7162

En particular nos interesan aquí los modos de vibración de la txalaparta de madera, rectangular, y los de la tobera, metálica, rectangular o redonda, ambas vibrando libremente o casi. Por ejemplo,

TXALAPARTA de NOGAL:

Se considera tablón rectangular, sujeción libre, f1 = ( 1 x 3.56 x 462910 x .29) x a / l² , o sea,

f1 = 477908 . a / l²

De modo que una tabla de 2 metros ( 200 cm) de larga y 4 centímetros de gruesa, dará un fundamental (parcial 1) de 47.8 hercios, muy grave, aproximadamente un SOL1, tecla 11 del piano.

Si se acorta la tabla a la mitad, la frecuencia queda multiplicada por 4 ( la longitud está elevada la cuadrado ), o sea f1 = 191.161 hercios, SOL3 (algo bajo), tecla 35 del piano.

TABLA de PINO.

Una tabla de pino cuyas dimensiones son: 101.8 x 11.8 x 2.3--2.5 cm ha sido golpeada para comprobar la fórmula anterior. Las frecuencias teóricas del primer parcial, y los tres siguientes, son:

f1 = ( 1 x 3.56 x 365148 x .29) x 2.4 / 102.8² = 87.30 para a=2.4

f2 = f1 x 2.75 = 240.6 f3= f1 x 5.404 = 471.79 f4= f1 x 9.933 = 867.19

Analizados los parciales realmente emitidos, se obtuvieron los siguientes resultados:

PARCIAL	frecuen. teórica (hz)	frecuencia real (hz)	desviación:6 % = 1 sem
1	87.3	92.25	+6%
2	240.6	240	-0.6 %
3	471.79	472.5	+0.1%
4	867	885	+2%

Dada la imprecisión en el conocimiento del grano de la madera, y en el grosor del tablón, consideramos los resultados suficientemente exactos.

ANCHURA de la TABLA

Hemos visto que la anchura de la tabla (dirección perpendicular a la de flexión) no influye teóricamente en las frecuencias emitidas; pero otra cosa es la radiación al exterior de esas frecuencias. Para esto sí hace falta una cierta superficie, sobre todo para radiar las más graves, al igual que ocurre en los altavoces e instrumentos graves que son grandes. Creemos pues que hacen falta tablas anchas para que los parciales graves cobren importancia, se oigan: de lo contrario se desaprovechan las posibilidades de una txalaparta grande, porque sus frecuencias graves, presentes, no son radiadas al exterior, no se oyen..

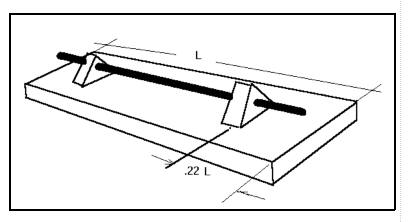
Algo similar ocurre en las barras metálicas. Una posibilidad de hacer audibles las bajas frecuencias consiste en trasmitirlas a una tabla ancha y hacer que ésta las radie al exterior. Se trata de una tabla armónica, como la del piano, o violín. Para ello hay que fijar de alguna manera la barra a la tabla, y esto obligaría a suprimir algún modo libre. Lo lógico es fijar la tabla por loa nodos del fundamental, hacia un quinto de su longitud. por ambos extremos, por medio de un puente que sujeta, no basta apoyar. Si se elige además una tabla con modos de vibración similares (igual longitud), las bajas frecuencias de la barra serán amplificadas por la tabla, radiando muy eficientemente. Experimentos efectuados por nosotros muestran que en efecto, así sucede, oyéndose bellos graves.

VIBRACIONES TRANSVERSALES COMPUESTAS.

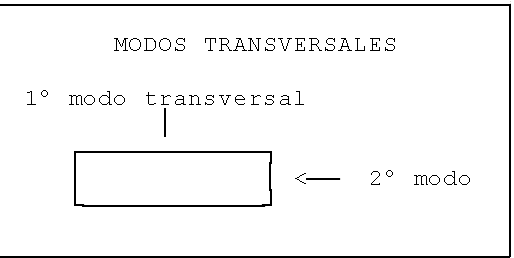
En lo anterior hemos considerado una vibración transversal, para la que contaban longitud y grosor, pero no anchura. Ahora bien, la tabla también puede vibrar perpendicularmente a la dirección anterior: lo que era anchura es ahora grosor, y lo que era grosor es ahora anchura. A poco que se golpee sesgadamente la tabla en una de sus caras, se pondrán en movimiento los dos tipos de vibración transversal que comentamos. Ahora sí que tiene interés la otra dimensión. Una juiciosa elección de ambas dimensiones ( cualquier proporción sencilla, como 2:1, 3:1, 3:2...) puede conseguir timbres que podemos calificar de "diseño". En todo caso, se busque o no ese efecto, estará presente, y ambos modos de vibración se darán en la txalaparta real.

Hay que hacer notar que la constante del material, km no será idéntica, pues depende de la elasticidad, que varía según la relación del corte a la fibra, en los materiales no homogéneos, como la madera.

Hay un tercer modo de vibración para una tabla o barra: la longitudinal, en la que en lugar de flexionarse trasversalmente, sufre alternativas expansiones y compresiones, producidas por un golpe sobre el extremo, perpendicularmente a las otras dos direcciones anteriores. Se golpea en la dirección longitudinal, apareciendo entonces otra serie de parciales, ahora armónicos, que dependen sólo de la longitud y del material:

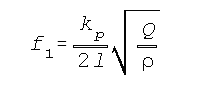
y, calculando como para las transversales, las constantes del material bajo raíz, queda:

siendo k''m la misma constante del material que antes, excepto que debido a la inhomogeneidad del material, por ejemplo en la madera, no será ya idéntico. Por su parte, kp se reduce ahora a la serie armónica 1, 2, 3,..etc.

La barra se comporta pues como una cuerda o tubo, salvo la diferente significación de k"m que depende en las cuerdas de la tensión y la densidad lineal.

Incluso, como todos los cuerpos, la tabla o barra puede torsionar, es decir, perder su carácter lano, y alabearse. Como experimenta una resistencia a ello, si es elástico, volverá a su posición de equilibrio, seguirá la torsión en sentido contrario, y así sucesivamente: vibrará.

Este modo de vibrar se excitará cuando se golpea en un punto lateral (ver figura, punto x) , tanto en sentido longitudinal, como se hace para la flexión normal, como transversal. apareciendo entonces otra serie de parciales, ahora armónicos, que dependen sólo de la longitud, de la densidad y de los módulos de Young, Q, y Poisson, s. Sus frecuencias son:

y pasando, como antes a calcular las cantidades bajo raíz, obtenemos otra constante del material, km', que figura, para algunos metales, en las tablas anteriores.

La barra se comporta pues, también, como una cuerda o tubo, salvo la diferente significación de k'm que depende en las cuerdas de la tensión y la densidad lineal, y en la torsión, de los módulos de Young y Poisson, y la densidad.

Se observa (dividiendo ambas fórmulas) que las frecuencias longitudinales y torsionales están en relación fija, relación que depende del material, del llamado módulo de Poisson; puede calcularse que esta relación es aproximadamente de cuarta (4:3) para el paladio, de tercera mayor (5:4), para el acero y hierro forjado, y de tercera menor estrecha (7:6) para el zinc.

Hemos visto cómo influencia el modo de sujetar la txalaparta a los parciales, y por ende, al timbre emitido. En principio es simple, como ocurre en las cuerdas: la inmovilización de la tabla en un nodo de un parcial (permitiendo su giro, claro está) no afecta a dicho parcial, pero sí a los que no tienen nodo, bien sea un vientre, supresión máxima, o lugar intermedio (supresión parcial). La vibración libre permite todos los parciales, pero es una situación ideal: el peso del instrumento tenderá a apretarlo contra el apoyo, por blando que sea; se intentan, como decíamos, apoyos que aproximen la sujeción a la libre.

Una posibilidad sería colgarla tabla de modo que su peso no apriete la tabla contra el apoyo en el sentido de su vibración transversal: ello se conseguiría colocándola vertical, con su anchura perpendicular al suelo. Se golpearía entonces horizontalmente (comprendemos el horror hacia este cambio en la Tradición), vibrando en esa dirección, mientras que el peso iría en vertical, sin inteferirse. La sujeción resultaría así libre, para la dirección de vibración.

Por último, puede emplearse musicalmente, durante la ejecución, la influencia de la sujeción en el timbre: colocando una mano en lugares específicos, incluso presionando más o menos, pasaremos de una sujeción a otra, modificando el sonido, el timbre de la txalaparta. Estos contactos momentáneos se realizan en tambores, variando tono junto con timbre, y en cuerdas (como en el salterio persa, o santur), para modificar tono-

No sólo influye en el timbre emitido por la tabla el lugar de golpeo, como se ha visto. También la forma de golpear influye. Naturalmente, cuanto más fuertemente se golpea, más fuerte es el sonido. Pero además, esa fuerza, más repentina, más veloz, crea una deformación más brusca en el punto de impacto, originando flexiones de más arista, podemos decir, lo que corresponde a parciales más agudos: como ocurre en la cuerda, la forma de onda creada al pulsar, da lugar a un reparto armónico más o menos desplazado hacia el agudo.

Por igual razón, un palo fino producirá deformaciones más agudas y parciales más agudos, mientras que un palo ancho y redondeado, pondrá en juego parciales más graves.

Los palos que golpean la tabla son golpeados asimismo por ella: es un choque en el que todos reciben un golpe. Por lo tanto los palos suenan, y ese sonido pertenece al sonido total de la txalaparta. Como tales barras percutidas longitudinalmente, emitirán parciales que como veremos más adelante son frecuencias armónicas. Aquí también influirá el lugar de sujeción: se potenciaran las frecuencias con nodos en ese lugar, a costa de los que tienen un vientre.

Según la dirección, lugar y modo de golpear la tabla o barra encontraremos una combinación única de modos de vibración y de parciales que hacen cada golpe irrepetible; esto sin descender al detalle, permite acercarse al hecho sorprendente de que un instrumento tan aparentemente simple, interese: incluso olvidando la rítmica y la dinámica del toque de la txalaparta, tenemos una tímbrica muy rica, a cuyos fundamentos físicos hemos querido acercarnos en este breve estudio.

Las consideraciones anteriores podrán, esperamos, junto a la comprensión del instrumento, sugerir a los txalapartaris nuevos modos de construirlo y tocarlo, es decir, a desarrollar este interesante instrumento vasco, para cuyo conocimiento y desarrollo esperamos sea útil el presente escrito.

BELTRAN, J.M. "Txalaparta". Cuad.Etnol.Etnog.Navarra. nº52. pp.419-439. Jul-Dic, 1988.

TIMOSHENKO, S. Vibration problems in Engineering.Van Nostrand. New York, 1929. pp.290