Fuerzas longitudinales (forma parte de Arqueria)
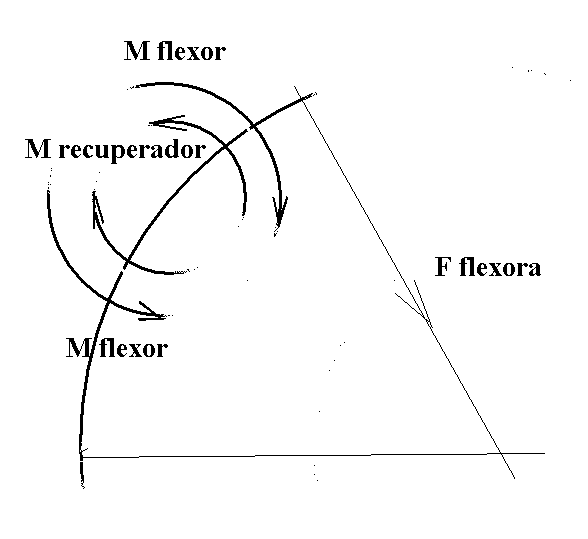
Veíamos las fuerzas normales, flectoras, en Un modelo de arco mas detallado. Hasta ahora henos despreciado las componentes paralelas a cada tramo.
Contamos con dos tipos de fuerzas que, aunque suelen despreciarse en cálculos básicos, podemos tomar en consideración para comprobar su influencia. Son de dos tipos:
Fuerzas de compresión-expansión Fuerzas de cortadura
Las primeras deben ser estudiadas con cuidado porque modifican la teoría simple de la flexión y desplazan la capa neutra del su posición cuando no aparecen.
Su expresión es:
******
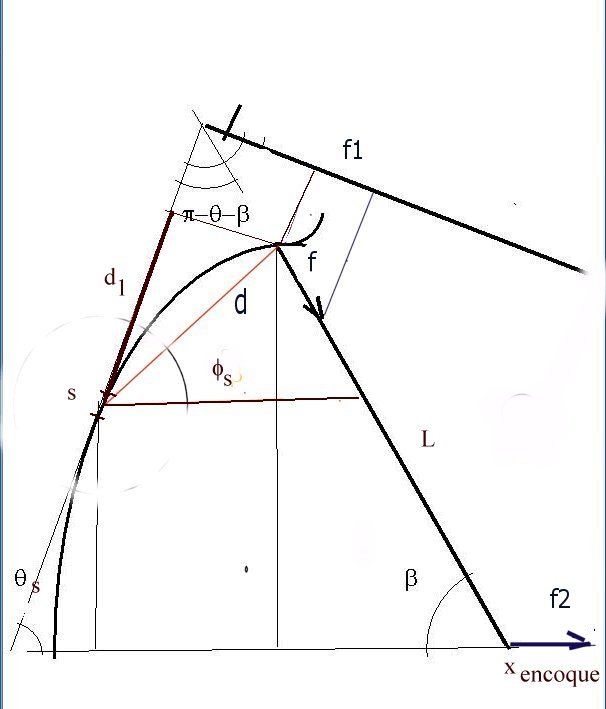
El momento flector de la fuerza F respecto al elemento de arco s es igual al producto de la componente de la fuerza normal a s multiplicado por sus distancia a s.. La componente de la fuerza es f1, y la distancia es f1, cuyos valores respectivos son:
f1 = f . sin ( b+fs ) d1 = d . cos ( qs-fs )
Los paréntesis son ángulos limitados superiormente: el primero,( b+fs ,está limitado entre p
, para tensión pequeña, aunque siempre el arco curvado a la derecha; y p / 2, para gran tensión; incluso menor exagerando ésta. Por lo tanto el seno de ese ángulo está a su vea limitado entre 0 y 1 aproximadamente.
A su vez e segundo paréntesis, qs-fs , vale entre 0, para poca tensión, y hasta .p / 2, aproximadamente, para puntos de mucha curvatura; por ello el coseno de ese ángulo vale entre 1 y .7. El producto amabas funciones vale pues entre 0 y .7.
El momento flector
M = f1 . d1
y como contamos con la expresión general del ángulo de flexión en el elemento de arco de longitud s:
as = Ms/EI
donde E es el módulo elasticidad de Hooke, ligada a al rigidez o fortaleza del arco, y donde I, momento de inercia de una sección recta de anchra a y grosor b es:
I = a.b^3/12
con lo que tenemos:
as = /12/E ) . f1 . d1 / (a.b^3)
En cuanto a la fuerza f2 que ejerce brazo-mano-dedos sobre la cuerda, vale evidentemente:
f2 = f . cos (b )
Así que podemos calcular el conjuntos de puntos de la función f2 = f2 ( x2 ), Fuerza efectuada sobre la cuerda. en relación con la distancia de encoque al apoyo en el arco, función que acaba cuando esa distancia alcanza la longitud de la flecha. Esa función es evidentemente creciente, mínima pra el arco sin tensar y máxima para la distancia igual a la flecha.
Podemos encontrar empíricamente la función para cada arco, colgando el arco por su centro y colgando pesos crecientes del punto de la cuerda donde lse inserta la flecha, midiendo los pares de valores Peso colgado-distancia. Así se hace en Energía almacenada en arco.
Vuelta al Principio
Última
actualización:
Thursday, 21 de February de 2013
Visitantes: