Esta página está en construcción: perdonen los errores, repeticiones y temas inacabados.

 

This page is being developed: I am sorry for errors, duplications  and unfinished subjects.

 

 

Ángulos de los huesos VI  (incluido en Danzante)

 

Tras publicar en  Ángulos de los huesos I, II y III  IV y V, añadimos lo que hemos aprendiendo acá y acullá sobre matrices y cuaterniones. Ya hemos trabajado en Matrices en espacio vectorial 3D.

 

Por un lado, los cuaterniones están normalizados cuando su 'módulo'  raiz cuuadrada de suma de las CUATRO cooedendas en 1. Además la as coordenadas i,j,k representan la direccion del eje en el espacio (tres cosenos de los nahilos del eje co las tres direcciones x,y,z. Y la cuarta, w es el coseno de la mitad del ánguklo que se gira (luego está entre 0 y 90,.

 

Un ejemplo de esos datos se lista a continuación. (recordemos que todavía se lista el arco coseno de Quaternion.w y no el doble, angulo de giro

 

Informaciones |------------------------------------------------------------- |------------------------------------------------------------- Microsoft.Kinect.BoneOrientationCollection del cuadro: 291 |------------------------------------------------------------- |------------------------------------------------------------- | Hues: 3. Long (espacial, normal): 019 | 014 cm.  Arti: de ShoulderCenter:2 a Head:3 | Posi: de 014 -024 240 a 022 -008 243 cm |Rotaciones Absolutas Microsoft.Kinect.Vector4 | Cuat: ,225 ,855 -,037 ,465 | ángu: 062 077 031 092 grados | Matr, valores y ángulos: Microsoft.Kinect.Matrix4 | -,466 ,350 -,812 ,000 | 118 069 144 090 | ,420 ,896 ,145 ,000 | 065 026 082 090 | ,779 -,273 -,565 ,000 | 039 106 124 090 | ,000 ,000 ,000 1,000 | 090 090 090 000 grados Compr modulos hori y verti y quat:1,000 1,000 1,000 |Rotaciones Jerárquicas | Cuat: ,126 -,030 ,230 ,965 | áng: 015 083 092 077 grados | Matr, valores y ángulos: | ,893 ,435 ,115 ,000 | 027 064 083 090 | -,450 ,863 ,229 ,000 | 117 030 077 090 | ,000 -,256 ,967 ,000 | 090 105 015 090 | ,000 ,000 ,000 1,000 | 090 090 090 000 grados Compr modulos hori y verti y quat:1,000 1,000 1,000 | |------------------------------------------------------------- | Hues: 4. Long (espacial, normal): 017 | 012 cm. | Arti: de ShoulderCenter:2 a ShoulderLeft:4 | Posi: de 014 -024 240 a 005 -034 229 cm |Rotaciones Absolutas Microsoft.Kinect.Vector4 | Cuat: ,784 -,434 ,393 -,206 | ángu: 102 038 116 067 grados | Matr, valores y ángulos: Microsoft.Kinect.Matrix4 | ,314 -,842 ,438 ,000 | 072 147 064 090 | -,519 -,538 -,664 ,000 | 121 123 132 090 | ,795 -,019 -,606 ,000 | 037 091 127 090 | ,000 ,000 ,000 1,000 | 090 090 090 000 grados Compr modulos hori y verti y quat:1,000 1,000 1,000 |Rotaciones Jerárquicas  Cuat: ,000 ,000 -,854 ,520 | áng: 059 090 090 149 grados | Matr, valores y ángulos: | -,460 -,888 ,000 ,000 | 117 153 090 090 | ,888 -,460 ,000 ,000 | 027 117 090 090 | ,000 ,000 1,000 ,000 | 090 090 000 090 | ,000 ,000 ,000 1,000 | 090 090 090 000 grados Compr modulos hori y verti y quat:1,000 1,000 1,000 | |------------------------------------------------------------- | Hues: 5. Long (espacial, normal): 024 | 016 cm. | Arti: de ShoulderLeft:4 a ElbowLeft:5 | Posi: de 005 -034 229 a -010 -030 211 cm |Rotaciones Absolutas Microsoft.Kinect.Vector4 | Cuat: -,589 ,691 -,282 ,311 | ángu: 072 126 046 106 grados | Matr, valores y ángulos: Microsoft.Kinect.Matrix4 | -,113 -,989 -,097 ,000 | 097 171 096 090 | -,638 ,147 -,756 ,000 | 130 082 139 090 | ,762 -,024 -,647 ,000 | 040 091 130 090 | ,000 ,000 ,000 1,000 | 090 090 090 000 grados Compr modulos hori y verti y quat:1,000 1,000 1,000 |Rotaciones Jerárquicas | Cuat: -,026 -,003 ,350 ,936 | áng: 021 092 090 070 grados | Matr, valores y ángulos: | ,755 ,656 -,012 ,000 | 041 049 091 090 | -,655 ,754 -,051 ,000 | 131 041 093 090 | -,024 ,047 ,999 ,000 | 091 087 003 090 | ,000 ,000 ,000 1,000 | 090 090 090 000 grados Compr modulos hori y verti y quat:1,000 1,000 1,000 |------------------------------------------------------------- | Hues: 6. Long (espacial, normal): 028 | 017 cm. | Arti: de ElbowLeft:5 a WristLeft:6 | Posi: de -010 -030 211 a -023 -023 187 cm |Rotaciones Absolutas Microsoft.Kinect.Vector4 | Cuat: -,511 ,694 -,324 ,390 | ángu: 067 121 046 109 grados | Matr, valores y ángulos: Microsoft.Kinect.Matrix4 | -,175 -,962 -,210 ,000 | 100 164 102 090 | -,457 ,268 -,848 ,000 | 117 074 148 090 | ,872 -,052 -,486 ,000 | 029 093 119 090 | ,000 ,000 ,000 1,000 | 090 090 090 000 grados Compr modulos hori y verti y quat:1,000 1,000 1,000 |Rotaciones Jerárquicas | Cuat: ,098 -,006 ,065 ,993 | áng: 007 084 090 086 grados | Matr, valores y ángulos: | ,991 ,128 ,026 ,000 | 008 083 089 090 | -,131 ,972 ,194 ,000 | 098 014 079 090 | ,000 -,196 ,981 ,000 | 090 101 011 090 | ,000 ,000 ,000 1,000 | 090 090 090 000 grados Compr modulos hori y verti y quat:1,000 1,000 1,000 |------------------------------------------------------------- | Hues: 7. Long (espacial, normal): 012 | 007 cm. | Arti: de WristLeft:6 a HandLeft:7 | Posi: de -023 -023 187 a -028 -017 177 cm |Rotaciones Absolutas Microsoft.Kinect.Vector4 | Cuat: -,445 ,745 -,275 ,414 | ángu: 066 116 042 106 grados | Matr, valores y ángulos: Microsoft.Kinect.Matrix4 | -,261 -,890 -,373 ,000 | 105 153 112 090 | -,435 ,454 -,778 ,000 | 116 063 141 090 | ,862 -,041 -,506 ,000 | 030 092 120 090 | ,000 ,000 ,000 1,000 | 090 090 090 000 grados Compr modulos hori y verti y quat:1,000 1,000 1,000 |Rotaciones Jerárquicas | Cuat: -,012 -,001 ,099 ,995 | áng: 006 091 090 084 grados | Matr, valores y ángulos: | ,980 ,197 ,000 ,000 | 011 079 090 090 | -,197 ,980 -,025 ,000 | 101 011 091 090 | -,005 ,024 1,000 ,000 | 090 089 001 090 | ,000 ,000 ,000 1,000 | 090 090 090 000 grados Compr modulos hori y verti y quat:1,000 1,000 1,000 ...

 

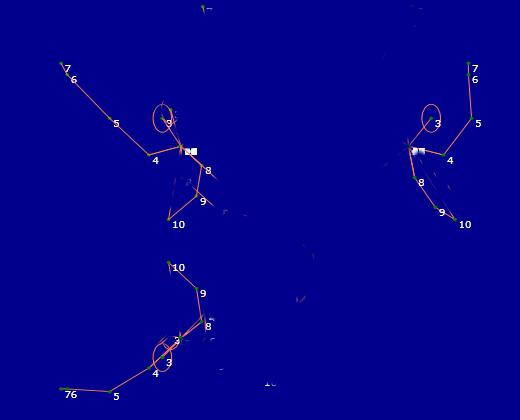
Añadimos más tarde los valores del eje y ángulo de los cuaterniones (absoluto y jerárquico) de cada hueso .  La posición del esqueleto correspondiente puede verse en la figura. Para conseguir esos valores hemos pasado de los cuaterniones Kinect (definidos en la librería s Microsoft.Kinect, a los cuaterniones definidos en System.Windows.Media.Media3D. Son similares pero incompatibles en cuanto a las operaciones y propiedades. Estos valores de eje y ángulo de esos cuaterniones nos aclaran su función para definir las orientaciones de los huesos.

 

Informaciones
|-------------------------------------------------------------
|-------------------------------------------------------------
Microsoft.Kinect.BoneOrientationCollection del cuadro: 232
|-------------------------------------------------------------
|-------------------------------------------------------------
| Hues: 3. Long (espacial, normal): 017 | 014 cm.
| Arti: de ShoulderCenter:2 a Head:3 | Posi: de 029 -027 271 a 025 -010 269 cm
|Rotaciones Absolutas
Microsoft.Kinect.Vector4
| Cuat: -,087 ,904 -,083 -,410 | ángu: 114 095 025 095 grados Eje:- ,095 ,991- ,091 Ángulo: 228 º
| Matr, valores y ángulos:
Microsoft.Kinect.Matrix4
| -,648 -,089 ,756 ,000 | 130 095 041 090
| -,225 ,971 -,079 ,000 | 103 014 095 090
| -,727 -,221 -,650 ,000 | 137 103 131 090
| ,000 ,000 ,000 1,000 | 090 090 090 000 grados
Compr modulos hori y verti y quat:1,000 1,000 1,000
|Rotaciones Jerárquicas
| Cuat: ,087 ,011 -,128 ,988 | áng: 009 085 089 097 grados Eje: ,559 ,072- ,826 Ángulo: 18 º
| Matr, valores y ángulos:
| ,967 -,251 -,044 ,000 | 015 105 093 090
| ,255 ,952 ,168 ,000 | 075 018 080 090
| ,000 -,174 ,985 ,000 | 090 100 010 090
| ,000 ,000 ,000 1,000 | 090 090 090 000 grados
Compr modulos hori y verti y quat:1,000 1,000 1,000
|
|-------------------------------------------------------------
| Hues: 4. Long (espacial, normal): 019 | 016 cm.
| Arti: de ShoulderCenter:2 a ShoulderLeft:4 | Posi: de 029 -027 271 a 016 -031 284 cm
|Rotaciones Absolutas
Microsoft.Kinect.Vector4
| Cuat: ,721 -,568 -,293 ,266 | ángu: 075 044 125 107 grados Eje: ,748- ,589- ,304 Ángulo: 149 º
| Matr, valores y ángulos:
Microsoft.Kinect.Matrix4
| ,182 -,976 -,121 ,000 | 079 167 097 090
| -,664 -,213 ,717 ,000 | 132 102 044 090
| -,725 -,050 -,687 ,000 | 136 093 133 090
| ,000 ,000 ,000 1,000 | 090 090 090 000 grados
Compr modulos hori y verti y quat:1,000 1,000 1,000
|Rotaciones Jerárquicas
| Cuat: ,000 ,000 -,827 ,562 | áng: 056 090 090 146 grados Eje: ,000 ,000- 1,000 Ángulo: 112 º
| Matr, valores y ángulos:
| -,369 -,930 ,000 ,000 | 112 158 090 090
| ,930 -,369 ,000 ,000 | 022 112 090 090
| ,000 ,000 1,000 ,000 | 090 090 NeuN090
| ,000 ,000 ,000 1,000 | 090 090 090 000 grados
Compr modulos hori y verti y quat:1,000 1,000 1,000
|
|-------------------------------------------------------------
| Hues: 5. Long (espacial, normal): 025 | 022 cm.
| Arti: de ShoulderLeft:4 a ElbowLeft:5 | Posi: de 016 -031 284 a 001 -014 295 cm
|Rotaciones Absolutas
Microsoft.Kinect.Vector4
| Cuat: -,339 ,913 ,227 -,015 | ángu: 091 110 024 077 grados Eje:- ,339 ,913 ,227 Ángulo: 182 º
| Matr, valores y ángulos:
Microsoft.Kinect.Matrix4
| -,769 -,626 -,127 ,000 | 140 129 097 090
| -,612 ,667 ,425 ,000 | 128 048 065 090
| -,181 ,404 -,896 ,000 | 100 066 154 090
| ,000 ,000 ,000 1,000 | 090 090 090 000 grados
Compr modulos hori y verti y quat:1,000 1,000 1,000
|Rotaciones Jerárquicas
| Cuat: ,218 -,299 ,410 ,834 | áng: 033 077 107 066 grados Eje: ,395- ,541 ,743 Ángulo: 67 º
| Matr, valores y ángulos:
| ,486 ,553 ,677 ,000 | 061 056 047 090
| -,814 ,569 ,119 ,000 | 144 055 083 090
| -,319 -,608 ,727 ,000 | 109 127 043 090
| ,000 ,000 ,000 1,000 | 090 090 090 000 grados
Compr modulos hori y verti y quat:1,000 1,000 1,000
|
|-------------------------------------------------------------
| Hues: 6. Long (espacial, normal): 026 | 023 cm.
| Arti: de ElbowLeft:5 a WristLeft:6 | Posi: de 001 -014 295 a -015 006 293 cm
|Rotaciones Absolutas
Microsoft.Kinect.Vector4
| Cuat: -,333 ,941 ,000 ,067 | ángu: 086 109 020 090 grados Eje:- ,334 ,943 ,000 Ángulo: 172 º
| Matr, valores y ángulos:
Microsoft.Kinect.Matrix4
| -,769 -,626 -,127 ,000 | 140 129 097 090
| -,626 ,779 -,044 ,000 | 129 039 093 090
| ,126 ,045 -,991 ,000 | 083 087 172 090
| ,000 ,000 ,000 1,000 | 090 090 090 000 grados
Compr modulos hori y verti y quat:1,000 1,000 1,000
|Rotaciones Jerárquicas
| Cuat: ,241 ,000 ,000 ,970 | áng: 014 076 090 090 grados Eje: 1,000 ,000 ,000 Ángulo: 28 º
| Matr, valores y ángulos:
| 1,000 ,000 ,000 ,000 | NeuN090 090 090
| ,000 ,884 ,468 ,000 | 090 028 062 090
| ,000 -,468 ,884 ,000 | 090 118 028 090
| ,000 ,000 ,000 1,000 | 090 090 090 000 grados
Compr modulos hori y verti y quat:1,000 1,000 1,000
|
|-------------------------------------------------------------
| Hues: 7. Long (espacial, normal): 006 | 005 cm.
| Arti: de WristLeft:6 a HandLeft:7 | Posi: de -015 006 293 a -018 011 294 cm
|Rotaciones Absolutas
Microsoft.Kinect.Vector4
| Cuat: -,222 ,972 ,037 ,060 | ángu: 087 103 013 088 grados Eje:- ,223 ,974 ,037 Ángulo: 173 º
| Matr, valores y ángulos:
Microsoft.Kinect.Matrix4
| -,894 -,428 -,133 ,000 | 153 115 098 090
| -,437 ,898 ,045 ,000 | 116 026 087 090
| ,101 ,098 -,990 ,000 | 084 084 172 090
| ,000 ,000 ,000 1,000 | 090 090 090 000 grados
Compr modulos hori y verti y quat:1,000 1,000 1,000
|Rotaciones Jerárquicas
| Cuat: -,029 -,003 ,117 ,993 | áng: 007 092 090 083 grados Eje:- ,243- ,029 ,970 Ángulo: 14 º
| Matr, valores y ángulos:
| ,973 ,232 ,000 ,000 | 013 077 090 090
| -,232 ,971 -,059 ,000 | 103 014 093 090
| -,014 ,057 ,998 ,000 | 091 087 003 090
| ,000 ,000 ,000 1,000 | 090 090 090 000 grados
Compr modulos hori y verti y quat:1,000 1,000 1,000
|
|-------------------------------------------------------------
| Hues: 8. Long (espacial, normal): 014 | 012 cm.
| Arti: de ShoulderCenter:2 a ShoulderRight:8 | Posi: de 029 -027 271 a 037 -036 263 cm
|Rotaciones Absolutas
Microsoft.Kinect.Vector4
| Cuat: ,820 ,413 -,365 -,153 | ángu: 099 035 066 111 grados Eje: ,830 ,418- ,369 Ángulo: 198 º
| Matr, valores y ángulos:
Microsoft.Kinect.Matrix4
| ,392 ,789 -,472 ,000 | 067 038 118 090
| ,566 -,612 -,553 ,000 | 056 128 124 090
| -,725 -,050 -,687 ,000 | 136 093 133 090
| ,000 ,000 ,000 1,000 | 090 090 090 000 grados
Compr modulos hori y verti y quat:1,000 1,000 1,000
|Rotaciones Jerárquicas
| Cuat: ,000 ,000 ,859 ,511 | áng: 059 090 090 031 grados Eje: ,000 ,000 1,000 Ángulo: 118 º
| Matr, valores y ángulos:
| -,477 ,879 ,000 ,000 | 118 028 090 090
| -,879 -,477 ,000 ,000 | 152 118 090 090
| ,000 ,000 1,000 ,000 | 090 090 000 090
| ,000 ,000 ,000 1,000 | 090 090 090 000 grados
Compr modulos hori y verti y quat:1,000 1,000 1,000
|
|-------------------------------------------------------------
| Hues: 9. Long (espacial, normal): 020 | 016 cm.
| Arti: de ShoulderRight:8 a ElbowRight:9 | Posi: de 037 -036 263 a 035 -049 248 cm
|Rotaciones Absolutas
Microsoft.Kinect.Vector4
| Cuat: -,645 -,241 ,649 ,324 | ángu: 071 130 104 050 grados Eje:- ,682- ,254 ,686 Ángulo: 142 º
| Matr, valores y ángulos:
Microsoft.Kinect.Matrix4
| ,042 ,731 -,681 ,000 | 088 043 133 090
| -,109 -,675 -,730 ,000 | 096 132 137 090
| -,993 ,105 ,052 ,000 | 173 084 087 090
| ,000 ,000 ,000 1,000 | 090 090 090 000 grados
Compr modulos hori y verti y quat:1,000 1,000 1,000
|Rotaciones Jerárquicas
| Cuat: ,347 -,200 ,050 ,915 | áng: 024 070 102 087 grados Eje: ,860- ,495 ,124 Ángulo: 48 º
| Matr, valores y ángulos:
| ,915 -,047 ,400 ,000 | 024 093 066 090
| -,230 ,754 ,615 ,000 | 103 041 052 090
| -,331 -,655 ,680 ,000 | 109 131 047 090
| ,000 ,000 ,000 1,000 | 090 090 090 000 grados
Compr modulos hori y verti y quat:1,000 1,000 1,000
|
|-------------------------------------------------------------
| Hues: 10. Long (espacial, normal): 020 | 014 cm.
| Arti: de ElbowRight:9 a WristRight:10 | Posi: de 035 -049 248 a 024 -060 235 cm
Rotaciones Absolutas
Microsoft.Kinect.Vector4
 Cuat: -,550 -,080 ,687 ,467 | ángu: 062 123 095 047 grados Eje:- ,622- ,091 ,777 Ángulo: 124 º
| Matr, valores y ángulos:
Microsoft.Kinect.Matrix4
| ,042 ,731 -,681 ,000 | 088 043 133 090
| -,554 -,550 -,625 ,000 | 124 123 129 090
| -,831 ,404 ,382 ,000 | 146 066 068 090
| ,000 ,000 ,000 1,000 | 090 090 090 000 grados
Compr modulos hori y verti y quat:1,000 1,000 1,000
|Rotaciones Jerárquicas
| Cuat: ,237 ,000 ,000 ,972 | áng: 014 076 090 090 grados Eje: 1,000 ,000 ,000 Ángulo: 27 º
| Matr, valores y ángulos:
| 1,000 ,000 ,000 ,000 | 000 090 090 090
| ,000 ,888 ,460 ,000 | 090 027 063 090
| ,000 -,460 ,888 ,000 | 090 117 027 090
| ,000 ,000 ,000 1,000 | 090 090 090 000 grados
Compr modulos hori y verti y quat:1,000 1,000 1,000
 
Rotadores de kesqueleto válidos

Para probar el comportamiento de paámetros de entrada y resultado en ejes y ángulo de estos cuaterniones, introducimos valres equivalentes en la vantana de matrices y cuaterniones y encontramos resultados similares al tomado como ejemplo:

 

Hueso 3

| Cuat: -,087 ,904 -,083 -,410 | ángu: 114 095 025 095 grados Eje:- ,095 ,991- ,091 Ángulo: 228 º
100, 14, 100, 228       y sale    Eje, Ángulo:  -.17,  97  -.17 228 º

 

(absoluto y jeránquico)
 

---

 

Vuelta al Principio    Última actualización: martes, 04 de agosto de 2015    Visitantes: