Esta página está en construcción: perdonen los errores, repeticiones y temas inacabados.

This page is being developed: I am sorry for errors, duplications  and unfinished subjects.

 

 

Proyecto Danzante. Matrices en espacio vectorial 3D (incluido en Danzante)

 

El uso constante de matrices 3D ampliadas en el espacio de esqueletos de la Kinect nos lleva a refrescar estos conceptos. Acudimos primero a nuestros recuerdos, repensando su naturaleza. Refresque si lo desea el concepto de espacio vectorial.

 

Los vectores emergen de representar puntos en un espacio (claro, vectorial) en diferentes sistemas cartesianos de coordenadas, tres ejes mutuamente ortogonales. Y las matrices emergen (entre otras maneras) como forma ordenada (eso es una matriz, una ordenación o disposición de números y algunas operaciones con ellas) cambiar o girar esos vectores o puntos en diferentes sistemas cartesianos de coordenadas.

 

Es decir, si construimos ese sistema cartesiano, y consideramos unos vectores de base unitarios (de tamaño unidad), que llamaremos i,  j,  k , podemos representar un vector  u  también unidad en función de sus proyecciones sobre esos tres vectores de base, como

 

  u  = x .  i + y. j +  z. k  =   cos a . i + cos b . j +  cos g . k 

 

O sea, sus coordenadas en ese sistema son los cosenos de los ángulos que forma el vector con cada uno de esos ejes. Se cumple, evidentemente, por lo tanto:

 

 cos ² a  + cos ² b  +  cos ² g  =  1

 

Si el vector no es unidad y tiene un módulo m, tendremos ahora:

 

 v  =  m. cos a . i + m. cosb . j +  m.cosg . k 

 

Si ahora queremos cambiar de sistema de coordenadas, podemos hacerlo usando las expresiones anteriores: como cada vector de base antiguo tiene una expresión en el sistema nuevo, no tenemos mas que sustituir y encontramos:

 

 v  =  m. cos a . i + m. cosb . j +  m.cosg . k   =

=   m. cos a ( cos a_i' . i ' + cosb_i' . j ' +  cosg_i' . k' )

+  m. cos b . ( cos a_j' . i ' + cosb_j' . j ' +  cosg_j' . k' )

+  m. cos g . ( cos a_k' . i ' + cosb_k' . j ' +  cosg_k' . k' )    =

     m. ( cos a  cos a_i'  + cos b  cos a_j'  + cos g . cos a_k' )   i '  +

+   m. (cos a  cos b_i'   + cos b  cos b_j' . + cos g  cos b_k' ) .  j '   + 

+  m. (cos a  cos g_i'    + cos b .cos g_j' .+  cos g .  cos g_k' .)   k'    =

lo que puede ser puesto en forma de producto de un escalar m por un vector unitario (modulo 1)  1x3 (vector fila), y por una matriz cuadrada 3 x 3:

 

El vector es  

 v   =   [  cos a'   cosb'   cosg'  ]

 siendo sus coordenadas sus cosenos directores en el nuevo sistema; que cumplen igualmente:

 cos ² a'  + cos ² b'  +  cos ² g'  =  1

es decir sus elementos son sus coordenadas originales. Y la matriz es:

[  cos a_i'    cos a_j'  . cos a_k'  ]

[  cos b_i'     cos b_j'    cos b_k'  ]

[  cos g_i'      cos g_j'     cos g_k'   ]

formada por tres vectores columna adosados, cada uno de los cuales  representa las coordenadas de cada vector de base antiguo en el nuevo sistema de coordenadas (ortogonal de vectores unidad  (. i ',   j ',  k ' ) )

 

El resultado es claro, el vector original  v , pero ahora referido al nuevo sistema de coordenadas. 

  v   =   [  cos a    cosb     cosg ]

Pero, podemos adoptar otra interpretación de este proceso: en lugar de pensar en un sólo vector que refereimos sucesivamente a dos sistemas de coordenadas, siendo la matriz citada la que efectúa la conversión, podemos en cambio contemplar lo acaecido como dos vectores en un sólo sistema de coordenadas, siendo ahora la matriz la que nos lleva de uno al otro, la que tyransforma uno en el otro.

 

Por lo tanto, formal y geométricamente, esto también equivale a un giro del vector en el espacio 3D, si pensamos en un único sistema de coordenadas. Ahora los elementos de vectores y matrices

|    v₁   v₂   v₃  |      y

 

|    a₁₁   a₁₂    a₁₃  |

|    a₂₁   a₂₂    a₂₃  |

|    a_{3 1}  a₃₂   a₃₃   |

se refieren a las mismos vectores de base; y las coordenadas ant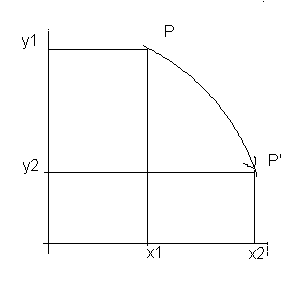iguas y modernas no son mas que las coordenadas de dos vectores diferentes, el original y su girado. Los juegos y operaciones de estos vectores y matrices son los mismos  y únicamente varia nuestra aplicación o interpretación  geométrica e intuitiva.

Veámoslo en dos dimensiones: el punto P está en principio referido a dos ejes perpendiculares, horizontal y vertical, siendo sus coordenadas x1 e y1, respectivamente.

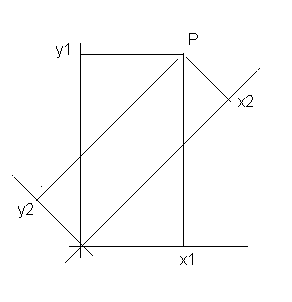
Podemos girar los ejes hacia la izquierda, lo que disminuirá su ordenada, que será ahora y2; y  aumentará su abscisa hasta x2. Pero esa operación es equivalente a girar el mismo ángulo el vector o punto hacia la derecha: las coordenadas se modifica de manera idéntica.

Así que si suprimimos las figuras y la intuición o interpretación geométricas, tenemos un cambio del cual no sabemos en qué consiste. Solo observamos un  cambio en los valores de las coordenadas de un punto o vector. Lo que eso represente en un mundo geométrico le es ajeno a la operación matricial descrita. O, de otra manera, una misma operación matricial admite varias interpretaciones geométricas e intuitivas diferentes. Ello no debe extrañarnos, porque un simple producto puede interpretarse de muchas maneras: cambio de tamaño, escalado, precios de varios productos iguales, cálculo de medias ponderadas...

Continuamos estas reflexiones sobre el relativismo en Sistemas de referencia en el espacio 3D y coordenadas de vectores y, sobre giros y otras operaciones en Movimientos, transformaciones y sus Matrices en espacio vectorial 3D y cuaterniones.

 

---

 

Vuelta al Principio    Última actualización: domingo, 06 de septiembre de 2015    Visitantes: