1. Tres sumandos p, q, r, uno para cada coordenada, que trasladan el punto en cada dimensión, y 2. Un factor de la matriz de giro original, que cambia ese tamaño de las coordenadas por igual. Asív = m . cos a . i + m . cosb . j + m . cosg . k < eq> v = m [ cos a cosb cosg ] quedará ahora trasformado en v ' = h . [ ( m. cos a' + p ) . i + ( m. cos b' + q ) . j + (m . cos g' + r ) . k ) < eq> v' = h . m [ p / m + cosa' q / m + cosb' r / m + cosg' ] ecuación que indica un orden de las operaciones: giro (productos en cada coordenada), desplazamientos (sumandos) y homotecia (factor general para todo. Ese orden de las
 operaciones
ha de quedar definido y fijo en cada caso: no es igual aumentar (por
ejemplo) y luego trasladar, que lo contrario: los valores de los
parámetros son diferentes, lo que se refleja en las ecuaciones
anteriores en la situación de los factores m (modulo), h (razón de
homotecia) y sumandos p, q, r desplazamientos en cada coordenada).
Si aumento primero, los desplazamientos
han de ser mayores (multiplicados por el factor h) que al revés. En
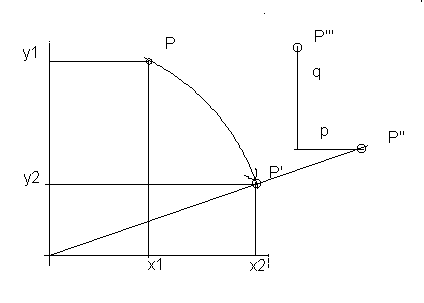
la figura se muestran, en el plano (espacio 2D) las tres
operaciones, en el orden Giro-Homotecia-Traslación, con valores
respectivos del ángulo de giro negativo, factor de homotecia mayor
que 1, y desplazamientos de abscisa negativo y ordenada positiva.
Con parámetros adecuados eliminamos
cada uno de los movimientos descritos: h =1 suprime la homotecia,
ángulo de giro nulo suprime el giro, desplazamientos nulos suprimen
la traslación. Y anulando dos de las tres operaciones encontramos
separadas cada una de ellas.
Si ahora queremos cambiar de
sistema de coordenadas, podemos hacerlo usando las expresiones
en anteriores vistas en
Matrices en espacio vectorial 3D (vector antiguo en función de
los nuevos). Pero ampliándolas ahora con el sumando
de traslación. No tratamos por ahora la homotecia ( h = 1), y
consideramos vectores unitarios (módulo 1, coordenadas iguales a
cosenos ( entre 0 y 1).
operaciones
ha de quedar definido y fijo en cada caso: no es igual aumentar (por
ejemplo) y luego trasladar, que lo contrario: los valores de los
parámetros son diferentes, lo que se refleja en las ecuaciones
anteriores en la situación de los factores m (modulo), h (razón de
homotecia) y sumandos p, q, r desplazamientos en cada coordenada).
Si aumento primero, los desplazamientos
han de ser mayores (multiplicados por el factor h) que al revés. En
la figura se muestran, en el plano (espacio 2D) las tres
operaciones, en el orden Giro-Homotecia-Traslación, con valores
respectivos del ángulo de giro negativo, factor de homotecia mayor
que 1, y desplazamientos de abscisa negativo y ordenada positiva.
Con parámetros adecuados eliminamos
cada uno de los movimientos descritos: h =1 suprime la homotecia,
ángulo de giro nulo suprime el giro, desplazamientos nulos suprimen
la traslación. Y anulando dos de las tres operaciones encontramos
separadas cada una de ellas.
Si ahora queremos cambiar de
sistema de coordenadas, podemos hacerlo usando las expresiones
en anteriores vistas en
Matrices en espacio vectorial 3D (vector antiguo en función de
los nuevos). Pero ampliándolas ahora con el sumando
de traslación. No tratamos por ahora la homotecia ( h = 1), y
consideramos vectores unitarios (módulo 1, coordenadas iguales a
cosenos ( entre 0 y 1).
v = cos a . i + cosb . j + cosg . k =cos a ( cos ai' . i ' + cos bi' . j ' + cos gi' . k' ) + cos b . ( cos aj' . i ' + cos bj' . j ' + cos gj' . k' ) + cos g . ( cos ak' . i ' + cos bk' . j ' + cos gk' . k' ) + p . i ' + q . j ' + r . k'
=
lo que puede ser puesto en forma de producto de un vector 1x4 (vector fila) unitario (modulo 1), por una matriz cuadrada 4 x 3: Los vectores inicial y final son los ya conocidos (h=1, m=1), ampliados con una nueva coordenada o componente, por ahora = 1( cos a .cos ai' + cos b cos aj' + cos g .cos ak' + p ) . i ' + + ( cos a cos bi' + cos b cos bj' + cos g cos bk' + q ) . j ' + (5) + ( cos a cos gi' + cos b .cos gj' + cos g cos gk' + r ) . k'
siendo sus coordenadas sus cosenos directores respectivamente en el antiguo y el nuevo sistema. Llamamos v y v ' a ambos entes, diferentes en tanto tales. El que representen el mismo en nuestra intuición geométrica no cambia ese hecho formal. Son diferentes porque lo son sus coordenadas. Y la matriz es:v = [ cos a cosb cosg 1 ] v ' = [ cos a' cosb' cosg' 1 ]
formada por tres vectores columna de 4x1 adosados, cada uno de los cuales representa las coordenadas de cada vector de base antiguo en el nuevo sistema de coordenadas (ortogonal de vectores unidad, i ', j ', k ' ) en las tres primeros elementos, y en el cuarto una constante que representa el desplazamiento o traslación en cada una de las tres coordenadas; de tal manera que el producto del vector fila por la matriz (en ese orden) nos reconstruye la ecuación (5). Así, tenemos v = M × v ', representando aquí × el producto matricial usual de filas por columnas: f i × c j = a ij. Alternativamente podemos usar vectores columna 1x4, transpuestos pues de los anteriores fila, y transponer asimismo la matriz para que se nos reconstruya, ahora también, la ecuación 5.[ cos ai' cos aj' . cos ak' 0 ] [ cos bi' cos bj' cos bk' 0 ] [ cos gi' cos gj' cos gk' 0 ] [ p q r 1 ]
En los parámetros que envía la cámara Kinect, encontramos (Ángulos de los huesos V) matrices comov T = MT × v 'T
[ cos a ] [ cos b ] [ cos g ] [ 1 ] = [ cos ai' cos bi' cos gi' p ] [ cos aj' cos bj' cos gj' q ] [ cos ak' cos bk' cos gk' r ] [ 0 0 0 1 ] × [ cos a ' ] [ cos b ' ] [ cos g ' ] [ 1 ]
lo que quiere decir que el desplazamiento es nulo (fila inferior nula para tres vectores columna de las tres coordenadas). El 4º vale 1, quizá para permitir operaciones de manera cómoda. Por cierto, se cumple que la suma de cuadrados de los cosenos en los vectores columna y en los vectores fila de la matriz 3x3 superior, es en efecto 1. Cuat es el cuaternión correspondiente a la matriz. Así que la ampliación a 4 del orden 3 de vectores y matrices en el espacio 3D no tiene más función que ampliar las ecuaciones de giro para incluir también una (posible) traslación, y todo ello, usando las operaciones tradicionales de cálculo matricial. pero, naturalmente, seguimos en un espacio 3D, no 4D. En realidad, las matrices son de orden 4x3 o 3x4, mientras que los vectores o puntos tienen tres coordenadas efectivas y una ficticia, solo útil para cumplir con las reglas de producto matricial. Si renunciamos a la traslación (que puede realizarse, antes o después, en operación independiente, volvemos al orden 3 con idénticas propiedades de giro: la última ecuación matricial puede escribirse:| Rotaciones Absolutas
| Cuat: -0,179 0,504 0,614 0,580 | ángu: 100 060 052 055 grados
| Matr, valores (cosenos) y ángulos:
|-0,428 0,412 0,804 0,000 | 115 066 036 090
| 0,826 -0,182 0,533 0,000 | 034 100 058 090
| 0,366 0,893 -0,263 0,000 | 069 027 105 090
| 0,000 0,000 0,000 1,000 | 090 090 090 000 grados
[ cos a ] [ cos b ] [ cos g ] = [ cos ai' cos bi' cos gi' p ] [ cos aj' cos bj' cos gj' q ] [ cos ak' cos bk' cos gk' r ] × [ cos a ' ] [ cos b ' ] [ cos g ' ]