Continuando lo
comentado en
Dos cámaras Kinect simultaneas I, y
II,
III y
IV. vamos a comprender y realizar parcialmente lo descrito en la
última de esas páginas.
Para ello,
emplearemos una sóla c´mara y dos imágenes de un esqueleto , la
primiva ofrecida por la cámara Kinect y esa misma trnsformada
mediante una matriz cualquiera de giro. Haast ahora las obtenemos de
las rotaciones absolutas de huesos, como hemos visto enProyecto
Danzante. Matrices en espacio vectorial 3D.htm
Se trata de
hacer corresponder las imágenes del mismo danzante procedentes de en
cada cámara, en una solo imagen que recoja las posiciones de las
articulaciones en cada una, pero de manera inteligente, bien
eligiendo la mejor, bien combinando de alguna manera la doble
información.
Hay dos
tareas principales que suponen dos suposiciones contrarias:
1. Calibrar
las cámaras. Consiste en llevar ambas imágenes a una, es decir,
superponerlas. Ello requiere en esencia tres operaciones:
1. La primera es trasladar una de ellas a un punto homólogo. Puede ser el centro del esqueleto, la articualcion 0, sie se trata de esqueleto completo (la 2 si es el 'esqueleto sentado', incompleto con articulaciones hasta la 11. 2. La segunda es girar ese esos esqueletos en el espacio. Son tres dimensiones, pero como están ligadas, con Dos Giros es suficiente. Podemos elegir las coordenadas geográficas, azimut y Altura.. En la nomenclatura Kinect, ello supone girar primero en el plano XZ, plano horizontal, sin ángulo AZI. Y, eje vertical, y después en el plano creado por el primer giro y el eje y, eje perpendicular al plano que forma con el vertical de referencia el ángulo AZI anterior, girar otro ángulo ALTU, 3. La tercera es aplicar una semejanza u homotecia a los esqueletos, o sea aumentar o disminuir sus tamaños hasta que coincidan. Hay que recordar que Kinect mide las coordenadas de cada punto como lo hace el ojo en cuanto a tamaño, objetos lejanos se ven pequeños: cuanto mayor es Z, menores son las X e Y aparentes.Es lógico, para ahorrar operaciones, no llevar a ambos esuqñetos al mismo punto sino al origen de uno de ellos, con lo que simplificamos el trabajo total. Las operaciones anteriores suponen dos esqueletos correctos, es decir rigurosamente semejantes. Si ello es así se puede con tiauñ seguridad jjevar a cano las operaciones anteriores mediante una comparación continua de las distancias entre ambios esqueltos: la suma de distancias absolutas entyre sus articulaciones homólogas. Ello sería la p-nom e a1 pero podemos usar otras valores p, como 2, la distancia geométrica en el espacio. Si lo esqueletos no son perfectos el proceso anterior debe realizarse estadísticamente, es decir, para evaluar los acercaminetos entre eloos 8p´distancia) debemos tomar la media de esas distancias pareticulares entre articulaciones homólogas y ello, en sucesivas parejas de esqueletos, hasta que la ley de los grandes números nos lleve a un compromiso. este compromiso seráelmímo alcanzable, una bola de tamaño irreductible. El error sistemático ligado a la imprecisión de los esqueltos. A este respecto debemos recordar que los errores en cada coordenada se ordenan de amyor a menos en Y, X, Z, según se comprobó con la captación de maniquies (ver) . Lo esqueltops no son perfecto sporque La capracion de coordenadas no es exacta de dios maneras aparentemente:: Hay eerrores de captacion debidas a una erronea estimacion de laa situacion de las articlaciones. Kinect no ¡ve' las articuilacioners, las deduce de la figura de profundifasd, a parftir de una (gran?) base de datos de imágnes de personas en diferentes posturas) la cámara entonces ha adistrado su ojo para detyectar articulaciones, cono el ojo de un ahumano detecta la belleza de una mujer aunque esté vestida con miriñaques y capas. Eval´çua y mide a aprtir de pistas, pistas que le prtoporciona un alarha experiencia en mirar con interés.: su base de datos de nellezar y feezas.
1. .Se capta una posición correcta con errores. 2. Se capta un posición incorrecta por estimación errónea.Aunquye quiza ambos errores sean el m ismo, a efectos prácticos debemos dividir en esas categorías y tratarlos diferentemente. La bola es debida a que no podemos acercarnos indefinidamente al cero en la diferencia de valortes. En el método de obtencios de una raiz de Newton Cramner, vamos obteniendo el valor de la variable al acercarnos al cero. Suponiendo una funcion monótona y continuia. Pero el error sistematico en esa funcion la conv ierte en un alínra gorda, o mejor en una zona imprecisa de anxchura constante q cuyos limtes son paraleos a la linea ezactqa sin grosar- El radio de eta bola de error, no obstante será pequeño (¿ quizá cercano al milímetro?) porque La calibracion obtiene una matriz de trasgormacion de coordenadas que ellebva una de la simagenes sobre la otra. esa matriz lleva un factor, el módiulo m que multiplica a una matriz unitaris (vectores de base unidad) En el futura, esa matriz unirá las parjes homógas en el tiempo y decidira qué combinacion de ambas es la probablemente corresta. Pero, a efectso de dibujo o representacion únicamnte, el uso de coordenadas relativas al centro ya nos superpone ambos centros, ya que ambos se colocan en el centro de la pantalla previamente elegido. Esto se verá en DcKS V.Fundir sus imagenes las operaciones anteriores se realizan informáticamente mediante las librerías de funciones y objetos que NET de Microsoft ofrece para ello Kinect, por supuesto, y Media3D. Se tratan en varias páginas, como Cuaterniones, Matrices como operadores o como entes, Movimientos y transformaciones en plano y espacio. Descripción geométrica. Veamos el proceso, ahora (enero 2016) muy muy mejotado
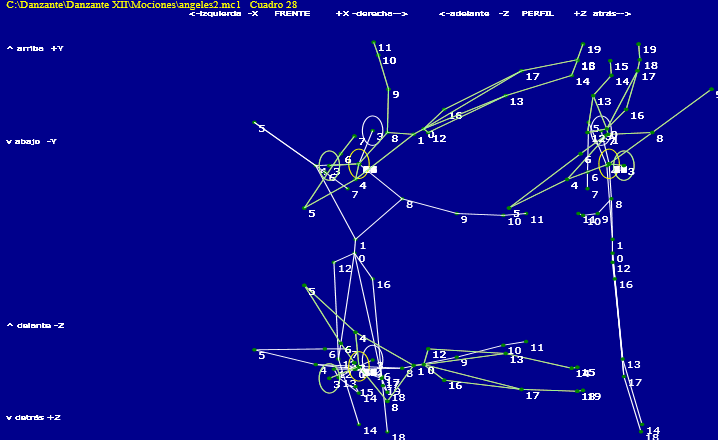 |
Posicion incial de esqueleto original, en blanco y rotado con matriz desconocida (genetada aleatoriamente con escalado y giro sucesivos, es ese orden | |
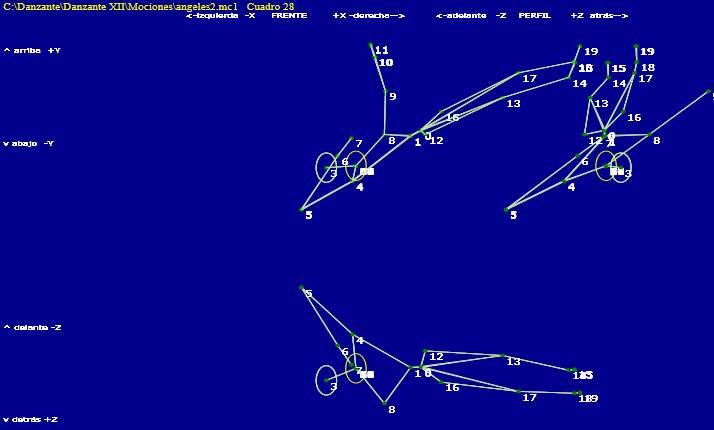
| Posicion final de la reunion | Informaciones de los últimos giro y escalado | |
 |
|
|
|
Moción:
C:\Danzante\DanzanteXII\Mociones\angeles2.mc1
Cuadro: 28 Momentos 0, 1: 1 1 Aproximación doble nº: 1 Aproximación doble nº: 2 Aproximación doble nº: 3 Aproximación doble nº: 4 Aproximación doble nº: 5 giros Dist: Ini= 1251 111,0º | 130,0º Busca=01 mm| 00,0º | 00,0º Resultados Giro: Cota_distan: 1 ángulo salto: 0.25 salto increm: 0.1 Dt_mm ruido: 0 Pasos: 3 Arti usadas: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 Arti no usadas: Incog eje:0;1;0 Estim eje:-0,106604429569519;-0,378039551831008;-0,91963122655093 Incog angle:0 Estim angle:38,6486229921007 Incog :Identity | Cuat: ,000 ,000 ,000 1,000 | áng: 000 090 090 090 grados Eje: 090 000 090 Ángulo: 0 º Estim : | Cuat: -,035 -,125 -,304 ,944 | áng: 019 092 097 108 grados Eje: 096 112 157 Ángulo: 39 º Incog mat: | 1,000 ,000 ,000 ,000 | 000 090 090 090 | ,000 1,000 ,000 ,000 | 090 000 090 090 | ,000 ,000 1,000 ,000 | 090 090 000 090 | 1,000 | 000 grados Estim mat: | ,783 ,583 -,215 ,000 | 038 054 102 090 | -,566 ,812 ,143 ,000 | 124 036 082 090 | ,258 ,010 ,966 ,000 | 075 089 015 090 | 1,000 | 000 grados Coci1 : | 1,000 ,000 ,000 ,000 | 000 090 090 090 | ,000 1,000 ,000 ,000 | 090 000 090 090 | ,000 ,000 1,000 ,000 | 090 090 000 090 | 1,000 | 000 grados Coci2 : | 1,000 ,000 ,000 ,000 | 000 090 090 090 | ,000 1,000 ,000 ,000 | 090 000 090 090 | ,000 ,000 1,000 ,000 | 090 090 000 090 | 1,000 | 000 grados |
Moción: C:\Danzante\Danzante XII\Mociones\angeles2.mc1 Cuadro: 28 Momentos 0, 1: 1 1 Aproximación doble nº: 1 Aproximación doble nº: 2 Aproximación doble nº: 3 Aproximación doble nº: 4 Aproximación doble nº: 5 escala Dist: Ini= 1251 111,0º | 130,0º Busca=01 mm| 00,0º | 00,0º Resultados Escalado: Cota_distan: 1 porcentaje_salto: 0.0833333333333333 salto increm: 1 Dt_mm ruido: 0 Pasos: 2 Arti usadas: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 Arti no usadas: Incog eje:0;1;0 Estim eje:-0,106604429569519;-0,378039551831008;-0,91963122655093 Incog angle:0 Estim angle:38,6486229921007 Incog :Identity | Cuat: ,000 ,000 ,000 1,000 | áng: 000 090 090 090 grados Eje: 090 000 090 Ángulo: 0 º Estim : | Cuat: -,035 -,125 -,304 ,944 | áng: 019 092 097 108 grados Eje: 096 112 157 Ángulo: 39 º Incog mat: | 1,000 ,000 ,000 ,000 | 000 090 090 090 | ,000 1,000 ,000 ,000 | 090 000 090 090 | ,000 ,000 1,000 ,000 | 090 090 000 090 | 1,000 | 000 grados Estim mat: | ,783 ,583 -,215 ,000 | 038 054 102 090 | -,566 ,812 ,143 ,000 | 124 036 082 090 | ,258 ,010 ,966 ,000 | 075 089 015 090 | 1,000 | 000 grados Coci1 : | 1,000 ,000 ,000 ,000 | 000 090 090 090 | ,000 1,000 ,000 ,000 | 090 000 090 090 | ,000 ,000 1,000 ,000 | 090 090 000 090 | 1,000 | 000 grados Coci2 : | 1,000 ,000 ,000 ,000 | 000 090 090 090 | ,000 1,000 ,000 ,000 | 090 000 090 090 | ,000 ,000 1,000 ,000 | 090 090 000 090 | 1,000 | 000 grados |
Nótese la aproximacion muy grande, en negrita: 1 mm de media |
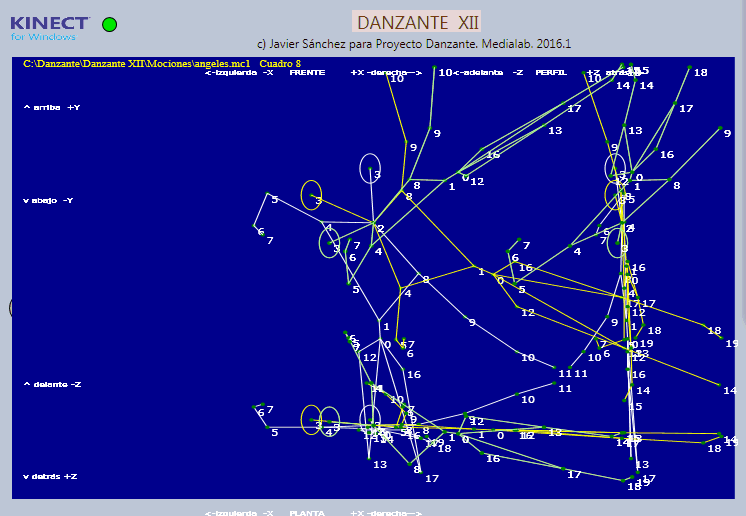 |
Otro caso: etapa intermedia
distancia media era 55 mm. en este estadio verde. incognita
amarillo, buscando
blaco, inicial, origen |
|