Estudios sobre Riges: Mosaico 1 (perteneciente a Decoración Geométrica Islámica)

Incluido en estudios sobre Riges

La estudiamos porque usa distancias de tamaño variado, es decir, no solo las típica a y c y sus mitades, sino además las diferencias a-c y c-a/2.

Encontramos entre nuestros papeles una fotocopia de la figura adjunta. Sabiendo que hay 8 direcciones de los bordes de las mosaicos, es decir, es una red8, asignamos las distancias según aparece en la figura, la serie horizontal y la oblicua, según se define en Disegno de redes de 8. Con esas semisecuencias dibujamos la red, que codificamos asçi:

Red 8. H [//çacácáç: 7] X [//çacácácaç: 9]. sX[ 3a+ 4c ] sH[ 2a+ 3c ]. Dispos: dx=1. dy=1. dz=0.

Añadimos otras distancia dividiendo el primer a, en ambos:

Red 8. H [//çáácácáç: 8] X [//çáácácácaç: 10]. sX[ 3a+ 4c ] sH[ 2a+ 3c ] Ss oblicua no es capicúa.. Dispos: dx=1. dy=1. dz=0.

Pero no es sufuciente, porque los pequeños picos de los azafates harpados y otras figuras nuevas en el repertorio habitual de las Riges no son cubiertos por la red. DE modo que dividimos en ambas sss la interdistancia a en la suma de á y â, que en nuestro código valen c.-a/2 y a/2, en valores aproximados de .3 y .7. Los harpados aparecen ya bie, según demuestra la figura dos, en la que coloreamos a mano las figuritas difíciles.

No es perfecto porque no se cumplen todavía las condiciones de red periódica, pero nos sirve para reflejar la figura. La codificación es la siguiente, con los comentarios críticos que nuestro programa añade a nuestro diseño (al proponer la red, el programa analiza si se cumplen las leyes de red periódica de 8, en Redes periodicas de 8):

Red 8. H [//çáácáàááç: 9] X [//çáácáàáácaç: 11]. sX[ 4.5a+ 2.5c ] sH[ 3.5a+ 1.5c ] Num. de 'a' en oblicuo ha de ser igual a Num. de 'c' en recto Num. de 'c' en oblicuo ha de ser doble que Num. de 'a' en recto Ss oblicua no es capicúa.. Dispos: dx=1. dy=1. dz=0.

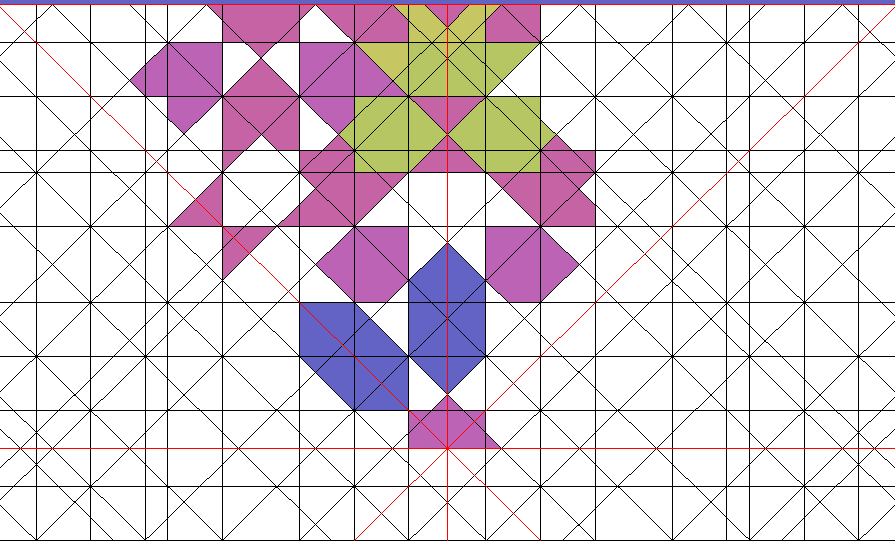Fig.2 Red 8. H [//çáácáàááç: 9] X [//çáácáàáácaç: 11]. sX[ 4.5a+ 2.5c ] sH[ 3.5a+ 1.5c ]

Caso resuelto en cuanto a la red. No programamos por el momento la Rige con cintas o con meros bordes.