Esta página está en construcción: perdonen los errores, repeticiones y temas inacabados.

This page is being developed: I am sorry for errors, duplications  and unfinished subjects.

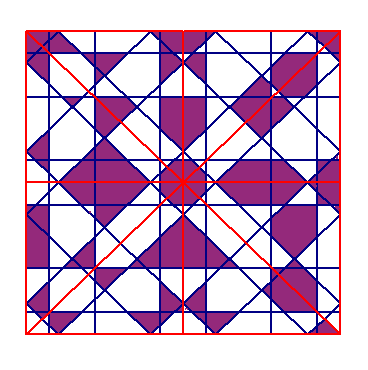
Polígonos simétricos en red N  (perteneciente a Decoración Geométrica Islámica)

En el estudio de las Riges (redes islámicas geométrica entrelazada) se observa la preferencia de los diseñadores por figuras o losas simétricas, es decir, que admiten al menos un eje de simetría. Naturalmente el eje de simetría, si es único, debe pasar necesariamente en los polígonos de un número impar de lados por el único ángulo desigual, que no tiene pareja. En los pares en cambio puede pasar por vértices o por centros de lados (en este caso por lados perpendiculares al eje. Y por supuesto puede haber hasta 2 N ejes, en los regulares. En la figura adjunta marcamos algunos de los posibles polígonos simétricos generados en una red de N=8, comprobándose la aparición de formas regulares o no regulares, con forma que recuerda objetos o animales, o formas nuevas, pero todas al menos con un eje de simetría, aunque algunas, los polígonos regulares convexos o estrellados admiten hasta 16, el doble de N.  La mayoría son compactas es decir con pocos salientes. Encontramos pues triángulos, cuadrados, rectángulos, estrellas junto a puntas de flecha, de lanza, diábolos y varias más, aunque no se han marcado todas. Pero encontramos interesante encontrarlas, todas esas figuras simétricas, convexas (en general, pero necesariamente) y conexas (sin cruces de lados) posibles en la red N.

Comparamos con el número de regulares. Las posibilidades aumentan con N, pero no regularmente. Por ejemplo, calculando todos los polígonos convexos (ángulos interiores menores que dos rectos (180º), y limitando el número de lados al doble del orden de la red (o limitándolo a polígonos de 12 lados), encontramos (mediante Metabolé, Poligonos simetrico, PU21 ) la tabla siguiente.  Pero hay que tener en cuenta que sólo contamos combinaciones de ángulos y no su orden en el perímetro, lo cual ofrece más figuras simétricas permutando las parejas de ángulos iguales (simétricos). Pensemos en figuras más panzudas o más esbeltas). En principio tomamos lados iguales mientras sea posible, porque suele haber uno o dos mayores que el resto para evitar cruces en el perímetro, lo que da lugar a polígonos de interior no conexo, o sea, polígonos múltiples, varios unidos por sus vértices. Vea la tabla y el gráfico adjuntos : ( Cambiar etiquetas mal)

tipo   \    N	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26
regulares	3 ?	1	1	2	1	2	2	2	1	4	1	2	3	3	1	4
simétricos convexos todos
simétricos convexos p<17	1	1	2	4	3	8	5	14	7	22	10	35	14	49	18	73	23	98	30	137	37	178	43	238
simétricos convexos p<2N	1	1	2	4	4	8	6	14	9	22	13	37	19	54	25	82	34	114	45	164	58	220	74	304
simétricos todos	1	2	7	33	20	100	46	349	91	723	164

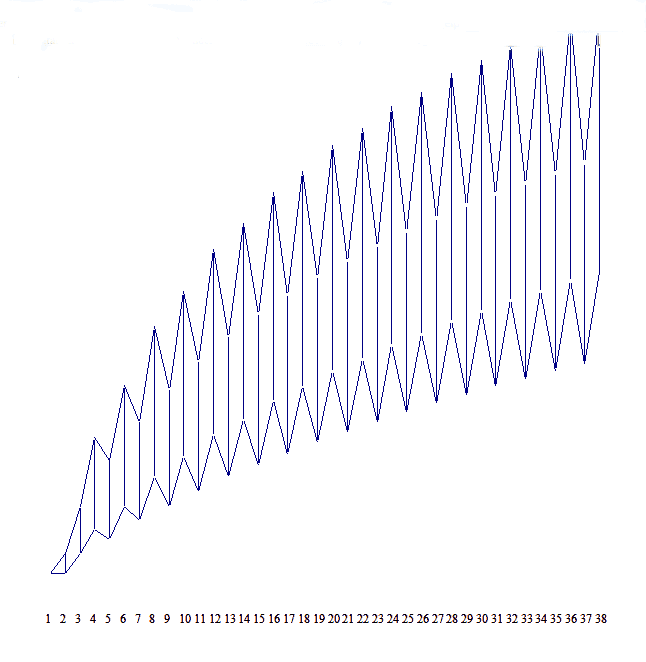
El logaritmo del  número de simétricos en función de N dibuja una curva muy regular, dentada con las crestas en los pares y valles los impares. La envolvente es decrecientemente creciente, como una piedra lanzada arriba y adelante:

	Simétricos convexos N 3 Total sime= 1 N 4 Total sime= 1 N 5 Total sime= 2 N 6 Total sime= 4 N 7 Total sime= 3 N 8 Total sime= 7 N 9 Total sime= 5 N 10 Total sime= 14 N 11 Total sime= 7 N 12 Total sime= 22 N 13 Total sime= 10 N 14 Total sime= 35 N 15 Total sime= 14 N 16 Total sime= 49 N 17 Total sime= 18 N 18 Total sime= 73 N 19 Total sime= 23 N 20 Total sime= 98 N 21 Total sime= 30	N 22 Total sime= 137 N 23 Total sime= 37 N 24 Total sime= 178 N 25 Total sime= 46 N 26 Total sime= 238 N 27 Total sime= 56 N 28 Total sime= 301 N 29 Total sime= 68 N 30 Total sime= 391 N 31 Total sime= 81 N 32 Total sime= 483 N 33 Total sime= 97 N 34 Total sime= 611 N 35 Total sime= 114 N 36 Total sime= 743 N 37 Total sime= 134 N 38 Total sime= 920 N 39 Total sime= 156 N 40 Total sime= 1101	Todos simétricos N 3 Total sime= 1 N 4 Total sime= 2 N 5 Total sime= 7 N 6 Total sime= 33 N 7 Total sime= 20 N 8 Total sime= 100 N 9 Total sime= 4 N 10 Total sime=349 N 11 Total sime= 9 N 12 Total sime= 723 N 13 Total sime= 164 N 14 Total sime= 1726 N 15 Total sime= 275 N 16 Total sime= 2959 N 17 Total sime= 433 N 18 Total sime= 5759 N 19 Total sime= 653 N 20 Total sime= 8846	N 21 Total sime= 948 N 22 Total sime= 15185 N 23 Total sime= 1333 N 24 Total sime= 21700 N 25 Total sime= 1826 N 26 Total sime= 34173 N 27 Total sime= 2445 N 28 Total sime= 46386 N 29 Total sime= 3209 N 30 Total sime= 68653 N 31 Total sime= 4141 N 32 Total sime= 89672 N 33 Total sime= 5263 N 34 Total sime= 126586 N 35 Total sime= 6599 N 36 Total sime= 160488 N 37 Total sime= 8175 N 38 Total sime= 218322 N 39 Total sime= 10019 N 40 Total sime= 270272
Número de polígonos de 12 o menos lados en red N. Curva de arriba, todos los simétricos, abajo sólo convexos. Ambas curvas representan el logaritmo del número de polígonos (valores exactos a la derecha). Sólo se cuenta un polígono por cada combinación de ángulos (no de cuentan las permutaciones como diferentes).:	Simétricos convexos		Todos los simétricos (con un eje de simetría al menos)

 

En realidad para obtener todos hay que encontrar el mayor número de lados que puede encontrarse en una red N. Y este número es igual que el de regulares: N para pares y 2N para impar, como muestra la segunda casilla de la tabla siguiente. Esto puede comprenderse observando cuanto se cierra un polígono al recorrer sus ángulos es decir, cuanto giran sus lados hacia adentro al recorrerlos. El mínimo corresponde a un ángulo interior máximo, es este no puede llegar al llano, luego vale el entero inferior a N/2.

Además ese número de alcanza sólo con un regular porque cualquier otro va a emplear algún ángulo menor que ese máximo y entonces se cierra mas lo que le hace 'perder lados.

N 3 Total sime= 2 mayor: 6 N 4 Total sime= 1 mayor: 4 N 5 Total sime= 4 mayor: 10 N 6 Total sime= 3 mayor: 6 N 7 Total sime= 8 mayor: 14 N 8 Total sime= 5 mayor: 8 N 9 Total sime= 13 mayor: 18 N 10 Total sime= 9 mayor: 10 N 11 Total sime= 20 mayor: 22 N 12 Total sime= 13 mayor: 12 N 13 Total sime= 30 mayor: 26 N 14 Total sime= 20 mayor: 14 N 15  Total sime= 44 mayor: 30 N 16 Total sime= 27 mayor: 16 N 17 Total sime= 61 mayor: 34	N 3 [ 3 6| 1 1 1 1 1 1]  mayor: 6 N 4 [ 4 4| 1 1 1 1]  mayor: 4 N 5 [ 5 10| 2 2 2 2 2 2 2 2 2 2]  mayor: 10 N 6 [ 6 6| 2 2 2 2 2 2]  mayor: 6 N 7 [ 7 14| 3 3 3 3 3 3 3 3 3 3 3 3 3 3]  mayor: 14 N 8[ 8 8| 3 3 3 3 3 3 3 3] mayor: 8
	Máximos son regulares

Esa regularidad sugiere una ley, una función de N, analítica, es decir, expresable mediante funciones del análisis matemático: las cuatro reglas, raíces y exponenciales, logaritmos, funciones trigonométricas, y otras más extrañas aún. Pero en principio podemos suponer relaciones sencillas, sugeridas por la geometría.

En efecto, a partir de un polígono simétrico, siempre podemos encontrar otro de orden N+2 cortando simplemente dos esquinas con las dos nuevas direcciones, lo que añade un número de polígonos nuevos igual al que ya había, es decir, nos encontramos con el doble. (aunque una rápida inspección de los números en la tabla indica que el crecimiento es menor que ese doble; si fuera igual la  gráfica correspondiente -la inferior- sería una recta -son logaritmo). Esa construcción permite hallar rápidamente todos lo polígonos deseados, lo cual es útil porque los tiempos de cálculo, sólo comprobar que la suma de ángulos interiores vale 2(p-2) rectos y poco más, crece geométricamente con p. Para p=16 el tiempo ya es mayor que la hora en un computador portátil rápido de 2010.

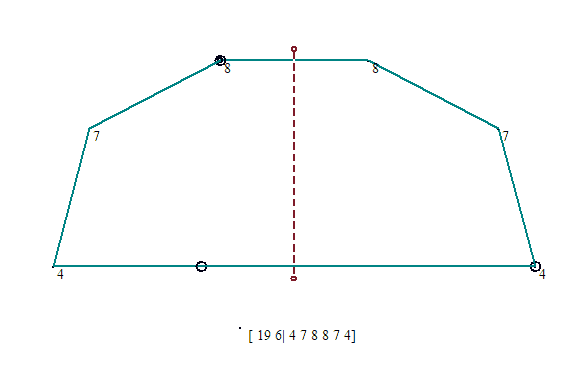
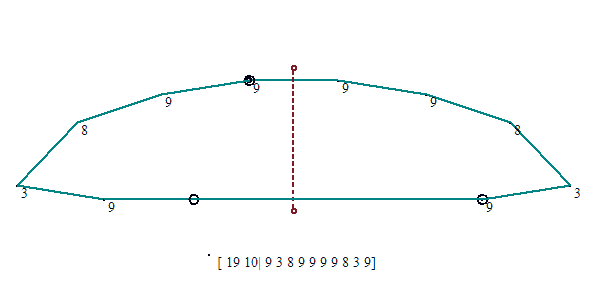
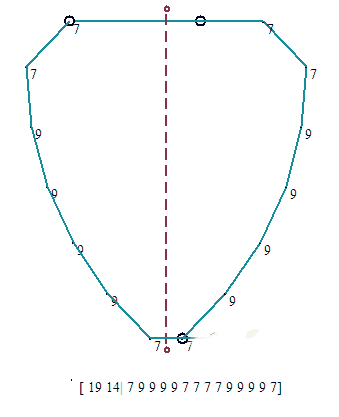
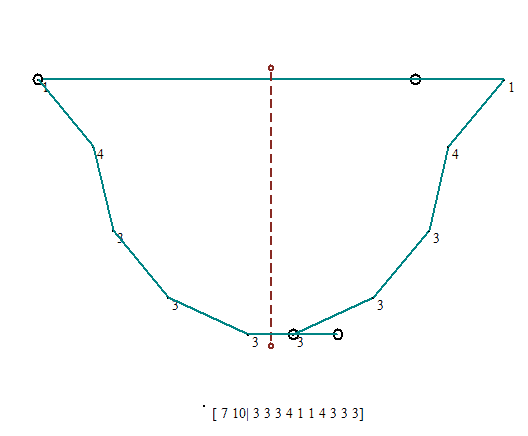
Veamos algunas figuras simétricas y sus códigos. Se escribe el orden N de la red, el número de ángulos del polígono (igual que el de lados), y los índices de los ángulos, es decir, el  número de subdivisiones de la circunferencia en N partes. El primero, de orden 3, usa sólo múltiplos de 360/3, es decir, 120º, que corresponde al índice 1. El índice n/2 no aparece ya en los polígonos convexos, pero puede aparecer en los que no lo son. Sólo son posible pues los índices 1 y 2 en la red N 3.

Nótese que los lados son hasta cierto punto arbitrarios, siempre que se conserve la simetría axial (de eje vertical en este caso). En estos casos intentamos lados desiguales (conservando la simetría).

 

Los datos, son:

regulares	N [p1 k1 i1 q1 si1][p2 k2 i2 q2 s12] ... 3 [ 6 .5 1 3 0] 1 poli 4 [ 4 1 1 4 0] 1 poli 5 [ 10 .5 2 2.5 0] 1 poli 6 [ 3 2 1 6 0] [ 6 1 2 3 0] 2 poli 7 [ 14 .5 3 2.33 0] 1 poli 8 [ 4 2 2 4 0] [ 8 1 3 2.67 0] 2 poli 9 [ 6 1.5 3 3 0] [ 18 .5 4 2.25 0] 2 poli 10 [ 5 2 3 3.33 0] [ 10 1 4 2.5 0] 2 poli 11 [ 22 .5 5 2.2 0] 1 poli 12 [ 3 4 2 6 0] [ 4 3 3 4 0] [ 6 2 4 3 0] [ 12 1 5 2.4 0] 4 poli 13 [ 26 .5 6 2.17 0] 1 poli 14 [ 7 2 5 2.8 0] [ 14 1 6 2.33 0] 2 poli 15 [ 6 2.5 5 3 0] [ 10 1.5 6 2.5 0] [ 30 .5 7 2.14 0] 3 poli 16 [ 4 4 4 4 0] [ 8 2 6 2.67 0] [ 16 1 7 2.29 0] 3 poli 17 [ 34 .5 8 2.13 0] 1 poli 18 [ 3 6 3 6 0] [ 6 3 6 3 0] [ 9 2 7 2.57 0] [ 18 1 8 2.25 0] 4 poli 19 [ 38 .5 9 2.11 0] 1 poli 20 [ 4 5 5 4 0] [ 5 4 6 3.33 0] [ 10 2 8 2.5 0] [ 20 1 9 2.22 0] 4 poli 21 [ 6 3.5 7 3 0] [ 14 1.5 9 2.33 0] [ 42 .5 10 2.1 0] 3 poli 22 [ 11 2 9 2.44 0] [ 22 1 10 2.2 0] 2 poli 23 [ 46 .5 11 2.09 0] 1 poli 24 [ 3 8 4 6 0] [ 4 6 6 4 0] [ 6 4 8 3 0] [ 8 3 9 2.67 0] [ 12 2 10 2.4 0] [ 24 1 11 2.18 0] 6 poli 25 [ 10 2.5 10 2.5 0] [ 50 .5 12 2.08 0] 2 poli 26 [ 13 2 11 2.36 0] [ 26 1 12 2.17 0] 2 poli
simétricos	N [p1 k1 lado11 112...][p2 k2 lado21 lado22... ] ... N 3 |p 3 || |p 4 || |p 5 || |p 6 || [ 3 6| 1 1 1 1 1 1] Total sime= 1 N 4 |p 3 || |p 4 || [ 4 4| 1 1 1 1] |p 5 || |p 6 || |p 7 || |p 8 || Total sime= 1 N 5 |p 3 || |p 4 || |p 5 || |p 6 || [ 5 6| 1 1 2 2 2 2] |p 7 || |p 8 || |p 9 || |p 10 || [ 5 10| 2 2 2 2 2 2 2 2 2 2] Total sime= 2 N 6 |p 3 || [ 6 3|U 1 1 1] |p 4 || [ 6 4| 1 1 2 2] |p 5 || [ 6 5|U 1 2 2 2 2] |p 6 || [ 6 6| 2 2 2 2 2 2] |p 7 || |p 8 || |p 9 || |p 10 || |p 11 || |p 12 || Total sime= 4 N 7 |p 3 || |p 4 || |p 5 || |p 6 || [ 7 6| 1 1 3 3 3 3] [ 7 6| 2 2 2 2 3 3] |p 7 || |p 8 || |p 9 || |p 10 || [ 7 10| 2 2 3 3 3 3 3 3 3 3] |p 11 || |p 12 || |p 13 || |p 14 || Total sime= 3 N 8 |p 3 || [ 8 3| 1 1U 2] |p 4 || [ 8 4| 1 1 3 3] [ 8 4| 2 2 2 2] |p 5 || [ 8 5|U 2 2 2 3 3] |p 6 || [ 8 6| 2 2 3 3 3 3] |p 7 || [ 8 7|U 2 3 3 3 3 3 3] |p 8 || [ 8 8| 3 3 3 3 3 3 3 3] |p 9 || |p 10 || |p 11 || |p 12 || |p 13 || |p 14 || |p 15 || |p 16 || Total sime= 7 N 9 |p 3 || |p 4 || |p 5 || |p 6 || [ 9 6| 1 1 4 4 4 4] [ 9 6| 2 2 3 3 4 4] [ 9 6| 3 3 3 3 3 3] |p 7 || |p 8 || |p 9 || |p 10 || [ 9 10| 2 2 4 4 4 4 4 4 4 4] [ 9 10| 3 3 3 3 4 4 4 4 4 4] |p 11 || |p 12 || |p 13 || |p 14 || |p 15 || |p 16 || |p 17 || |p 18 || Total sime= 5 N 10 |p 3 || [ 10 3|U 1 2 2] [ 10 3| 1 1U 3] |p 4 || [ 10 4| 1 1 4 4] [ 10 4| 2 2 3 3] |p 5 || [ 10 5|U 1 3 3 4 4] [ 10 5| 2 2U 3 4 4] [ 10 5|U 3 3 3 3 3] |p 6 || [ 10 6| 2 2 4 4 4 4] [ 10 6| 3 3 3 3 4 4] |p 7 || [ 10 7|U 1 4 4 4 4 4 4] [ 10 7|U 3 3 3 4 4 4 4] |p 8 || [ 10 8| 3 3 4 4 4 4 4 4] |p 9 || [ 10 9|U 3 4 4 4 4 4 4 4 4] |p 10 || [ 10 10| 4 4 4 4 4 4 4 4 4 4] |p 11 || |p 12 || |p 13 || |p 14 || |p 15 || |p 16 || |p 17 || |p 18 || |p 19 || |p 20 || Total sime= 14 N 11 |p 3 || |p 4 || |p 5 || |p 6 || [ 11 6| 1 1 5 5 5 5] [ 11 6| 2 2 4 4 5 5] [ 11 6| 3 3 3 3 5 5] [ 11 6| 3 3 4 4 4 4] |p 7 || |p 8 || |p 9 || |p 10 || [ 11 10| 2 2 5 5 5 5 5 5 5 5] [ 11 10| 3 3 4 4 5 5 5 5 5 5] [ 11 10| 4 4 4 4 4 4 5 5 5 5] |p 11 || |p 12 || |p 13 || |p 14 || |p 15 || |p 16 || |p 17 || |p 18 || |p 19 || |p 20 || |p 21 || |p 22 || Total sime= 7 N 12 |p 3 || [ 12 3| 1 1U 4] [ 12 3|U 2 2 2] |p 4 || [ 12 4| 1 1 5 5] [ 12 4| 2 2 4 4] [ 12 4| 3 3 3 3] |p 5 || [ 12 5|U 2 3 3 5 5] [ 12 5|U 2 4 4 4 4] [ 12 5| 2 2U 4 5 5] [ 12 5| 3 3U 4 4 4] |p 6 || [ 12 6| 2 2 5 5 5 5] [ 12 6| 3 3 4 4 5 5] [ 12 6| 4 4 4 4 4 4] |p 7 || [ 12 7|U 2 4 4 5 5 5 5] [ 12 7| 3 3U 4 5 5 5 5] [ 12 7|U 4 4 4 4 4 5 5] |p 8 || [ 12 8| 3 3 5 5 5 5 5 5] [ 12 8| 4 4 4 4 5 5 5 5] |p 9 || [ 12 9|U 2 5 5 5 5 5 5 5 5] [ 12 9|U 4 4 4 5 5 5 5 5 5] |p 10 || [ 12 10| 4 4 5 5 5 5 5 5 5 5] |p 11 || [ 12 11|U 4 5 5 5 5 5 5 5 5 5 5] |p 12 || [ 12 12| 5 5 5 5 5 5 5 5 5 5 5 5] |p 13 || |p 14 || |p 15 || |p 16 || |p 17 || |p 18 || |p 19 || |p 20 || |p 21 || |p 22 || |p 23 || |p 24 || Total sime= 22 N 13 |p 3 || |p 4 || |p 5 || |p 6 || [ 13 6| 1 1 6 6 6 6] [ 13 6| 2 2 5 5 6 6] [ 13 6| 3 3 4 4 6 6] [ 13 6| 3 3 5 5 5 5] [ 13 6| 4 4 4 4 5 5] |p 7 || |p 8 || |p 9 || |p 10 || [ 13 10| 2 2 6 6 6 6 6 6 6 6] [ 13 10| 3 3 5 5 6 6 6 6 6 6] [ 13 10| 4 4 4 4 6 6 6 6 6 6] [ 13 10| 4 4 5 5 5 5 6 6 6 6] [ 13 10| 5 5 5 5 5 5 5 5 6 6] |p 11 || |p 12 || |p 13 || |p 14 || |p 15 || |p 16 || |p 17 || |p 18 || |p 19 || |p 20 || |p 21 || |p 22 || |p 23 || |p 24 || |p 25 || |p 26 || Total sime= 10 N 14 |p 3 || [ 14 3|U 1 3 3] [ 14 3| 1 1U 5] [ 14 3| 2 2U 3] |p 4 || [ 14 4| 1 1 6 6] [ 14 4| 2 2 5 5] [ 14 4| 3 3 4 4] |p 5 || [ 14 5|U 1 4 4 6 6] [ 14 5|U 1 5 5 5 5] [ 14 5| 2 2U 5 6 6] [ 14 5|U 3 3 3 6 6] [ 14 5|U 3 4 4 5 5] [ 14 5| 3 3U 5 5 5] [ 14 5| 4 4 4 4U 5] |p 6 || [ 14 6| 2 2 6 6 6 6] [ 14 6| 3 3 5 5 6 6] [ 14 6| 4 4 4 4 6 6] [ 14 6| 4 4 5 5 5 5] |p 7 || [ 14 7|U 1 5 5 6 6 6 6] [ 14 7|U 3 4 4 6 6 6 6] [ 14 7|U 3 5 5 5 5 6 6] [ 14 7| 3 3U 5 6 6 6 6] [ 14 7| 4 4U 5 5 5 6 6] [ 14 7|U 5 5 5 5 5 5 5] |p 8 || [ 14 8| 3 3 6 6 6 6 6 6] [ 14 8| 4 4 5 5 6 6 6 6] [ 14 8| 5 5 5 5 5 5 6 6] |p 9 || [ 14 9|U 1 6 6 6 6 6 6 6 6] [ 14 9|U 3 5 5 6 6 6 6 6 6] [ 14 9| 4 4U 5 6 6 6 6 6 6] [ 14 9|U 5 5 5 5 5 6 6 6 6] |p 10 || [ 14 10| 4 4 6 6 6 6 6 6 6 6] [ 14 10| 5 5 5 5 6 6 6 6 6 6] |p 11 || [ 14 11|U 3 6 6 6 6 6 6 6 6 6 6] [ 14 11|U 5 5 5 6 6 6 6 6 6 6 6] |p 12 || [ 14 12| 5 5 6 6 6 6 6 6 6 6 6 6] |p 13 || |p 14 || |p 15 || |p 16 || |p 17 || |p 18 || |p 19 || |p 20 || |p 21 || |p 22 || |p 23 || |p 24 || |p 25 || |p 26 || |p 27 || |p 28 || Total sime= 35 N 15 |p 3 || |p 4 || |p 5 || |p 6 || [ 15 6| 1 1 7 7 7 7] [ 15 6| 2 2 6 6 7 7] [ 15 6| 3 3 5 5 7 7] [ 15 6| 3 3 6 6 6 6] [ 15 6| 4 4 4 4 7 7] [ 15 6| 4 4 5 5 6 6] [ 15 6| 5 5 5 5 5 5] |p 7 || |p 8 || |p 9 || |p 10 || [ 15 10| 2 2 7 7 7 7 7 7 7 7] [ 15 10| 3 3 6 6 7 7 7 7 7 7] [ 15 10| 4 4 5 5 7 7 7 7 7 7] [ 15 10| 4 4 6 6 6 6 7 7 7 7] [ 15 10| 5 5 5 5 6 6 7 7 7 7] [ 15 10| 5 5 6 6 6 6 6 6 7 7] [ 15 10| 6 6 6 6 6 6 6 6 6 6] |p 11 || |p 12 || |p 13 || |p 14 || |p 15 || |p 16 || |p 17 || |p 18 || |p 19 || |p 20 || |p 21 || |p 22 || |p 23 || |p 24 || |p 25 || |p 26 || |p 27 || |p 28 || |p 29 || |p 30 || Total sime= 14 N 16 p 3 || [ 16 3| 1 1U 6] [ 16 3|U 2 3 3] [ 16 3| 2 2U 4] |p 4 || [ 16 4| 1 1 7 7] [ 16 4| 2 2 6 6] [ 16 4| 3 3 5 5] [ 16 4| 4 4 4 4] |p 5 || [ 16 5|U 2 4 4 7 7] [ 16 5|U 2 5 5 6 6] [ 16 5| 2 2U 6 7 7] [ 16 5| 3 3U 4 7 7] [ 16 5| 3 3U 6 6 6] [ 16 5|U 4 4 4 6 6] [ 16 5|U 4 5 5 5 5] [ 16 5| 4 4 5 5U 6] |p 6 || [ 16 6| 2 2 7 7 7 7] [ 16 6| 3 3 6 6 7 7] [ 16 6| 4 4 5 5 7 7] [ 16 6| 4 4 6 6 6 6] [ 16 6| 5 5 5 5 6 6] |p 7 || [ 16 7|U 2 5 5 7 7 7 7] [ 16 7|U 2 6 6 6 6 7 7] [ 16 7| 3 3U 6 7 7 7 7] [ 16 7|U 4 4 4 7 7 7 7] [ 16 7|U 4 5 5 6 6 7 7] [ 16 7|U 4 6 6 6 6 6 6] [ 16 7| 4 4U 6 6 6 7 7] [ 16 7| 5 5 5 5U 6 7 7] [ 16 7| 5 5U 6 6 6 6 6] |p 8 || [ 16 8| 3 3 7 7 7 7 7 7] [ 16 8| 4 4 6 6 7 7 7 7] [ 16 8| 5 5 5 5 7 7 7 7] [ 16 8| 5 5 6 6 6 6 7 7] [ 16 8| 6 6 6 6 6 6 6 6] |p 9 || [ 16 9|U 2 6 6 7 7 7 7 7 7] [ 16 9|U 4 5 5 7 7 7 7 7 7] [ 16 9|U 4 6 6 6 6 7 7 7 7] [ 16 9| 4 4U 6 7 7 7 7 7 7] [ 16 9| 5 5U 6 6 6 7 7 7 7] [ 16 9|U 6 6 6 6 6 6 6 7 7] |p 10 || [ 16 10| 4 4 7 7 7 7 7 7 7 7] [ 16 10| 5 5 6 6 7 7 7 7 7 7] [ 16 10| 6 6 6 6 6 6 7 7 7 7] |p 11 || [ 16 11|U 2 7 7 7 7 7 7 7 7 7 7] [ 16 11|U 4 6 6 7 7 7 7 7 7 7 7] [ 16 11| 5 5U 6 7 7 7 7 7 7 7 7] [ 16 11|U 6 6 6 6 6 7 7 7 7 7 7] |p 12 || [ 16 12| 5 5 7 7 7 7 7 7 7 7 7 7] [ 16 12| 6 6 6 6 7 7 7 7 7 7 7 7] |p 13 || |p 14 || |p 15 || |p 16 || |p 17 || |p 18 || |p 19 || |p 20 || |p 21 || |p 22 || |p 23 || |p 24 || |p 25 || |p 26 || |p 27 || |p 28 || |p 29 || |p 30 || |p 31 || |p 32 || Total sime= 49 N 17 |p 3 || |p 4 || |p 5 || |p 6 || [ 17 6| 1 1 8 8 8 8] [ 17 6| 2 2 7 7 8 8] [ 17 6| 3 3 6 6 8 8] [ 17 6| 3 3 7 7 7 7] [ 17 6| 4 4 5 5 8 8] [ 17 6| 4 4 6 6 7 7] [ 17 6| 5 5 5 5 7 7] [ 17 6| 5 5 6 6 6 6] |p 7 || |p 8 || |p 9 || |p 10 || [ 17 10| 2 2 8 8 8 8 8 8 8 8] [ 17 10| 3 3 7 7 8 8 8 8 8 8] [ 17 10| 4 4 6 6 8 8 8 8 8 8] [ 17 10| 4 4 7 7 7 7 8 8 8 8] [ 17 10| 5 5 5 5 8 8 8 8 8 8] [ 17 10| 5 5 6 6 7 7 8 8 8 8] [ 17 10| 5 5 7 7 7 7 7 7 8 8] [ 17 10| 6 6 6 6 6 6 8 8 8 8] [ 17 10| 6 6 6 6 7 7 7 7 8 8] [ 17 10| 6 6 7 7 7 7 7 7 7 7] |p 11 || |p 12 || |p 13 || |p 14 || |p 15 || |p 16 || |p 17 || |p 18 || |p 19 || |p 20 || |p 21 || |p 22 || |p 23 || |p 24 || |p 25 || |p 26 || |p 27 || |p 28 || |p 29 || |p 30 || |p 31 || |p 32 || |p 33 || |p 34 || Total sime= 18 N 18 |p 3 || [ 18 3|U 1 4 4] [ 18 3| 1 1U 7] [ 18 3| 2 2U 5] [ 18 3|U 3 3 3] |p 4 || [ 18 4| 1 1 8 8] [ 18 4| 2 2 7 7] [ 18 4| 3 3 6 6] [ 18 4| 4 4 5 5] |p 5 || [ 18 5|U 1 5 5 8 8] [ 18 5|U 1 6 6 7 7] [ 18 5| 2 2U 7 8 8] [ 18 5|U 3 4 4 8 8] [ 18 5|U 3 5 5 7 7] [ 18 5| 3 3U 5 8 8] [ 18 5|U 3 6 6 6 6] [ 18 5| 3 3U 7 7 7] [ 18 5| 4 4U 5 7 7] [ 18 5| 4 4 6 6U 7] [ 18 5|U 5 5 5 6 6] [ 18 5| 5 5 5 5U 7] |p 6 || [ 18 6| 2 2 8 8 8 8] [ 18 6| 3 3 7 7 8 8] [ 18 6| 4 4 6 6 8 8] [ 18 6| 4 4 7 7 7 7] [ 18 6| 5 5 5 5 8 8] [ 18 6| 5 5 6 6 7 7] [ 18 6| 6 6 6 6 6 6] |p 7 || [ 18 7|U 1 6 6 8 8 8 8] [ 18 7|U 1 7 7 7 7 8 8] [ 18 7|U 3 5 5 8 8 8 8] [ 18 7|U 3 6 6 7 7 8 8] [ 18 7|U 3 7 7 7 7 7 7] [ 18 7| 3 3U 7 8 8 8 8] [ 18 7| 4 4U 5 8 8 8 8] [ 18 7| 4 4U 7 7 7 8 8] [ 18 7|U 5 5 5 7 7 8 8] [ 18 7|U 5 6 6 6 6 8 8] [ 18 7|U 5 6 6 7 7 7 7] [ 18 7| 5 5 6 6U 7 8 8] [ 18 7| 5 5U 7 7 7 7 7] [ 18 7| 6 6 6 6U 7 7 7] |p 8 || [ 18 8| 3 3 8 8 8 8 8 8] [ 18 8| 4 4 7 7 8 8 8 8] [ 18 8| 5 5 6 6 8 8 8 8] [ 18 8| 5 5 7 7 7 7 8 8] [ 18 8| 6 6 6 6 7 7 8 8] [ 18 8| 6 6 7 7 7 7 7 7] |p 9 || [ 18 9|U 1 7 7 8 8 8 8 8 8] [ 18 9|U 3 6 6 8 8 8 8 8 8] [ 18 9|U 3 7 7 7 7 8 8 8 8] [ 18 9| 4 4U 7 8 8 8 8 8 8] [ 18 9|U 5 5 5 8 8 8 8 8 8] [ 18 9|U 5 6 6 7 7 8 8 8 8] [ 18 9|U 5 7 7 7 7 7 7 8 8] [ 18 9| 5 5U 7 7 7 8 8 8 8] [ 18 9| 6 6 6 6U 7 8 8 8 8] [ 18 9| 6 6U 7 7 7 7 7 8 8] [ 18 9|U 7 7 7 7 7 7 7 7 7] |p 10 || [ 18 10| 4 4 8 8 8 8 8 8 8 8] [ 18 10| 5 5 7 7 8 8 8 8 8 8] [ 18 10| 6 6 6 6 8 8 8 8 8 8] [ 18 10| 6 6 7 7 7 7 8 8 8 8] [ 18 10| 7 7 7 7 7 7 7 7 8 8] |p 11 || [ 18 11|U 1 8 8 8 8 8 8 8 8 8 8] [ 18 11|U 3 7 7 8 8 8 8 8 8 8 8] [ 18 11|U 5 6 6 8 8 8 8 8 8 8 8] [ 18 11|U 5 7 7 7 7 8 8 8 8 8 8] [ 18 11| 5 5U 7 8 8 8 8 8 8 8 8] [ 18 11| 6 6U 7 7 7 8 8 8 8 8 8] [ 18 11|U 7 7 7 7 7 7 7 8 8 8 8] |p 12 || [ 18 12| 5 5 8 8 8 8 8 8 8 8 8 8] [ 18 12| 6 6 7 7 8 8 8 8 8 8 8 8] [ 18 12| 7 7 7 7 7 7 8 8 8 8 8 8] |p 13 || |p 14 || |p 15 || |p 16 || |p 17 || |p 18 || |p 19 || |p 20 || |p 21 || |p 22 || |p 23 || |p 24 || |p 25 || |p 26 || |p 27 || |p 28 || |p 29 || |p 30 || |p 31 || |p 32 || |p 33 || |p 34 || |p 35 || |p 36 || Total sime= 73 N 19 |p 3 || |p 4 || |p 5 || |p 6 || [ 19 6| 1 1 9 9 9 9] [ 19 6| 2 2 8 8 9 9] [ 19 6| 3 3 7 7 9 9] [ 19 6| 3 3 8 8 8 8] [ 19 6| 4 4 6 6 9 9] [ 19 6| 4 4 7 7 8 8] [ 19 6| 5 5 5 5 9 9] [ 19 6| 5 5 6 6 8 8] [ 19 6| 5 5 7 7 7 7] [ 19 6| 6 6 6 6 7 7] |p 7 || |p 8 || |p 9 || |p 10 || [ 19 10| 2 2 9 9 9 9 9 9 9 9] [ 19 10| 3 3 8 8 9 9 9 9 9 9] [ 19 10| 4 4 7 7 9 9 9 9 9 9] [ 19 10| 4 4 8 8 8 8 9 9 9 9] [ 19 10| 5 5 6 6 9 9 9 9 9 9] [ 19 10| 5 5 7 7 8 8 9 9 9 9] [ 19 10| 5 5 8 8 8 8 8 8 9 9] [ 19 10| 6 6 6 6 8 8 9 9 9 9] [ 19 10| 6 6 7 7 7 7 9 9 9 9] [ 19 10| 6 6 7 7 8 8 8 8 9 9] [ 19 10| 6 6 8 8 8 8 8 8 8 8] [ 19 10| 7 7 7 7 7 7 8 8 9 9] [ 19 10| 7 7 7 7 8 8 8 8 8 8] |p 11 || |p 12 || |p 13 || |p 14 || |p 15 || |p 16 || |p 17 || |p 18 || |p 19 || |p 20 || |p 21 || |p 22 || |p 23 || |p 24 || |p 25 || |p 26 || |p 27 || |p 28 || |p 29 || |p 30 || |p 31 || |p 32 || |p 33 || |p 34 || |p 35 || |p 36 || |p 37 || |p 38 || Total sime= 23 N 20 |p 3 || [ 20 3| 1 1U 8] [ 20 3|U 2 4 4] [ 20 3| 2 2U 6] [ 20 3| 3 3U 4] |p 4 || [ 20 4| 1 1 9 9] [ 20 4| 2 2 8 8] [ 20 4| 3 3 7 7] [ 20 4| 4 4 6 6] [ 20 4| 5 5 5 5] |p 5 || [ 20 5|U 2 5 5 9 9] [ 20 5|U 2 6 6 8 8] [ 20 5|U 2 7 7 7 7] [ 20 5| 2 2U 8 9 9] [ 20 5| 3 3U 6 9 9] [ 20 5| 3 3U 8 8 8] [ 20 5|U 4 4 4 9 9] [ 20 5|U 4 5 5 8 8] [ 20 5|U 4 6 6 7 7] [ 20 5| 4 4U 6 8 8] [ 20 5| 4 4 7 7U 8] [ 20 5| 5 5U 6 7 7] [ 20 5| 5 5 6 6U 8] [ 20 5|U 6 6 6 6 6] |p 6 || [ 20 6| 2 2 9 9 9 9] [ 20 6| 3 3 8 8 9 9] [ 20 6| 4 4 7 7 9 9] [ 20 6| 4 4 8 8 8 8] [ 20 6| 5 5 6 6 9 9] [ 20 6| 5 5 7 7 8 8] [ 20 6| 6 6 6 6 8 8] [ 20 6| 6 6 7 7 7 7] |p 7 || [ 20 7|U 2 6 6 9 9 9 9] [ 20 7|U 2 7 7 8 8 9 9] [ 20 7|U 2 8 8 8 8 8 8] [ 20 7| 3 3U 8 9 9 9 9] [ 20 7|U 4 5 5 9 9 9 9] [ 20 7|U 4 6 6 8 8 9 9] [ 20 7| 4 4U 6 9 9 9 9] [ 20 7|U 4 7 7 7 7 9 9] [ 20 7|U 4 7 7 8 8 8 8] [ 20 7| 4 4U 8 8 8 9 9] [ 20 7| 5 5U 6 8 8 9 9] [ 20 7| 5 5 7 7U 8 9 9] [ 20 7| 5 5U 8 8 8 8 8] [ 20 7|U 6 6 6 7 7 9 9] [ 20 7|U 6 6 6 8 8 8 8] [ 20 7| 6 6 6 6U 8 9 9] [ 20 7|U 6 7 7 7 7 8 8] [ 20 7| 6 6 7 7U 8 8 8] [ 20 7| 7 7 7 7 7 7U 8] |p 8 || [ 20 8| 3 3 9 9 9 9 9 9] [ 20 8| 4 4 8 8 9 9 9 9] [ 20 8| 5 5 7 7 9 9 9 9] [ 20 8| 5 5 8 8 8 8 9 9] [ 20 8| 6 6 6 6 9 9 9 9] [ 20 8| 6 6 7 7 8 8 9 9] [ 20 8| 6 6 8 8 8 8 8 8] [ 20 8| 7 7 7 7 7 7 9 9] [ 20 8| 7 7 7 7 8 8 8 8] |p 9 || [ 20 9|U 2 7 7 9 9 9 9 9 9] [ 20 9|U 2 8 8 8 8 9 9 9 9] [ 20 9|U 4 6 6 9 9 9 9 9 9] [ 20 9|U 4 7 7 8 8 9 9 9 9] [ 20 9|U 4 8 8 8 8 8 8 9 9] [ 20 9| 4 4U 8 9 9 9 9 9 9] [ 20 9| 5 5U 6 9 9 9 9 9 9] [ 20 9| 5 5U 8 8 8 9 9 9 9] [ 20 9|U 6 6 6 8 8 9 9 9 9] [ 20 9|U 6 7 7 7 7 9 9 9 9] [ 20 9|U 6 7 7 8 8 8 8 9 9] [ 20 9| 6 6 7 7U 8 9 9 9 9] [ 20 9|U 6 8 8 8 8 8 8 8 8] [ 20 9| 6 6U 8 8 8 8 8 9 9] [ 20 9| 7 7 7 7U 8 8 8 9 9] [ 20 9| 7 7U 8 8 8 8 8 8 8] |p 10 || [ 20 10| 4 4 9 9 9 9 9 9 9 9] [ 20 10| 5 5 8 8 9 9 9 9 9 9] [ 20 10| 6 6 7 7 9 9 9 9 9 9] [ 20 10| 6 6 8 8 8 8 9 9 9 9] [ 20 10| 7 7 7 7 8 8 9 9 9 9] [ 20 10| 7 7 8 8 8 8 8 8 9 9] [ 20 10| 8 8 8 8 8 8 8 8 8 8] |p 11 || [ 20 11|U 2 8 8 9 9 9 9 9 9 9 9] [ 20 11|U 4 7 7 9 9 9 9 9 9 9 9] [ 20 11|U 4 8 8 8 8 9 9 9 9 9 9] [ 20 11| 5 5U 8 9 9 9 9 9 9 9 9] [ 20 11|U 6 6 6 9 9 9 9 9 9 9 9] [ 20 11|U 6 7 7 8 8 9 9 9 9 9 9] [ 20 11|U 6 8 8 8 8 8 8 9 9 9 9] [ 20 11| 6 6U 8 8 8 9 9 9 9 9 9] [ 20 11| 7 7 7 7U 8 9 9 9 9 9 9] [ 20 11| 7 7U 8 8 8 8 8 9 9 9 9] [ 20 11|U 8 8 8 8 8 8 8 8 8 9 9] |p 12 || [ 20 12| 5 5 9 9 9 9 9 9 9 9 9 9] [ 20 12| 6 6 8 8 9 9 9 9 9 9 9 9] [ 20 12| 7 7 7 7 9 9 9 9 9 9 9 9] [ 20 12| 7 7 8 8 8 8 9 9 9 9 9 9] [ 20 12| 8 8 8 8 8 8 8 8 9 9 9 9] |p 13 || |p 14 || |p 15 || |p 16 || |p 17 || |p 18 || |p 19 || |p 20 || |p 21 || |p 22 || |p 23 || |p 24 || |p 25 || |p 26 || |p 27 || |p 28 || |p 29 || |p 30 || |p 31 || |p 32 || |p 33 || |p 34 || |p 35 || |p 36 || |p 37 || |p 38 || |p 39 || |p 40 || Total sime= 98 N 21 |p 3 || |p 4 || |p 5 || |p 6 || [ 21 6| 1 1 10 10 10 10] [ 21 6| 2 2 9 9 10 10] [ 21 6| 3 3 8 8 10 10] [ 21 6| 3 3 9 9 9 9] [ 21 6| 4 4 7 7 10 10] [ 21 6| 4 4 8 8 9 9] [ 21 6| 5 5 6 6 10 10] [ 21 6| 5 5 7 7 9 9] [ 21 6| 5 5 8 8 8 8] [ 21 6| 6 6 6 6 9 9] [ 21 6| 6 6 7 7 8 8] [ 21 6| 7 7 7 7 7 7] |p 7 || |p 8 || |p 9 || |p 10 || [ 21 10| 2 2 10 10 10 10 10 10 10 10] [ 21 10| 3 3 9 9 10 10 10 10 10 10] [ 21 10| 4 4 8 8 10 10 10 10 10 10] [ 21 10| 4 4 9 9 9 9 10 10 10 10] [ 21 10| 5 5 7 7 10 10 10 10 10 10] [ 21 10| 5 5 8 8 9 9 10 10 10 10] [ 21 10| 5 5 9 9 9 9 9 9 10 10] [ 21 10| 6 6 6 6 10 10 10 10 10 10] [ 21 10| 6 6 7 7 9 9 10 10 10 10] [ 21 10| 6 6 8 8 8 8 10 10 10 10] [ 21 10| 6 6 8 8 9 9 9 9 10 10] [ 21 10| 6 6 9 9 9 9 9 9 9 9] [ 21 10| 7 7 7 7 8 8 10 10 10 10] [ 21 10| 7 7 7 7 9 9 9 9 10 10] [ 21 10| 7 7 8 8 8 8 9 9 10 10] [ 21 10| 7 7 8 8 9 9 9 9 9 9] [ 21 10| 8 8 8 8 8 8 8 8 10 10] [ 21 10| 8 8 8 8 8 8 9 9 9 9] |p 11 || |p 12 || |p 13 || |p 14 || |p 15 || |p 16 || |p 17 || |p 18 || |p 19 || |p 20 || |p 21 || |p 22 || |p 23 || |p 24 || |p 25 || |p 26 || |p 27 || |p 28 || |p 29 || |p 30 || |p 31 || |p 32 || |p 33 || |p 34 || |p 35 || |p 36 || |p 37 || |p 38 || |p 39 || |p 40 || |p 41 || |p 42 || Total sime= 30 N 22 |p 3 || [ 22 3|U 1 5 5] [ 22 3| 1 1U 9] [ 22 3| 2 2U 7] [ 22 3|U 3 4 4] [ 22 3| 3 3U 5] |p 4 || [ 22 4| 1 1 10 10] [ 22 4| 2 2 9 9] [ 22 4| 3 3 8 8] [ 22 4| 4 4 7 7] [ 22 4| 5 5 6 6] |p 5 || [ 22 5|U 1 6 6 10 10] [ 22 5|U 1 7 7 9 9] [ 22 5|U 1 8 8 8 8] [ 22 5| 2 2U 9 10 10] [ 22 5|U 3 5 5 10 10] [ 22 5|U 3 6 6 9 9] [ 22 5|U 3 7 7 8 8] [ 22 5| 3 3U 7 10 10] [ 22 5| 3 3U 9 9 9] [ 22 5| 4 4U 5 10 10] [ 22 5| 4 4U 7 9 9] [ 22 5| 4 4 8 8U 9] [ 22 5|U 5 5 5 9 9] [ 22 5|U 5 6 6 8 8] [ 22 5|U 5 7 7 7 7] [ 22 5| 5 5U 7 8 8] [ 22 5| 5 5 7 7U 9] [ 22 5| 6 6 6 6U 9] [ 22 5| 6 6U 7 7 7] |p 6 || [ 22 6| 2 2 10 10 10 10] [ 22 6| 3 3 9 9 10 10] [ 22 6| 4 4 8 8 10 10] [ 22 6| 4 4 9 9 9 9] [ 22 6| 5 5 7 7 10 10] [ 22 6| 5 5 8 8 9 9] [ 22 6| 6 6 6 6 10 10] [ 22 6| 6 6 7 7 9 9] [ 22 6| 6 6 8 8 8 8] [ 22 6| 7 7 7 7 8 8] |p 7 || [ 22 7|U 1 7 7 10 10 10 10] [ 22 7|U 1 8 8 9 9 10 10] [ 22 7|U 1 9 9 9 9 9 9] [ 22 7|U 3 6 6 10 10 10 10] [ 22 7|U 3 7 7 9 9 10 10] [ 22 7|U 3 8 8 8 8 10 10] [ 22 7|U 3 8 8 9 9 9 9] [ 22 7| 3 3U 9 10 10 10 10] [ 22 7| 4 4U 7 10 10 10 10] [ 22 7| 4 4U 9 9 9 10 10] [ 22 7|U 5 5 5 10 10 10 10] [ 22 7|U 5 6 6 9 9 10 10] [ 22 7|U 5 7 7 8 8 10 10] [ 22 7|U 5 7 7 9 9 9 9] [ 22 7| 5 5U 7 9 9 10 10] [ 22 7|U 5 8 8 8 8 9 9] [ 22 7| 5 5 8 8U 9 10 10] [ 22 7| 5 5U 9 9 9 9 9] [ 22 7| 6 6U 7 8 8 10 10] [ 22 7| 6 6U 7 9 9 9 9] [ 22 7| 6 6 7 7U 9 10 10] [ 22 7| 6 6 8 8U 9 9 9] [ 22 7|U 7 7 7 7 7 10 10] [ 22 7|U 7 7 7 8 8 9 9] [ 22 7| 7 7 7 7U 9 9 9] [ 22 7|U 7 8 8 8 8 8 8] [ 22 7| 7 7 8 8 8 8U 9] |p 8 || [ 22 8| 3 3 10 10 10 10 10 10] [ 22 8| 4 4 9 9 10 10 10 10] [ 22 8| 5 5 8 8 10 10 10 10] [ 22 8| 5 5 9 9 9 9 10 10] [ 22 8| 6 6 7 7 10 10 10 10] [ 22 8| 6 6 8 8 9 9 10 10] [ 22 8| 6 6 9 9 9 9 9 9] [ 22 8| 7 7 7 7 9 9 10 10] [ 22 8| 7 7 8 8 8 8 10 10] [ 22 8| 7 7 8 8 9 9 9 9] [ 22 8| 8 8 8 8 8 8 9 9] |p 9 || [ 22 9|U 1 8 8 10 10 10 10 10 10] [ 22 9|U 1 9 9 9 9 10 10 10 10] [ 22 9|U 3 7 7 10 10 10 10 10 10] [ 22 9|U 3 8 8 9 9 10 10 10 10] [ 22 9|U 3 9 9 9 9 9 9 10 10] [ 22 9| 4 4U 9 10 10 10 10 10 10] [ 22 9|U 5 6 6 10 10 10 10 10 10] [ 22 9|U 5 7 7 9 9 10 10 10 10] [ 22 9| 5 5U 7 10 10 10 10 10 10] [ 22 9|U 5 8 8 8 8 10 10 10 10] [ 22 9|U 5 8 8 9 9 9 9 10 10] [ 22 9|U 5 9 9 9 9 9 9 9 9] [ 22 9| 5 5U 9 9 9 10 10 10 10] [ 22 9| 6 6U 7 9 9 10 10 10 10] [ 22 9| 6 6 8 8U 9 10 10 10 10] [ 22 9| 6 6U 9 9 9 9 9 10 10] [ 22 9|U 7 7 7 8 8 10 10 10 10] [ 22 9|U 7 7 7 9 9 9 9 10 10] [ 22 9| 7 7 7 7U 9 10 10 10 10] [ 22 9|U 7 8 8 8 8 9 9 10 10] [ 22 9|U 7 8 8 9 9 9 9 9 9] [ 22 9| 7 7 8 8U 9 9 9 10 10] [ 22 9| 7 7U 9 9 9 9 9 9 9] [ 22 9| 8 8 8 8 8 8U 9 10 10] [ 22 9| 8 8 8 8U 9 9 9 9 9] |p 10 || [ 22 10| 4 4 10 10 10 10 10 10 10 10] [ 22 10| 5 5 9 9 10 10 10 10 10 10] [ 22 10| 6 6 8 8 10 10 10 10 10 10] [ 22 10| 6 6 9 9 9 9 10 10 10 10] [ 22 10| 7 7 7 7 10 10 10 10 10 10] [ 22 10| 7 7 8 8 9 9 10 10 10 10] [ 22 10| 7 7 9 9 9 9 9 9 10 10] [ 22 10| 8 8 8 8 8 8 10 10 10 10] [ 22 10| 8 8 8 8 9 9 9 9 10 10] [ 22 10| 8 8 9 9 9 9 9 9 9 9] |p 11 || [ 22 11|U 1 9 9 10 10 10 10 10 10 10 10] [ 22 11|U 3 8 8 10 10 10 10 10 10 10 10] [ 22 11|U 3 9 9 9 9 10 10 10 10 10 10] [ 22 11|U 5 7 7 10 10 10 10 10 10 10 10] [ 22 11|U 5 8 8 9 9 10 10 10 10 10 10] [ 22 11|U 5 9 9 9 9 9 9 10 10 10 10] [ 22 11| 5 5U 9 10 10 10 10 10 10 10 10] [ 22 11| 6 6U 7 10 10 10 10 10 10 10 10] [ 22 11| 6 6U 9 9 9 10 10 10 10 10 10] [ 22 11|U 7 7 7 9 9 10 10 10 10 10 10] [ 22 11|U 7 8 8 8 8 10 10 10 10 10 10] [ 22 11|U 7 8 8 9 9 9 9 10 10 10 10] [ 22 11| 7 7 8 8U 9 10 10 10 10 10 10] [ 22 11|U 7 9 9 9 9 9 9 9 9 10 10] [ 22 11| 7 7U 9 9 9 9 9 10 10 10 10] [ 22 11| 8 8 8 8U 9 9 9 10 10 10 10] [ 22 11| 8 8U 9 9 9 9 9 9 9 10 10] [ 22 11|U 9 9 9 9 9 9 9 9 9 9 9] |p 12 || [ 22 12| 5 5 10 10 10 10 10 10 10 10 10 10] [ 22 12| 6 6 9 9 10 10 10 10 10 10 10 10] [ 22 12| 7 7 8 8 10 10 10 10 10 10 10 10] [ 22 12| 7 7 9 9 9 9 10 10 10 10 10 10] [ 22 12| 8 8 8 8 9 9 10 10 10 10 10 10] [ 22 12| 8 8 9 9 9 9 9 9 10 10 10 10] [ 22 12| 9 9 9 9 9 9 9 9 9 9 10 10] |p 13 || |p 14 || |p 15 || |p 16 || |p 17 || |p 18 || |p 19 || |p 20 || |p 21 || |p 22 || |p 23 || |p 24 || |p 25 || |p 26 || |p 27 || |p 28 || |p 29 || |p 30 || |p 31 || |p 32 || |p 33 || |p 34 || |p 35 || |p 36 || |p 37 || |p 38 || |p 39 || |p 40 || |p 41 || |p 42 || |p 43 || |p 44 || Total sime= 137 N 23 |p 3 || |p 4 || |p 5 || |p 6 || [ 23 6| 1 1 11 11 11 11] [ 23 6| 2 2 10 10 11 11] [ 23 6| 3 3 9 9 11 11] [ 23 6| 3 3 10 10 10 10] [ 23 6| 4 4 8 8 11 11] [ 23 6| 4 4 9 9 10 10] [ 23 6| 5 5 7 7 11 11] [ 23 6| 5 5 8 8 10 10] [ 23 6| 5 5 9 9 9 9] [ 23 6| 6 6 6 6 11 11] [ 23 6| 6 6 7 7 10 10] [ 23 6| 6 6 8 8 9 9] [ 23 6| 7 7 7 7 9 9] [ 23 6| 7 7 8 8 8 8] |p 7 || |p 8 || |p 9 || |p 10 || [ 23 10| 2 2 11 11 11 11 11 11 11 11] [ 23 10| 3 3 10 10 11 11 11 11 11 11] [ 23 10| 4 4 9 9 11 11 11 11 11 11] [ 23 10| 4 4 10 10 10 10 11 11 11 11] [ 23 10| 5 5 8 8 11 11 11 11 11 11] [ 23 10| 5 5 9 9 10 10 11 11 11 11] [ 23 10| 5 5 10 10 10 10 10 10 11 11] [ 23 10| 6 6 7 7 11 11 11 11 11 11] [ 23 10| 6 6 8 8 10 10 11 11 11 11] [ 23 10| 6 6 9 9 9 9 11 11 11 11] [ 23 10| 6 6 9 9 10 10 10 10 11 11] [ 23 10| 6 6 10 10 10 10 10 10 10 10] [ 23 10| 7 7 7 7 10 10 11 11 11 11] [ 23 10| 7 7 8 8 9 9 11 11 11 11] [ 23 10| 7 7 8 8 10 10 10 10 11 11] [ 23 10| 7 7 9 9 9 9 10 10 11 11] [ 23 10| 7 7 9 9 10 10 10 10 10 10] [ 23 10| 8 8 8 8 8 8 11 11 11 11] [ 23 10| 8 8 8 8 9 9 10 10 11 11] [ 23 10| 8 8 8 8 10 10 10 10 10 10] [ 23 10| 8 8 9 9 9 9 9 9 11 11] [ 23 10| 8 8 9 9 9 9 10 10 10 10] [ 23 10| 9 9 9 9 9 9 9 9 10 10] |p 11 || |p 12 || |p 13 || |p 14 || |p 15 || |p 16 || |p 17 || |p 18 || |p 19 || |p 20 || |p 21 || |p 22 || |p 23 || |p 24 || |p 25 || |p 26 || |p 27 || |p 28 || |p 29 || |p 30 || |p 31 || |p 32 || |p 33 || |p 34 || |p 35 || |p 36 || |p 37 || |p 38 || |p 39 || |p 40 || |p 41 || |p 42 || |p 43 || |p 44 || |p 45 || |p 46 || Total sime= 37 N 24 |p 3 || [ 24 3| 1 1U 10] [ 24 3|U 2 5 5] [ 24 3| 2 2U 8] [ 24 3| 3 3U 6] [ 24 3|U 4 4 4] |p 4 || [ 24 4| 1 1 11 11] [ 24 4| 2 2 10 10] [ 24 4| 3 3 9 9] [ 24 4| 4 4 8 8] [ 24 4| 5 5 7 7] [ 24 4| 6 6 6 6] |p 5 || [ 24 5|U 2 6 6 11 11] [ 24 5|U 2 7 7 10 10] [ 24 5|U 2 8 8 9 9] [ 24 5| 2 2U 10 11 11] [ 24 5| 3 3U 8 11 11] [ 24 5| 3 3U 10 10 10] [ 24 5|U 4 5 5 11 11] [ 24 5|U 4 6 6 10 10] [ 24 5| 4 4U 6 11 11] [ 24 5|U 4 7 7 9 9] [ 24 5|U 4 8 8 8 8] [ 24 5| 4 4U 8 10 10] [ 24 5| 4 4 9 9U 10] [ 24 5| 5 5U 6 10 10] [ 24 5| 5 5U 8 9 9] [ 24 5| 5 5 8 8U 10] [ 24 5|U 6 6 6 9 9] [ 24 5|U 6 7 7 8 8] [ 24 5| 6 6 7 7U 10] [ 24 5| 6 6U 8 8 8] [ 24 5| 7 7 7 7U 8] |p 6 || [ 24 6| 2 2 11 11 11 11] [ 24 6| 3 3 10 10 11 11] [ 24 6| 4 4 9 9 11 11] [ 24 6| 4 4 10 10 10 10] [ 24 6| 5 5 8 8 11 11] [ 24 6| 5 5 9 9 10 10] [ 24 6| 6 6 7 7 11 11] [ 24 6| 6 6 8 8 10 10] [ 24 6| 6 6 9 9 9 9] [ 24 6| 7 7 7 7 10 10] [ 24 6| 7 7 8 8 9 9] [ 24 6| 8 8 8 8 8 8] |p 7 || [ 24 7|U 2 7 7 11 11 11 11] [ 24 7|U 2 8 8 10 10 11 11] [ 24 7|U 2 9 9 9 9 11 11] [ 24 7|U 2 9 9 10 10 10 10] [ 24 7| 3 3U 10 11 11 11 11] [ 24 7|U 4 6 6 11 11 11 11] [ 24 7|U 4 7 7 10 10 11 11] [ 24 7|U 4 8 8 9 9 11 11] [ 24 7|U 4 8 8 10 10 10 10] [ 24 7| 4 4U 8 11 11 11 11] [ 24 7|U 4 9 9 9 9 10 10] [ 24 7| 4 4U 10 10 10 11 11] [ 24 7| 5 5U 6 11 11 11 11] [ 24 7| 5 5U 8 10 10 11 11] [ 24 7| 5 5 9 9U 10 11 11] [ 24 7| 5 5U 10 10 10 10 10] [ 24 7|U 6 6 6 10 10 11 11] [ 24 7|U 6 7 7 9 9 11 11] [ 24 7|U 6 7 7 10 10 10 10] [ 24 7|U 6 8 8 8 8 11 11] [ 24 7|U 6 8 8 9 9 10 10] [ 24 7| 6 6U 8 9 9 11 11] [ 24 7| 6 6U 8 10 10 10 10] [ 24 7| 6 6 8 8U 10 11 11] [ 24 7|U 6 9 9 9 9 9 9] [ 24 7| 6 6 9 9U 10 10 10] [ 24 7| 7 7 7 7U 10 11 11] [ 24 7| 7 7U 8 8 8 11 11] [ 24 7| 7 7U 8 9 9 10 10] [ 24 7| 7 7 8 8U 10 10 10] [ 24 7| 7 7 9 9 9 9U 10] [ 24 7|U 8 8 8 8 8 10 10] [ 24 7|U 8 8 8 9 9 9 9] [ 24 7| 8 8 8 8 9 9U 10] |p 8 || [ 24 8| 3 3 11 11 11 11 11 11] [ 24 8| 4 4 10 10 11 11 11 11] [ 24 8| 5 5 9 9 11 11 11 11] [ 24 8| 5 5 10 10 10 10 11 11] [ 24 8| 6 6 8 8 11 11 11 11] [ 24 8| 6 6 9 9 10 10 11 11] [ 24 8| 6 6 10 10 10 10 10 10] [ 24 8| 7 7 7 7 11 11 11 11] [ 24 8| 7 7 8 8 10 10 11 11] [ 24 8| 7 7 9 9 9 9 11 11] [ 24 8| 7 7 9 9 10 10 10 10] [ 24 8| 8 8 8 8 9 9 11 11] [ 24 8| 8 8 8 8 10 10 10 10] [ 24 8| 8 8 9 9 9 9 10 10] [ 24 8| 9 9 9 9 9 9 9 9] |p 9 || [ 24 9|U 2 8 8 11 11 11 11 11 11] [ 24 9|U 2 9 9 10 10 11 11 11 11] [ 24 9|U 2 10 10 10 10 10 10 11 11] [ 24 9|U 4 7 7 11 11 11 11 11 11] [ 24 9|U 4 8 8 10 10 11 11 11 11] [ 24 9|U 4 9 9 9 9 11 11 11 11] [ 24 9|U 4 9 9 10 10 10 10 11 11] [ 24 9|U 4 10 10 10 10 10 10 10 10] [ 24 9| 4 4U 10 11 11 11 11 11 11] [ 24 9| 5 5U 8 11 11 11 11 11 11] [ 24 9| 5 5U 10 10 10 11 11 11 11] [ 24 9|U 6 6 6 11 11 11 11 11 11] [ 24 9|U 6 7 7 10 10 11 11 11 11] [ 24 9|U 6 8 8 9 9 11 11 11 11] [ 24 9|U 6 8 8 10 10 10 10 11 11] [ 24 9| 6 6U 8 10 10 11 11 11 11] [ 24 9|U 6 9 9 9 9 10 10 11 11] [ 24 9|U 6 9 9 10 10 10 10 10 10] [ 24 9| 6 6 9 9U 10 11 11 11 11] [ 24 9| 6 6U 10 10 10 10 10 11 11] [ 24 9| 7 7U 8 9 9 11 11 11 11] [ 24 9| 7 7U 8 10 10 10 10 11 11] [ 24 9| 7 7 8 8U 10 11 11 11 11] [ 24 9| 7 7 9 9U 10 10 10 11 11] [ 24 9| 7 7U 10 10 10 10 10 10 10] [ 24 9|U 8 8 8 8 8 11 11 11 11] [ 24 9|U 8 8 8 9 9 10 10 11 11] [ 24 9|U 8 8 8 10 10 10 10 10 10] [ 24 9| 8 8 8 8U 10 10 10 11 11] [ 24 9|U 8 9 9 9 9 9 9 11 11] [ 24 9|U 8 9 9 9 9 10 10 10 10] [ 24 9| 8 8 9 9 9 9U 10 11 11] [ 24 9| 8 8 9 9U 10 10 10 10 10] [ 24 9| 9 9 9 9 9 9U 10 10 10] |p 10 || [ 24 10| 4 4 11 11 11 11 11 11 11 11] [ 24 10| 5 5 10 10 11 11 11 11 11 11] [ 24 10| 6 6 9 9 11 11 11 11 11 11] [ 24 10| 6 6 10 10 10 10 11 11 11 11] [ 24 10| 7 7 8 8 11 11 11 11 11 11] [ 24 10| 7 7 9 9 10 10 11 11 11 11] [ 24 10| 7 7 10 10 10 10 10 10 11 11] [ 24 10| 8 8 8 8 10 10 11 11 11 11] [ 24 10| 8 8 9 9 9 9 11 11 11 11] [ 24 10| 8 8 9 9 10 10 10 10 11 11] [ 24 10| 8 8 10 10 10 10 10 10 10 10] [ 24 10| 9 9 9 9 9 9 10 10 11 11] [ 24 10| 9 9 9 9 10 10 10 10 10 10] |p 11 || [ 24 11|U 2 9 9 11 11 11 11 11 11 11 11] [ 24 11|U 2 10 10 10 10 11 11 11 11 11 11] [ 24 11|U 4 8 8 11 11 11 11 11 11 11 11] [ 24 11|U 4 9 9 10 10 11 11 11 11 11 11] [ 24 11|U 4 10 10 10 10 10 10 11 11 11 11] [ 24 11| 5 5U 10 11 11 11 11 11 11 11 11] [ 24 11|U 6 7 7 11 11 11 11 11 11 11 11] [ 24 11|U 6 8 8 10 10 11 11 11 11 11 11] [ 24 11| 6 6U 8 11 11 11 11 11 11 11 11] [ 24 11|U 6 9 9 9 9 11 11 11 11 11 11] [ 24 11|U 6 9 9 10 10 10 10 11 11 11 11] [ 24 11|U 6 10 10 10 10 10 10 10 10 11 11] [ 24 11| 6 6U 10 10 10 11 11 11 11 11 11] [ 24 11| 7 7U 8 10 10 11 11 11 11 11 11] [ 24 11| 7 7 9 9U 10 11 11 11 11 11 11] [ 24 11| 7 7U 10 10 10 10 10 11 11 11 11] [ 24 11|U 8 8 8 9 9 11 11 11 11 11 11] [ 24 11|U 8 8 8 10 10 10 10 11 11 11 11] [ 24 11| 8 8 8 8U 10 11 11 11 11 11 11] [ 24 11|U 8 9 9 9 9 10 10 11 11 11 11] [ 24 11|U 8 9 9 10 10 10 10 10 10 11 11] [ 24 11| 8 8 9 9U 10 10 10 11 11 11 11] [ 24 11|U 8 10 10 10 10 10 10 10 10 10 10] [ 24 11| 8 8U 10 10 10 10 10 10 10 11 11] [ 24 11| 9 9 9 9 9 9U 10 11 11 11 11] [ 24 11| 9 9 9 9U 10 10 10 10 10 11 11] [ 24 11| 9 9U 10 10 10 10 10 10 10 10 10] |p 12 || [ 24 12| 5 5 11 11 11 11 11 11 11 11 11 11] [ 24 12| 6 6 10 10 11 11 11 11 11 11 11 11] [ 24 12| 7 7 9 9 11 11 11 11 11 11 11 11] [ 24 12| 7 7 10 10 10 10 11 11 11 11 11 11] [ 24 12| 8 8 8 8 11 11 11 11 11 11 11 11] [ 24 12| 8 8 9 9 10 10 11 11 11 11 11 11] [ 24 12| 8 8 10 10 10 10 10 10 11 11 11 11] [ 24 12| 9 9 9 9 9 9 11 11 11 11 11 11] [ 24 12| 9 9 9 9 10 10 10 10 11 11 11 11] [ 24 12| 9 9 10 10 10 10 10 10 10 10 11 11] [ 24 12| 10 10 10 10 10 10 10 10 10 10 10 10] |p 13 || |p 14 || |p 15 || |p 16 || |p 17 || |p 18 || |p 19 || |p 20 || |p 21 || |p 22 || |p 23 || |p 24 || |p 25 || |p 26 || |p 27 || |p 28 || |p 29 || |p 30 || |p 31 || |p 32 || |p 33 || |p 34 || |p 35 || |p 36 || |p 37 || |p 38 || |p 39 || |p 40 || |p 41 || |p 42 || |p 43 || |p 44 || |p 45 || |p 46 || |p 47 || |p 48 || Total sime= 178 N 25 |p 3 || |p 4 || |p 5 || |p 6 || [ 25 6| 1 1 12 12 12 12] [ 25 6| 2 2 11 11 12 12] [ 25 6| 3 3 10 10 12 12] [ 25 6| 3 3 11 11 11 11] [ 25 6| 4 4 9 9 12 12] [ 25 6| 4 4 10 10 11 11] [ 25 6| 5 5 8 8 12 12] [ 25 6| 5 5 9 9 11 11] [ 25 6| 5 5 10 10 10 10] [ 25 6| 6 6 7 7 12 12] [ 25 6| 6 6 8 8 11 11] [ 25 6| 6 6 9 9 10 10] [ 25 6| 7 7 7 7 11 11] [ 25 6| 7 7 8 8 10 10] [ 25 6| 7 7 9 9 9 9] [ 25 6| 8 8 8 8 9 9] |p 7 || |p 8 || |p 9 || |p 10 || [ 25 10| 2 2 12 12 12 12 12 12 12 12] [ 25 10| 3 3 11 11 12 12 12 12 12 12] [ 25 10| 4 4 10 10 12 12 12 12 12 12] [ 25 10| 4 4 11 11 11 11 12 12 12 12] [ 25 10| 5 5 9 9 12 12 12 12 12 12] [ 25 10| 5 5 10 10 11 11 12 12 12 12] [ 25 10| 5 5 11 11 11 11 11 11 12 12] [ 25 10| 6 6 8 8 12 12 12 12 12 12] [ 25 10| 6 6 9 9 11 11 12 12 12 12] [ 25 10| 6 6 10 10 10 10 12 12 12 12] [ 25 10| 6 6 10 10 11 11 11 11 12 12] [ 25 10| 6 6 11 11 11 11 11 11 11 11] [ 25 10| 7 7 7 7 12 12 12 12 12 12] [ 25 10| 7 7 8 8 11 11 12 12 12 12] [ 25 10| 7 7 9 9 10 10 12 12 12 12] [ 25 10| 7 7 9 9 11 11 11 11 12 12] [ 25 10| 7 7 10 10 10 10 11 11 12 12] [ 25 10| 7 7 10 10 11 11 11 11 11 11] [ 25 10| 8 8 8 8 10 10 12 12 12 12] [ 25 10| 8 8 8 8 11 11 11 11 12 12] [ 25 10| 8 8 9 9 9 9 12 12 12 12] [ 25 10| 8 8 9 9 10 10 11 11 12 12] [ 25 10| 8 8 9 9 11 11 11 11 11 11] [ 25 10| 8 8 10 10 10 10 10 10 12 12] [ 25 10| 8 8 10 10 10 10 11 11 11 11] [ 25 10| 9 9 9 9 9 9 11 11 12 12] [ 25 10| 9 9 9 9 10 10 10 10 12 12] [ 25 10| 9 9 9 9 10 10 11 11 11 11] [ 25 10| 9 9 10 10 10 10 10 10 11 11] [ 25 10| 10 10 10 10 10 10 10 10 10 10] |p 11 || |p 12 || |p 13 || |p 14 || |p 15 || |p 16 || |p 17 || |p 18 || |p 19 || |p 20 || |p 21 || |p 22 || |p 23 || |p 24 || |p 25 || |p 26 || |p 27 || |p 28 || |p 29 || |p 30 || |p 31 || |p 32 || |p 33 || |p 34 || |p 35 || |p 36 || |p 37 || |p 38 || |p 39 || |p 40 || |p 41 || |p 42 || |p 43 || |p 44 || |p 45 || |p 46 || |p 47 || |p 48 || |p 49 || |p 50 || Total sime= 46 N 26 |p 3 || [ 26 3|U 1 6 6] [ 26 3| 1 1U 11] [ 26 3| 2 2U 9] [ 26 3|U 3 5 5] [ 26 3| 3 3U 7] [ 26 3| 4 4U 5] |p 4 || [ 26 4| 1 1 12 12] [ 26 4| 2 2 11 11] [ 26 4| 3 3 10 10] [ 26 4| 4 4 9 9] [ 26 4| 5 5 8 8] [ 26 4| 6 6 7 7] |p 5 || [ 26 5|U 1 7 7 12 12] [ 26 5|U 1 8 8 11 11] [ 26 5|U 1 9 9 10 10] [ 26 5| 2 2U 11 12 12] [ 26 5|U 3 6 6 12 12] [ 26 5|U 3 7 7 11 11] [ 26 5|U 3 8 8 10 10] [ 26 5|U 3 9 9 9 9] [ 26 5| 3 3U 9 12 12] [ 26 5| 3 3U 11 11 11] [ 26 5| 4 4U 7 12 12] [ 26 5| 4 4U 9 11 11] [ 26 5| 4 4 10 10U 11] [ 26 5|U 5 5 5 12 12] [ 26 5|U 5 6 6 11 11] [ 26 5|U 5 7 7 10 10] [ 26 5| 5 5U 7 11 11] [ 26 5|U 5 8 8 9 9] [ 26 5| 5 5U 9 10 10] [ 26 5| 5 5 9 9U 11] [ 26 5| 6 6U 7 10 10] [ 26 5| 6 6 8 8U 11] [ 26 5| 6 6U 9 9 9] [ 26 5|U 7 7 7 9 9] [ 26 5| 7 7 7 7U 11] [ 26 5|U 7 8 8 8 8] [ 26 5| 7 7 8 8U 9] |p 6 || [ 26 6| 2 2 12 12 12 12] [ 26 6| 3 3 11 11 12 12] [ 26 6| 4 4 10 10 12 12] [ 26 6| 4 4 11 11 11 11] [ 26 6| 5 5 9 9 12 12] [ 26 6| 5 5 10 10 11 11] [ 26 6| 6 6 8 8 12 12] [ 26 6| 6 6 9 9 11 11] [ 26 6| 6 6 10 10 10 10] [ 26 6| 7 7 7 7 12 12] [ 26 6| 7 7 8 8 11 11] [ 26 6| 7 7 9 9 10 10] [ 26 6| 8 8 8 8 10 10] [ 26 6| 8 8 9 9 9 9] |p 7 || [ 26 7|U 1 8 8 12 12 12 12] [ 26 7|U 1 9 9 11 11 12 12] [ 26 7|U 1 10 10 10 10 12 12] [ 26 7|U 1 10 10 11 11 11 11] [ 26 7|U 3 7 7 12 12 12 12] [ 26 7|U 3 8 8 11 11 12 12] [ 26 7|U 3 9 9 10 10 12 12] [ 26 7|U 3 9 9 11 11 11 11] [ 26 7|U 3 10 10 10 10 11 11] [ 26 7| 3 3U 11 12 12 12 12] [ 26 7| 4 4U 9 12 12 12 12] [ 26 7| 4 4U 11 11 11 12 12] [ 26 7|U 5 6 6 12 12 12 12] [ 26 7|U 5 7 7 11 11 12 12] [ 26 7| 5 5U 7 12 12 12 12] [ 26 7|U 5 8 8 10 10 12 12] [ 26 7|U 5 8 8 11 11 11 11] [ 26 7|U 5 9 9 9 9 12 12] [ 26 7|U 5 9 9 10 10 11 11] [ 26 7| 5 5U 9 11 11 12 12] [ 26 7|U 5 10 10 10 10 10 10] [ 26 7| 5 5 10 10U 11 12 12] [ 26 7| 5 5U 11 11 11 11 11] [ 26 7| 6 6U 7 11 11 12 12] [ 26 7| 6 6U 9 10 10 12 12] [ 26 7| 6 6U 9 11 11 11 11] [ 26 7| 6 6 9 9U 11 12 12] [ 26 7| 6 6 10 10U 11 11 11] [ 26 7|U 7 7 7 10 10 12 12] [ 26 7|U 7 7 7 11 11 11 11] [ 26 7|U 7 8 8 9 9 12 12] [ 26 7|U 7 8 8 10 10 11 11] [ 26 7| 7 7 8 8U 11 12 12] [ 26 7|U 7 9 9 9 9 11 11] [ 26 7| 7 7U 9 9 9 12 12] [ 26 7|U 7 9 9 10 10 10 10] [ 26 7| 7 7U 9 10 10 11 11] [ 26 7| 7 7 9 9U 11 11 11] [ 26 7| 7 7 10 10 10 10U 11] [ 26 7| 8 8 8 8U 9 12 12] [ 26 7| 8 8 8 8U 11 11 11] [ 26 7| 8 8U 9 9 9 11 11] [ 26 7| 8 8U 9 10 10 10 10] [ 26 7| 8 8 9 9 10 10U 11] [ 26 7|U 9 9 9 9 9 10 10] [ 26 7| 9 9 9 9 9 9U 11] |p 8 || [ 26 8| 3 3 12 12 12 12 12 12] [ 26 8| 4 4 11 11 12 12 12 12] [ 26 8| 5 5 10 10 12 12 12 12] [ 26 8| 5 5 11 11 11 11 12 12] [ 26 8| 6 6 9 9 12 12 12 12] [ 26 8| 6 6 10 10 11 11 12 12] [ 26 8| 6 6 11 11 11 11 11 11] [ 26 8| 7 7 8 8 12 12 12 12] [ 26 8| 7 7 9 9 11 11 12 12] [ 26 8| 7 7 10 10 10 10 12 12] [ 26 8| 7 7 10 10 11 11 11 11] [ 26 8| 8 8 8 8 11 11 12 12] [ 26 8| 8 8 9 9 10 10 12 12] [ 26 8| 8 8 9 9 11 11 11 11] [ 26 8| 8 8 10 10 10 10 11 11] [ 26 8| 9 9 9 9 9 9 12 12] [ 26 8| 9 9 9 9 10 10 11 11] [ 26 8| 9 9 10 10 10 10 10 10] |p 9 || [ 26 9|U 1 9 9 12 12 12 12 12 12] [ 26 9|U 1 10 10 11 11 12 12 12 12] [ 26 9|U 1 11 11 11 11 11 11 12 12] [ 26 9|U 3 8 8 12 12 12 12 12 12] [ 26 9|U 3 9 9 11 11 12 12 12 12] [ 26 9|U 3 10 10 10 10 12 12 12 12] [ 26 9|U 3 10 10 11 11 11 11 12 12] [ 26 9|U 3 11 11 11 11 11 11 11 11] [ 26 9| 4 4U 11 12 12 12 12 12 12] [ 26 9|U 5 7 7 12 12 12 12 12 12] [ 26 9|U 5 8 8 11 11 12 12 12 12] [ 26 9|U 5 9 9 10 10 12 12 12 12] [ 26 9|U 5 9 9 11 11 11 11 12 12] [ 26 9| 5 5U 9 12 12 12 12 12 12] [ 26 9|U 5 10 10 10 10 11 11 12 12] [ 26 9|U 5 10 10 11 11 11 11 11 11] [ 26 9| 5 5U 11 11 11 12 12 12 12] [ 26 9| 6 6U 7 12 12 12 12 12 12] [ 26 9| 6 6U 9 11 11 12 12 12 12] [ 26 9| 6 6 10 10U 11 12 12 12 12] [ 26 9| 6 6U 11 11 11 11 11 12 12] [ 26 9|U 7 7 7 11 11 12 12 12 12] [ 26 9|U 7 8 8 10 10 12 12 12 12] [ 26 9|U 7 8 8 11 11 11 11 12 12] [ 26 9|U 7 9 9 9 9 12 12 12 12] [ 26 9|U 7 9 9 10 10 11 11 12 12] [ 26 9| 7 7U 9 10 10 12 12 12 12] [ 26 9|U 7 9 9 11 11 11 11 11 11] [ 26 9| 7 7U 9 11 11 11 11 12 12] [ 26 9| 7 7 9 9U 11 12 12 12 12] [ 26 9|U 7 10 10 10 10 10 10 12 12] [ 26 9|U 7 10 10 10 10 11 11 11 11] [ 26 9| 7 7 10 10U 11 11 11 12 12] [ 26 9| 7 7U 11 11 11 11 11 11 11] [ 26 9| 8 8 8 8U 11 12 12 12 12] [ 26 9| 8 8U 9 9 9 12 12 12 12] [ 26 9| 8 8U 9 10 10 11 11 12 12] [ 26 9| 8 8U 9 11 11 11 11 11 11] [ 26 9| 8 8 9 9U 11 11 11 12 12] [ 26 9| 8 8 10 10 10 10U 11 12 12] [ 26 9| 8 8 10 10U 11 11 11 11 11] [ 26 9|U 9 9 9 9 9 11 11 12 12] [ 26 9|U 9 9 9 10 10 10 10 12 12] [ 26 9|U 9 9 9 10 10 11 11 11 11] [ 26 9| 9 9 9 9 10 10U 11 12 12] [ 26 9| 9 9 9 9U 11 11 11 11 11] [ 26 9|U 9 10 10 10 10 10 10 11 11] [ 26 9| 9 9 10 10 10 10U 11 11 11] [ 26 9| 10 10 10 10 10 10 10 10U 11] |p 10 || [ 26 10| 4 4 12 12 12 12 12 12 12 12] [ 26 10| 5 5 11 11 12 12 12 12 12 12] [ 26 10| 6 6 10 10 12 12 12 12 12 12] [ 26 10| 6 6 11 11 11 11 12 12 12 12] [ 26 10| 7 7 9 9 12 12 12 12 12 12] [ 26 10| 7 7 10 10 11 11 12 12 12 12] [ 26 10| 7 7 11 11 11 11 11 11 12 12] [ 26 10| 8 8 8 8 12 12 12 12 12 12] [ 26 10| 8 8 9 9 11 11 12 12 12 12] [ 26 10| 8 8 10 10 10 10 12 12 12 12] [ 26 10| 8 8 10 10 11 11 11 11 12 12] [ 26 10| 8 8 11 11 11 11 11 11 11 11] [ 26 10| 9 9 9 9 10 10 12 12 12 12] [ 26 10| 9 9 9 9 11 11 11 11 12 12] [ 26 10| 9 9 10 10 10 10 11 11 12 12] [ 26 10| 9 9 10 10 11 11 11 11 11 11] [ 26 10| 10 10 10 10 10 10 10 10 12 12] [ 26 10| 10 10 10 10 10 10 11 11 11 11] |p 11 || [ 26 11|U 1 10 10 12 12 12 12 12 12 12 12] [ 26 11|U 1 11 11 11 11 12 12 12 12 12 12] [ 26 11|U 3 9 9 12 12 12 12 12 12 12 12] [ 26 11|U 3 10 10 11 11 12 12 12 12 12 12] [ 26 11|U 3 11 11 11 11 11 11 12 12 12 12] [ 26 11|U 5 8 8 12 12 12 12 12 12 12 12] [ 26 11|U 5 9 9 11 11 12 12 12 12 12 12] [ 26 11|U 5 10 10 10 10 12 12 12 12 12 12] [ 26 11|U 5 10 10 11 11 11 11 12 12 12 12] [ 26 11|U 5 11 11 11 11 11 11 11 11 12 12] [ 26 11| 5 5U 11 12 12 12 12 12 12 12 12] [ 26 11| 6 6U 9 12 12 12 12 12 12 12 12] [ 26 11| 6 6U 11 11 11 12 12 12 12 12 12] [ 26 11|U 7 7 7 12 12 12 12 12 12 12 12] [ 26 11|U 7 8 8 11 11 12 12 12 12 12 12] [ 26 11|U 7 9 9 10 10 12 12 12 12 12 12] [ 26 11|U 7 9 9 11 11 11 11 12 12 12 12] [ 26 11| 7 7U 9 11 11 12 12 12 12 12 12] [ 26 11|U 7 10 10 10 10 11 11 12 12 12 12] [ 26 11|U 7 10 10 11 11 11 11 11 11 12 12] [ 26 11| 7 7 10 10U 11 12 12 12 12 12 12] [ 26 11|U 7 11 11 11 11 11 11 11 11 11 11] [ 26 11| 7 7U 11 11 11 11 11 12 12 12 12] [ 26 11| 8 8U 9 10 10 12 12 12 12 12 12] [ 26 11| 8 8U 9 11 11 11 11 12 12 12 12] [ 26 11| 8 8 9 9U 11 12 12 12 12 12 12] [ 26 11| 8 8 10 10U 11 11 11 12 12 12 12] [ 26 11| 8 8U 11 11 11 11 11 11 11 12 12] [ 26 11|U 9 9 9 9 9 12 12 12 12 12 12] [ 26 11|U 9 9 9 10 10 11 11 12 12 12 12] [ 26 11|U 9 9 9 11 11 11 11 11 11 12 12] [ 26 11| 9 9 9 9U 11 11 11 12 12 12 12] [ 26 11|U 9 10 10 10 10 10 10 12 12 12 12] [ 26 11|U 9 10 10 10 10 11 11 11 11 12 12] [ 26 11| 9 9 10 10 10 10U 11 12 12 12 12] [ 26 11|U 9 10 10 11 11 11 11 11 11 11 11] [ 26 11| 9 9 10 10U 11 11 11 11 11 12 12] [ 26 11| 9 9U 11 11 11 11 11 11 11 11 11] [ 26 11| 10 10 10 10 10 10U 11 11 11 12 12] [ 26 11| 10 10 10 10U 11 11 11 11 11 11 11] |p 12 || [ 26 12| 5 5 12 12 12 12 12 12 12 12 12 12] [ 26 12| 6 6 11 11 12 12 12 12 12 12 12 12] [ 26 12| 7 7 10 10 12 12 12 12 12 12 12 12] [ 26 12| 7 7 11 11 11 11 12 12 12 12 12 12] [ 26 12| 8 8 9 9 12 12 12 12 12 12 12 12] [ 26 12| 8 8 10 10 11 11 12 12 12 12 12 12] [ 26 12| 8 8 11 11 11 11 11 11 12 12 12 12] [ 26 12| 9 9 9 9 11 11 12 12 12 12 12 12] [ 26 12| 9 9 10 10 10 10 12 12 12 12 12 12] [ 26 12| 9 9 10 10 11 11 11 11 12 12 12 12] [ 26 12| 9 9 11 11 11 11 11 11 11 11 12 12] [ 26 12| 10 10 10 10 10 10 11 11 12 12 12 12] [ 26 12| 10 10 10 10 11 11 11 11 11 11 12 12] [ 26 12| 10 10 11 11 11 11 11 11 11 11 11 11] |p 13 || |p 14 || |p 15 || |p 16 || |p 17 || |p 18 || |p 19 || |p 20 || |p 21 || |p 22 || |p 23 || |p 24 || |p 25 || |p 26 || |p 27 || |p 28 || |p 29 || |p 30 || |p 31 || |p 32 || |p 33 || |p 34 || |p 35 || |p 36 || |p 37 || |p 38 || |p 39 || |p 40 || |p 41 || |p 42 || |p 43 || |p 44 || |p 45 || |p 46 || |p 47 || |p 48 || |p 49 || |p 50 || |p 51 || |p 52 || Total sime= 238

Véanse también los polígonos también simétricos:

Polígonos estrellados en red N

Polígonos central simétricos en red N

Poligonos regulares en red N

Poligonos cualesquiera en red N

---

Vuelta al Principio     Última actualización:   Sunday, 21 de April de 2013   Visitantes: