Esta página está en construcción: perdonen los errores, repeticiones y temas inacabados.
This page is being developed: I am sorry for errors, duplications and unfinished subjects.
Polígonos regulares en red N (perteneciente a Decoración Geométrica Islámica)
La red divide el plano en muchos polígonos elementales cuya reunión lo cubre. La conocida fórmula
Caras + Vértices = Aristas +2 (2’)
se cumple también en el plano, ya que podemos considerarlo como una figura en el espacio proyectada sobre ese plano, con una cara trasera que cierra la figura espacial (pensemos en un sobre de carta como un tetraedro visto desde arriba). En este caso, caras son polígonos, aristas son lados y vértices, vértices.
Cualquier polígono cerrado en esta red tendrá un múltiplo de a en cada vértice. Si tiene p vértices (polígono-p), la suma de sus ángulos interiores vale, usando (1): p (p-2)= a N/2(p-2)= a N (p/2 - 1); y el ángulo interior medio, igual a cada uno de los del polígono-p regular: aim = a N (p-2)/2p:
aim = a N (1/2 – 1/ p) o, en índices iim = N (1/2 – 1/ p) (2”)
valor que no siempre es entero, lo que quiere decir que no en todas las redes hay polígonos-p regulares; esto ocurre sólo si N es múltiplo del paréntesis. Haciendo N = k p:
iim = N (1/2 – 1/ p) = k p (1/2 – 1/ p) = k p/ 2 – k = k/2 ( p –2)
con lo que iim (número de a de la red en cada vértice interior) es entero si 1º. k es entero par, o 2º. si lo es (p-2), es decir, p, que es siempre entero pero impar a veces. Incluso pudiera admitirse k no entero (p no divisor de N) si es par k (p-2). Hemos determinado pues hasta ahora la posibilidad de existencia de un polígono-p regular con sus lados sobre la red N [1].
Consideremos ahora el número q de polígonos regulares p que pueden coincidir en un vértice de una cubrición del plano mediante esos polígonos. Si q es entero su unión cubre en efecto el plano; si no, no lo cubre, se solapan o faltan los polígonos alrededor del vértice, y no hay cubrición adecuada.
Una manera eficaz de describir y codificar cómo se organizan estas baldosas cubrientes del plano, debida a Schläfli, es el código {p,q}, que nos dice que en todo vértice de una cubrición del plano compuesta por polígonos regulares de p vértices coinciden q polígonos; o sea, suman 360º o 2p radianes [ q ( p (p-2) / p) = 2p ] lo que conduce a
(p-2) (q-2) = 4 p, q > 2 (2”’)
Sabiendo que tanto p como q son enteros, probaremos hasta encontrar todas las cubriciones posibles, o sea las soluciones de la ecuación anterior, que son
|
Recubrimiento |
p |
q |
{p,q} |
|
Triángulos |
3 |
6 |
{3,6} |
|
Cuadrados |
4 |
4 |
{4,4} |
|
Hexágonos |
6 |
3 |
{6,3} |
es decir, muy pocas. Como veremos en P9, son los dos últimos casos, ligados a N=8 y N=12, los cómodos y preferidos para recubrir el plano.
Uniendo ahora ambas ideas, polígonos-p regulares y cubrición del plano con ellos, todo ello en red N, listamos ahora los valores N, k, i, q, imponiendo que i sea entero positivo y menor que N/2 (es decir que el polígono sea convexo (no estrellado), con todos sus ángulos interiores menores que dos rectos (180º). Asimismo q>2 (más de dos polígonos-p en el vértice) y, si cubre, entero (q=3, 4, 5..)..
| POLÍGONOS REGULARES EN RED N. en red N, pueden trazarse polígonos regulares de p ángulos (iguales) cada uno con i ángulos alfa de red N, y coincidiendo q polígonos en cada vértice i = N . (1 / 2 - 1 / p) i<N/2 , entero N = k.p = i.q _________________________________________________ N [p1 k1 i1 q1] [p2 k2 i2 q2] ... _________________________________________________ 3 ||[ 6 .5 1 3] 4 [ 4 1 1 4] 5 ||[ 10 .5 2 2.5] 6 [ 3 2 1 6][ 6 1 2 3] 7 ||[ 14 .5 3 2.33] 8 [ 4 2 2 4][ 8 1 3 2.67] 9 [ 6 1.5 3 3] ||[ 18 .5 4 2.25] 10 [ 5 2 3 3.33][ 10 1 4 2.5] 11 ||[ 22 .5 5 2.2] 12 [ 3 4 2 6][ 4 3 3 4][ 6 2 4 3][ 12 1 5 2.4] 13 ||[ 26 .5 6 2.17] 14 [ 7 2 5 2.8][ 14 1 6 2.33] 15 [ 6 2.5 5 3][ 10 1.5 6 2.5] ||[ 30 .5 7 2.14] 16 [ 4 4 4 4][ 8 2 6 2.67][ 16 1 7 2.29] 17 ||[ 34 .5 8 2.13] 18 [ 3 6 3 6][ 6 3 6 3][ 9 2 7 2.57][ 18 1 8 2.25] 19 ||[ 38 .5 9 2.11] 20 [ 4 5 5 4][ 5 4 6 3.33][ 10 2 8 2.5][ 20 1 9 2.22] 21 [ 6 3.5 7 3][ 14 1.5 9 2.33] ||[ 42 .5 10 2.1] 22 [ 11 2 9 2.44][ 22 1 10 2.2] 23 ||[ 46 .5 11 2.09] 24 [ 3 8 4 6][ 4 6 6 4][ 6 4 8 3][ 8 3 9 2.67][ 12 2 10 2.4][ 24 1 11 2.18] 25 [ 10 2.5 10 2.5] ||[ 50 .5 12 2.08] 26 [ 13 2 11 2.36][ 26 1 12 2.17] 27 [ 6 4.5 9 3][ 18 1.5 12 2.25] ||[ 54 .5 13 2.08] 28 [ 4 7 7 4][ 7 4 10 2.8][ 14 2 12 2.33][ 28 1 13 2.15] 29 ||[ 58 .5 14 2.07] 30 [ 3 10 5 6][ 5 6 9 3.33][ 6 5 10 3][ 10 3 12 2.5][ 15 2 13 2.31][ 30 1 14 2.14] 31 ||[ 62 .5 15 2.07] 32 [ 4 8 8 4][ 8 4 12 2.67][ 16 2 14 2.29][ 32 1 15 2.13] 33 [ 6 5.5 11 3][ 22 1.5 15 2.2] ||[ 66 .5 16 2.06] 34 [ 17 2 15 2.27][ 34 1 16 2.13] 35 [ 10 3.5 14 2.5][ 14 2.5 15 2.33] ||[ 70 .5 17 2.06] 36 [ 3 12 6 6][ 4 9 9 4][ 6 6 12 3][ 9 4 14 2.57][ 12 3 15 2.4][ 18 2 16 2.25][ 36 1 17 2.12] 37 ||[ 74 .5 18 2.06] 38 [ 19 2 17 2.24][ 38 1 18 2.11] 39 [ 6 6.5 13 3][ 26 1.5 18 2.17] ||[ 78 .5 19 2.05] 40 [ 4 10 10 4][ 5 8 12 3.33][ 8 5 15 2.67][ 10 4 16 2.5][ 20 2 18 2.22][ 40 1 19 2.11] |
| Cuadro 1. Poligonos Regulares En Red N. |
En el cuadro se observa que
0. Los valores muy divisibles de N admiten muchos polígonos regulares diferentes, ligados a sus divisores:
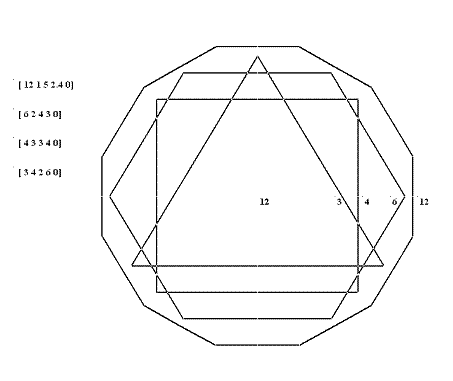
12 [ 3 2 4 ][ 4 3 3 ][ 6 4 2 ][ 12 5 1 ].
1. Solo los impares admiten k no entero (de la forma k = s / 2; s entero). Los ángulos interiores miden un número entero de mitades de a (ángulos de red), para un p necesariamente par, por ejemplo:
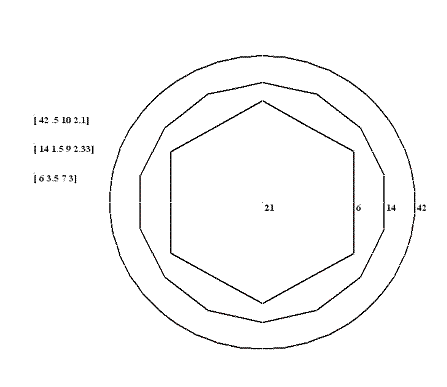
25 [ 10 10 2.5 ] ||[ 50 12 0.5 ]
2. Los primos sólo admiten un p=2N (k=1/2)
37 [ 74 18 0.5 ]
3. Si i no divide a n, q es fraccionario.
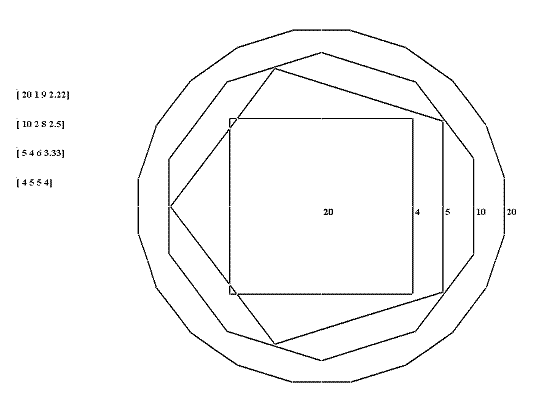
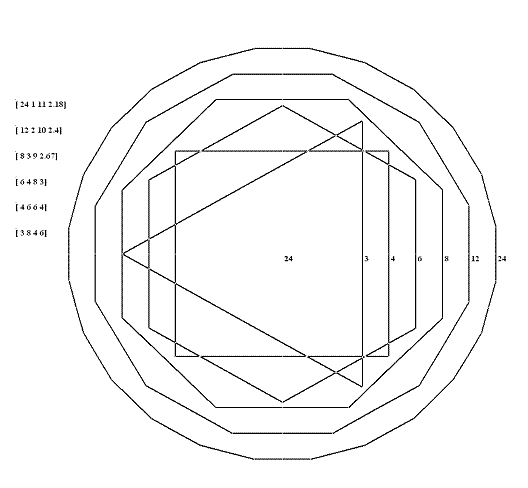
Veamos algunos ejemplos gráficos:
|
|
|
|
|
|
|
Fig. 0a, 0b |
|
|
|
|
|
|
|
|
Fig. 0c, 0d |
|
Hay que observar que estos polígonos regulares requieren igualdad de ángulos, sí, pero también de lados, lo que supone distancias iguales de esos lados al centro; esto sólo se cumplirá en general si ese centro es centro de un haz N.
En relación con estos polígonos regulares, véanse también:
Polígonos estrellados en red N Polígonos simétricos en red N Polígonos central simétricos en red N
[1] Hecho no siempre posible. Por ejemplo, en R10 no hay triángulos equiláteros en la red: sólo hay isósceles, de 36º-72º-72º.