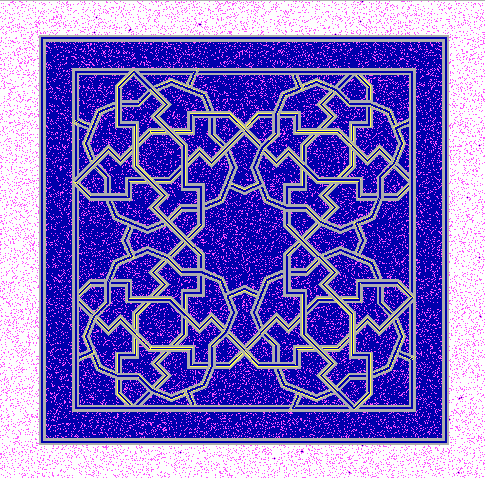
Lacería Islámica en paneles II (perteneciente a Decoración Geométrica Islámica)
PANEL 1. Introducción
Lacería Islámica en Paneles
La Lacería Islámica ‒arte, artesanía, decoración‒, constituye una bella y muy interesante aplicación del espíritu islámico. Islámico, aunque también ligado a las otras religiones del libro, judaísmo y cristianismo. Pero es sobre todo en el inmenso territorio que es o fue musulmán donde floreció esta particular expresión de la 'geometría expresiva'. Ante la prohibición coránica de la imaginería (religiosa y civil), lo árabes, turcos, persas e indios musulmanes aplicaron y aplican todavía ‒aunque con menos fervor‒, la lacería para revestir, adornar, mostrar y decir, llenando una función que la figura figurativa ha llenado en otras culturas y religiones.
Construida de madera, en techos, celosías, minbar (púlpito), puestas y ventanas, de estuco, en paredes, arcos, techos, de cerámica en suelos y paredes; en metal, marfil, cuero; labrado, moldeado, pintado, inciso, la lacería aparece por doquier en mil formas y diseños, sobre todo entre los siglos VIII a XVII, los siglos de esplendor del Islam.
Presentamos aquí, en paneles, una introducción teórica a este arte que permita una contemplación más rica y con más contenido ‒una comprensión‒, y una selección de algunas figuras elegidas por su interés didáctico, por su variedad o por su belleza.
Las figuras que aparecen en esta exposición han sido codificadas y realizadas mediante el programa de diseño por ordenador PUERTRA, escrito y aplicado por el autor de estos escrito, programa que contiene el modelo teórico descrito más adelante.
A lo largo de estos paneles, llamaremos a estas figuras Rige, acróstico de 'Redes Islámicas Geométricas Entrelazadas'. Sólo trataremos de figuras rectilíneas.
PARA SABER MÁSARDALAN, N. & BAKHTIAR, L. (1973) The Sense of Unity. Chicago: Chicago Press.
BOURGOIN, J. (1973) Arabic Geometrical Pattern & Design. N.York: Dover.
BURCKHARDT, T. (1976) Art of Islam. Language and Meaning. London: World of Islam Festival.
CABANELAS, D. (1988) "El Techo del Salón de Comares en la Alhambra". Granada: Patronato Alhambra.
CRITCHLOW, K. (1992) Islamic Patterns. London: Thames & Hudson.
NUERE, E. (1989) La Carpintería de Armar Española. Madrid: Ministerio Cultura.
NASR, S.H. (1987) Islamic Art and Spirituality. Ipswich, UK: Golgonooza.
PAVÓN MALDONADO, B. (1990) El Arte Hispano-Mulsulmán en su Decoración Geométrica. Madrid: Min. Cultura y Agencia Española de Cooperación Internacional.
PRIETO y VIVES, A. (1977) El Arte de la Lacería. Madrid: Colegio Ingen. Caminos, Canales y Puertos.
SÁNCHEZ, F.J. (1993-b.) "PUERTRA: a Model of Islamic Rectilinear Interlaced Lattices". Proc. ICEMCO. Cambridge: Univ. Cambridge.
SÁNCHEZ, F.J. (1995) "A Model of Islamic Rectilinear Interlaced Lattices".Dirección Internet: http:www.anglia.ac.uk/~trochford/puertra4.html
SÁNCHEZ, F.J. (1996) http://www.aldebaransoft.es/Laceria%20Islamica_Rige/decoracion_geometrica_islamica.htm
WILSON, J. (1983). Mosaic and Tessellated Patterns. N.York: Dover.
PANEL 2. Leyes Formales de la Rige.
Se observan las siguientes regularidades en estas figuras, constituyendo reglas que limitan sus posibilidades, lo cual crea así un estilo precisamente lo que llamamos aquí Rige.
R0. SUPERFICIE. Una Rige se desarrolla en una superficie. Sin embargo usan relieves para llenar huecos, y se sugiere el espacio mediante el recubrimiento (R11).
R1. RECTILÍNEAS. Sólo aparecen figuras limitadas por rectas ‒polígonos‒, aunque se usan curvas (palmas, frutos...) para llenar figuras, dulcificando así la sequedad y rigidez de la recta.
R2. DIRECCIONES. Todas esas rectas son paralelas a unas pocas direcciones en el plano, las que resultan al dividir la circunferencia (360º) en un número par N de sectores iguales. Este N es llamado el orden, y las N direcciones, las direcciones principales. Una de ellas es tomada como referencia, y llamada dirección 0, numerándose las demás sucesivamente según se gira en el sentido de las agujas del reloj (sentido tomado como +);
R3. DISTANCIAS. Todos los segmentos están situados sobre rectas determinadas, paralelas a las direcciones principales. Las distancias entre ellas son siempre iguales a unas pocas cantidades, 1, 2 o 3, y dependen del orden.
R4. RED. El conjunto de las N familias de paralelas el llamado la Red de la Rige, brevemente la N-red de esa Rige. Todos los segmentos están en la red, todas las figuras están en la red. Una Rige puede considerarse como una selección de las posibilidades que ofrece esa N-red.
R5. POLÍGONOS ELEMENTALES. Los segmentos forman polígonos, convexos o no. Aquellos que tienen otros segmentos de la red que les dividen son compuestos; los que no tienen segmentos dentro son simples, y serán llamadas Figuras Elementales o Elementos. Estos elementos son (casi) siempre simétricos respecto a un eje al menos.
R6. TAMAÑOS. Los tamaños de los elementos son similares: puede observarse un aspecto de densidad regular, recordando un tejido. Algunos elementos, que ayudan a cubrir la superficie son, no obstante, más pequeños (auxiliares).
R7. SIMETRÍA. Al menos un punto de simetría central puede encontrarse para toda la Rige; el orden (número de ejes) de esa simetría es o el orden de la Rige o el doble.
R8. TIRA. Los segmentos que forman los polígonos están unidos por sus extremos formando sobre la red tiras o cintas: líneas poligonales o caminos que nunca se interrumpen ‒salvo al cortar el dibujo: o bien se cierran dentro de él o son cortadas por sus límites, sugiriendo una longitud indefinida (las figuras reales son siempre limitadas, mientras que las redes son en esencia, infinitas).
R9. ANCHURA TIRA. La anchura de la tira o cinta es constante en una Rige. Cuando el grosor de la tira es máxima, cubre todo el plano, sin figuras intermedias, formando teselaciones. Alternativamente ese grosor puede ser nulo, reduciéndose la tira a una línea, y cubriendo el plano las figuras elementales, como mosaicos.
R10. CORTES. Cuando las tiras se cortan, lo hacen siempre sólo dos; su ángulo ‒nunca nulo‒ es siempre un múltiplo del ángulo básico, entre una y N-1 veces. Las tiran no se tuercen en la intersección, se cortan en partes rectas, con lo que ángulos opuestos en el cruce son iguales.
R11. RECUBRIMIENTO. La intersección suele representarse como un recubrimiento en el espacio. Cuando una tira cubre a otra en un cruce, es cubierta a su vez en sus dos cruces contiguos.
R12. CONSTRUCCIÓN. La forma o Rige puede ser considerada ‒y construida de hecho‒ como un conjunto de tiras que se cortan, apareciendo entonces las figuras elementales como los espacios entre esas tiras.
PANEL 3. Redes, Formas elementales y nombres.
RED de 6. Ángulos múltiples del básico, 360º/6=60º: 60º, 120º, 180º o llano; y sus correspondientes cóncavos (180º+60º, etc.).
Distancias múltiplos de un sólo valor: 1, 2, 3,...
Figuras elementales: estrella, celda de panal (exágono), diamante (rombo), puntas de flecha y lanza, bonetes, diábolo y montes bajo y alto (triángulos).
Caso muy simple. Esta red no es muy popular, debido a su sencillez y a una cierta pasividad o estabilidad extrema inherente.
RED de 8. Ángulos múltiples del básico, 360º/8=45º: 45º, 90º, 135º, 180º o llano; y sus correspondientes cóncavos (180º+45º, etc.).
Distancias múltiplos de dos valores: 1 y raíz cuadrada de 2,Ö2, o combinación de ellos: 2,
2 Ö2, Ö2-1, 2-Ö2, etc.
Figuras
elementales: estrellas (de 4 y 8), cuadrados, diamantes de frente (rombo) y de
lado, puntas de flecha y lanza, bonetes, diábolo, mariposa, casa, flechas de
caminos, montes bajo y alto (triángulos).
Esta red es la más frecuente, más que todas las demás juntas,
probablemente; ello es debido a su sencillez que permite no obstante variedad;
horizontales, verticales y oblicuas permiten jugar con libertad. Ángulos
rectos. Equilibrada y simbólica.
RED de 10. Ángulos múltiples del básico, 360º/10=36º: 72º, 108º, 144º, 180º o llano; y sus cóncavos.
Distancias múltiplos de dos valores: 1 y
F = (1+Ö5)/2 = 1.618..., o combinación de ellos: 2, 2F, F-1=0.618...=1/F, etc. Estas combinaciones del número de oro, están llenas de interesantes propiedades geométricas, aritméticas y numerológicas.Figuras elementales: estrellas (de 5 y 10), tambores, diamantes (rombo), puntas de flecha y lanza, bonetes, diábolo, mariposa, casa, flechas de caminos, montes bajo y alto (triángulos), montes con meseta, chincheta, pájaro, derviche, alas, sombreros, peto...
Esta red es la segunda más frecuente; sobre todo en mezquitas, quizá por su valor simbólico. Permite asimismo variedad y libertad; es menos estable que la anterior, no hay ángulos rectos.
OTRAS REDES. Tienen que ver con las anteriores, son múltiplos o combinaciones de ellas: 12, 16, 20, 24, 36. Órdenes mayores resultan ya confusos, aunque se encuentran, sobre todo en Marruecos.
PANEL 4. Construcción, Simetrías, Colores.
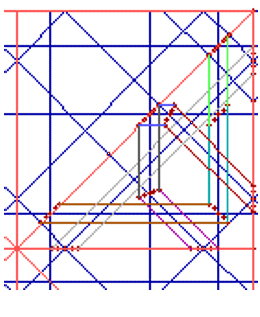La Rige presenta en
general múltiples parecidos entre sus partes: Simetrías de Eje, Simetrías
Centrales (rotaciones) y Traslaciones (desplazamientos) permiten generar toda
la forma en función de una de sus partes (cualidad que comparten con los
seres vivos). La más pequeña de esas partes (puede haber varias
posibilidades) es llamada Elemento Generador (EG).
Este EG suele tener forma de triángulo rectángulo, a veces de rectángulo. Uno de sus ángulos es igual al Ángulo Básico (ver Panel 2, R2).
La forma completa se genera habitualmente a partir del EG mediante cinco operaciones:
1. Una simetría del EG respecto a uno de los catetos del triangulo. Se genera así una forma simétrica.
2. Un giro de esa última forma alrededor de uno de los extremos del eje
anterior, donde se encuentra el ángulo básico. Se completa sí una forma con
simetría central, con N/2 lóbulos o formas semejantes, en círculo (N es el
Orden de la red, Panel 1, R2). Si en efecto el EG estaba dentro de un
triángulo rectángulo, y N es 8, se genera una cuadrado; asimismo si el EG
estaba dentro de un cuadrado. Si no, pueden producirse otras formas, según la
forma del EG y el valor de N. En todo caso la forma así generada se llama
Elem
ento de Traslación, por lo que ahora veremos.
3. Una repetición de esta última forma, ET, mediante
desplazamientos en direcciones horizontal y vertical lo que cubre el plano.
4. Los colores vienen a completar los efectos anteriores, añadiendo además su sensualidad y belleza. Generalmente acentúan las zonas de simetría circular, o las radiales (centro a periferia). Se destaca siempre la tira contra los elementos (Panel 2, R8 a R12), pues ambos constituyes dos espacios en oposición y dependencia mutua que deben ser adecuadamente destacados. Sin embargo, debe aplicarse cierta parquedad para evitar el colorín y la policromía banal ("dos colores son suficientes, tres son multitud", como se dice de los humanos).
5. Solo falta limitar esta forma indefinida mediante un recinto frontera, para obtener la Rige completa. Esta forma limitadora suele, bien formar parte de la red, bien acentuar las simetrías: el marco debe armonizar con la figura.
Todas estas operaciones, geométricas o no, crean nuevos efectos de conjunto y en las zonas de enlace de las partes simetrizadas o trasladadas. La forma adquiere así cualidades de sencillez, lo que la dota la hace perceptible, comprensible y pregnante (Gestalt ), desde el punto de vista psicológico. Estéticamente adquiere simplicidad (parsimonia), y unidad en su multiplicidad: resulta coherente y bella.
PANEL 5. Números, Simbología, Mística.
El Número es rey en este tipo de arte. Primero en toda la geometrización del espacio, que queda sometido a una rigurosa limitación, con unos pocos caminos posibles. También aparecen ligados al Orden de la red, en distancias entre rectas, en longitudes de segmentos, proporciones ilustres: Ö2 ligado a la red 8, Ö3, ligado al red 6, el número de oro, ligado a la red 10. Estos números ‒desesperación de los pitagóricos‒constituyen las redes y sus Riges.
Pero nos referimos sobre todo al número natural, el que sirve para contar, para multiplicar y dividir en el lenguaje corriente y en la intuición, como el Uno, el Dos, el Tres, el Cuatro, el Cinco, el Seis, el Siete. Estos primeros números ‒llamémoslos primordiales‒ tienen una gran importancia psicológica porque expresan, en sí mismos, nuestra concepción del mundo: cuando organizamos nuestro pensamiento, desde el habla natural al mito, elegimos siempre números que consolidan, por decirlo así, lo que queremos contar: aparecen así las Tres Hijas del Rey, los Siete Colores, los Cinco Sentidos, los Diez Mandamientos...
Números mayores sólo son aceptables como combinación de los anteriores: 10 es 2 por 5, 12 es 3 por 4, 4 por 3 y 6 por 2. Estas operaciones tienen una repercusión inmediata en lo visual, se perciben esos múltiplos y divisores como figuras de simetría de menor orden que la de la red. Un número primo alto, como el 41 no tiene aplicación en este ámbito: no 'dice' nada.
No es extraño que que esa perceptibilidad y expresividad inmediatas de estos números primordiales adquieran una significación que sobrepasa sus utilidades aritméticas, para devenir símbolos, dotados de connotaciones cercanos a lo místico. Los símbolos transcienden su carga semántica inicial y significan más, aunque quizá de manera más vaga y sugerente.
Asimismo, una vez devenidos símbolos, su aparición en cualquier contexto apunta a ellos, les cita: Decir 'tres' es apuntar o recordar también la Trinidad para un cristiano; decir 'noventa y nueve' es apuntar a los Nombres (conocidos) de Alá, para un musulmán.
Otro uso del número, muy ligado a las Tradiciones semitas (musulmana y judía), es el método o código Abjad. Atribuyendo cifras a cada letra del alfabeto, toda palabra adquiere también un número suma de los de sus letras. Así que toda palabra tiene un número asociado, y muchos números tienen una palabra ligada.
El artesano tradicional gusta de insertar mensajes, a menudo, cifrados, en su obra, que adquiere así para él más importancia y le impulsa a realizarla mejor, con más cariño. Al igual que el calígrafo musulmán elige para su artística escritura frases plenas de significado para él, el diseñador y constructor de una Rige, la prefiere llena que vacía: no se trata sólo de geometría, ni mucho menos.
El número de figuras que aparece en una Rige, por tanto, puede ser significativo, bien en el sentido primordial, bien en en el sentido de cita, bien en el sentido abjad. Y, desde luego, siempre influye enormemente en el aspecto, significado, lo que nos dice una forma como estas. Entender una Rige en sus múltiples mensajes y significados, constituye, pues, una larga (y apasíonante) tarea.
La figura completa, la Rige, aparece al observador como un mapa de significados esenciales, como un mandala, cuya contemplación, refleja, representa, explica ‒sin palabras‒ verdades fundamentales, es decir, Universales. El camino espiritual queda pues indicado.
PANEL 6. Arte, Belleza, Música.
Este Arte ‒pues alcanza este elevado grado‒ recuerda potentemente otro Arte sublime y abstracto: la Música, paradigma de la Harmonía y el Ritmo. La importancia del Número, la ausencia de discurso intelectual o representativo, su absorción mediante mecanismos no discursivos, son caracteres que ambos comparten. Veamos algunos constituyentes comunes.
El Ritmo es el primero y más obvio. Definiéndolo como el retorno regular de una forma o motivo ‒sonoro en música, visual en lacería‒ se encuentra en ésta última por doquier. En cualquier dirección elegida, recta o circular, se encuentra, con diferente período o distancia de repetición, una forma, igual porque ambas se pueden superponer, pero distinta porque ocurre en diferente lugar o momento (contexto). Esta regularidad de aparición produce un efecto de calma, de "quietud en el movimiento" según decía un místico sufí.
También la melodía encuentra su homóloga en la lacería. La divisiones del círculo tienen que ver con las escalas, como proporciones ‒angulares en la lacería, frecuenciales o tonales en la música‒ sencillas y por lo tanto perceptibles y agradables: he aquí la Consonancia redescubierta.
Incluso la Modulación y Enharmonía tiene aquí lugar: en efecto, se dan cambios de red en una superficie, incluso dentro de un mismo EG (elemento generador), como se ve en los últimos paneles ‒"Konya" por ejemplo.
El cambio de una división del círculo a otra, con algunas direcciones comunes, por continuidad perceptiva, equivale al cambio momentáneo de escala, modulación o metabolê, en una sección musical. La música islámica, en cuyos sistemas aparecen decenas, incluso cientos, de escalas presenta estas modulaciones con frecuencia, generalmente sobre un tetracordio: por ejemplo, Rast modula a Susnak, a Segah, a Nahauand y vuelve a Rast.
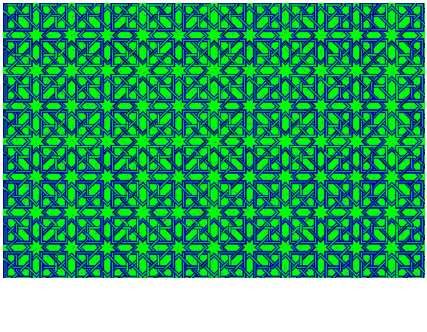Si
consideramos ahora la jerarquía relativa de las notas de una escala, también
la encontramos en las formas elementales de una Rige. Las más simétricas son
las más perceptibles, y por lo tanto las más importantes: son centros
de simetría y de percepción, tónicas visuales, el rey de
la escala. Las vecinas, menos simétricas, representan notas más disonantes,
hasta llegar a otros centros más simétricos ‒aunque menos que la tónica‒;
estos son las tónicas secundarias ‒quinta, dominante, repercussio,
el visir. Nuevos desplazamientos nos conducen a otro centro de
máxima simetría en otro punto: es la octava, tónica aguda o grave, el príncipe.
Así vemos otra vez que una Rige es una forma ilimitada: sólo el observador limita esas posibilidades, por incapacidades o por prisa. Cada uno, de acuerdo a su estado y desarrollo, percibe diferentes cosas en una forma. Y, cada vez que la contempla, aparecen cosas nuevas.
PANELES 7 - 16. Lista de Figuras.
Redes de 8, 16.
1. Alcázar 2. Azulejo.
3.Comares. 4.Alfo3
Redes de 10
5. Puertra. 6.Mevlut.
Redes de 12.
7. Alfo2. 8.Hexago.
Metabolai : Redes mixtas
9.Alfo1. Panel en ISFAHAN 10.Hani Caravanserai junto a Konya.
BREVES NOTAS sobre el AUTOR
Francisco Javier Sánchez González. Fundador y antiguo director del
Laboratorio de Tratamiento de Palabra y Música. Centro de Tecnologías Físicas. C.S.I.C. Serrano, 144. 28006-Madrid. Spain.
Tel. 918 491 228. Corr: javiersangonza@hotmail.com
Javier Sánchez (Doctor Ingeniero Industrial ‒Electrónica) ha creado y dirigido‒‒‒ el Laboratorio de Lingüística y Musicología, donde sus colaboradores y él mismo investigaron en Fonética, Métrica y Sintaxis dentro de la Lingüística y, en la Música, en Escalas Orientales, teoría de la Consonancia y desarrollo de herramientas de Análisis de la Señal. El Arte Islámico ‒lacería‒ fue también estudiado en el laboratorio.