Metabolai (perteneciente a Decoración Geométrica Islámica)

Introducción

Nos referimos con este término tomado de la música griega a una red de líneas que contiene mezclas de diferentes divisiones del círculo, en el contexto que hemos llamado Rige. Vea METABOLÊ para su introducción y definición.

Naturalmente, siempre es posible colocar un número cualquiera de redes vecinas y elegir sobre cada una de ellas una figura independiente, es decir, inconexa, de las demás. Esto significa, perceptivamente, tener varias Rige cercanas, pero no una Rige compleja. También podemos saltar de una a otra a través de las intersecciones de las familias de cada una de ellas con las demás. Se gana continuidad, pero aún quedan zonas independientes, queda una figura en trozos, por decirlo así. Se percibirán las zonas como separadas y el resultado no será placentero.

Se gana entonces verosimilitud cuando se colocan las redes de modo que tengan rectas comunes, mediante giros y traslaciones relativas de ellas. Los pasos de una a otra resultan más naturales. Por último se gana aún más verosimilitud, y belleza, cuando algunas (todas será probablemente imposible de las distancias básicas de ellas sean comunes para todas. En particular, la llamada calle suele ser común, resulta una verdadera calle de paso entre unas y otras, al modo de una calle ciudadana que une barrios diferentes de manera natural e incluso gradual. Uno se sorprende de pronto en ortro entorno estilístico y arquitectónico, representado en nuestro paradigma Rigeano por el orden y quebracidad , un parámetro geométrico-estético que mediremos y desarrollaremos en el lugar correspondiente (***)

La posibilidad teórica de una metabolê queda clara: dados dos de los tres vértices como pertenecientes a dos redes cualesquiera, siempre podemos encontrar otro quebrado cuyo valor complete el valor deseado, 1/2 con toda la precisión deseada, bastará elegir un denominador suficientemente alto. Por ejemplo si queremos cumplir la ecuación 1 con una aproximación de 1(10000), podemos elegir ese denominador, y ajustar el numerador en saltos de 1/10000 hasta que llegamos a la aproximación deseada..

Pero, naturalmente, estas soluciones no son satisfactorias desde el punto de vista artístico-perceptivo, porque esas redes son indistinguibles entre sí por el ojo. De modo que se buscan valores de n tan pequeños como sea posible; esto modifica el `problema que quedará así planteado:

Definición

Puesto que la suma de los ángulos interiores de un triángulo suman dos rectos, a + b + c = p  radianes, cuando estos ángulos pertenecen a redes enteras, es decir, son múltiplos de divisores enteros del ángulo que cubre todo el plano, m veces (2p/n), encontramos

m (2p/n)+ m' (2p/n') + m'' (2p/n'') = p                                                                  (0)

con lo que llegamos a la siguiente expresión , en dos formas equivalentes:

m /n + m'/n' + m''/n'' = 1/2                                                                                      (1)       

i=3

S ( m_i /n_i ) = 1/2                                                                                            (1')

i=1

en las que las tres fracciones son irreducibles (numerador y denominador son primps entre sí).

O sea, hay que hallar tres quebrados cuya suma es la mitad de la unidad (problema similar a partir medio queso tomando porciones pertenecientes a diferentes tipos de partición), y cuyos términos cumplen con las siguientes propiedades sencillas de las redes que concurren en el triángulo:

0 < m_i         2 < n_i             m_i < n_i < N         m_i, n_i  enteros positivos, primos entre si.          (3)

(numeradores pues no nulos, y denominadores, órdenes iguales a 3 o más.). N es un entero arbitrario, pequeño (en la práctica suele ser 36 como máximo, pero habitualmente vale entre 6 y 16), que adoptamos como límite de nuestra búsqueda; redes más complicadas (n alto) son siempre posibles pero el ojo es incapaz de percibir su diferencia con redes más sencillas aproximadamente divisoras o simplificadas de las otras (n = 16 es similar a n = 17, y por ello, también a n = 8).

Nótese que si en lugar del orden n de la correspondiente red, empleamos el semiorden, es decir, la mitad del número de divisiones del compás (cosa posible porque las redes interesantes son siempre pares ‒si no lo son, entonces sus rectas no coinciden al adosar los módulos de translación ET entre sí, como se ve laceria_islamica , por ejemplo), en lugar del término 1/2, encontraremos la unidad en nuestros cálculos.

Para polígonos con un número K de lados mayor que el triángulo (K=3), la expresión queda, teniendo en cuenta que cada ángulo suplementario añade dos rectos más a la suma de ángulos interiores):

i=K

S ( m_i / n_i ) = K/2 - 1                                                                                 (4)

i=1

Para el cuadrilátero valdría 1 la suma, pues (4/2-1).

Investiguemos ahora las posibilidades de metabolê que la fórmula (1) nos ofrece. Para ello demostremos primeramente el siguiente

Teorema:

                            Una metabolê de órdenes primos entre sí es imposible.

En efecto, pasando (1) a común denominador, se obtiene en general (suponiendo PES ‒primos entre sí‒ a los tres denominadores):

2mn'n''+2m'nn''+2m''nn'= nn'n''                                          (5)

y puesto que ambos términos son enteros e iguales, admiten los mismos divisores; en particular, n:

n (2mn'n''/n+2m'n''+2m''n') = n (n'n'')                                 (6)

y como también son enteros e iguales los paréntesis:

n' (2mn''/n + 2m'n''/n' + 2m'') = n'(n'')                                           (7)

Si el primer paréntesis es entero, y lo es por ser igual a n'', entero, lo son cada uno de sus sumandos, ya que todos son positivos (producto de positivos): luego n divide a 2mn'', y como no dividía a m por ser m/n irreducible, como vimos, deberá dividir a 2n'': entonces, o  n = 2, lo que quedó excluido en las condiciones (3) o divide a n" : así que no pueden ser PES n y n''.

asimismo n' ha de dividir a n'', al no poder hacerlo a m', (su numerador inicial) con lo que tampoco n' y n'' son PES. De modo que n divide a n' y por dividir n' a n'', también lo hace a n''.

 ¿Pero habrá en n' y n'' otros factores aparte de n?. No, porque si repetimos los razonamientos anteriores, de (3) a (5), para n', por un lado, y para n'', para otro, obtendremos asimismo que n' divide a los otros dos n, n''; y que n'' divide también a n y n'.

 Por lo tanto como todos son divisores de todos, todos son iguales, son el mismo:

n = n' = n''                                                                                 (8)

Esta contradicción de las hipótesis iniciales nos muestra que la metabolê verdadera de tres particiones PES, primas entre sí, es imposible:

El teorema queda demostrado.

Por lo tanto sólo una aproximación es quizá posible, una peudometabolê. Conservaremos para ella, si la hallamos, el nombre de metabolê, pero sabiendo que siempre se trata de aproximaciones, revalidadas o no por el ojo, sabia y artísticamente engañados por esos maestros de la fantasía que fueron (¿que son?) los pueblos del cercano oriente.

Pseudometabolê

Tenemos que considerar por tanto la pseodometabolê: así llamaremos a aquellas combinaciones que cumplen con la expresión principal solo de manera aproximada:

   m /n + m'/n' + m''/n'' = 1/2 + e                  (9) 

siendo e un término de error, pequeño frente a la unidad (por ejemplo, 1/20 en valor absoluto).

En la pseudometabolê del hane cerca de Konya 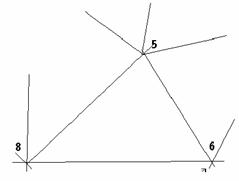(Turquía), en la figura adjunta, encontramos 1/8 +1/5 +1/6 = .9833 = 1- .0166 = 1/60, una apreciable aproximación según juzga el ojo, el cual sólo se percata del engaño, cuando ve que una de las rectas de la red presenta un cierta oscilación, serpentea ligeramente. En efecto el triángulo que une los centro de simetría de las particiones  de 12, arriba, 16, abajo y 10, a la derecha, la bisectriz del ángulo inferior (16) serpentea al prolongarla más allá del centro del triángulo. En ángulos el error es de 6 grados, bastante.

2.360/16  +  2.360/12 + 2.360/10 - 360 = 6 ^0,                             (10)

Para polígonos con un número K de lados mayor que el triángulo (K=3), la expresión queda, teniendo en cuenta que cada ángulo suplementario añade dos rectos más a la suma de ángulos interiores):

 anti=K

S ( m_i / n_i ) = K/2 - 1 +e                                      (11)

i=1

expresión general que recoge cualquier posibilidad de polígono cuyos ángulos pertenecen a redes distintas en general (pues varios de esos ángulos, incluso todos, pueden pertenecer a la misma). El rango del polígono (número de sus lados) está también limitado por el orden de las redes que en él intervienen, cuando consideramos polígonos convexos o estrellados`‒ de no ser así la introducción de ángulos cóncavos (mayores del llano) reabren por decirlo así la apertura de la reserva angular que se va agotando a al añadir ángulos convexos, lo cual permitiría un número ilimitado de lados en estos polígonos tan libres, como lo prueba la greca y figuras similares.

Naturalmente la fórmula (2) tiene infinitas soluciones; se diferenciarán y jerarquizarán entonces en función del grado de aproximación, pequeñez de e, con criterios extramatemáticos como sean la belleza y perceptibilidad del polígono resultante, cualidades que también están, por otra parte, ligados a esa pequeñez ‒más aproximación, más ilusión.

Metabolé en el dintel del caravanserei en Hani, cerca de Konya, Turquía.

Algunas metabolai

Hemos citado ya la metabolê konevi (nativa de Konya), cuyo esquema se ve en la figura anterior. Busquemos otros.

El primero que se nos aparece es sustituir el sumando 1/8, que no completaba el valor 1/2, por un valor parecido, 1/7, que lo cumple en exceso, pero incluso con más aproximación: en efecto, 1/8 +1/5 +1/7 = .5095 = 1- .0095 (casi 1/105), una excelente aproximación que tiene la ventaja de incluir una red poco frecuente, n7 o n14.

Pero realicemos una búsqueda sistemática probando todos los triángulos posibles dos al menos de sus ángulos pertenecientes a redes diferentes con 20 o menos lados, y con aproximación mejor que 1/100 = .01:

CALmetab(olê). METABOLAI. 06-30-1997. Err< 1E-002 ‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒ Conta semiórdenes coeficientes  error   en ángulos    Met 1:  n: 4 7 9  m: 1 1 1 err: 0.00397 ang: 0.114 º Met 2:  n: 4 7 10 m: 1 1 1 err:-0.00714 ang:-0.205 º Met 3:  n: 4 8 8  m: 1 1 1 err: 0.00000 ang: 0.000 º Met 4:  n: 5 5 10 m: 1 1 1 err: 0.00000 ang: 0.000 º Met 5:  n: 5 6 7  m: 1 1 1 err: 0.00952 ang: 0.273 º Met 6:  n: 5 6 8  m: 1 1 1 err:-0.00833 ang:-0.239 º Met 7:  n: 5 5 10 m: 1 1 1 err: 0.00000 ang: 0.000 º Met 8:  n: 6 9 9  m: 1 1 2 err: 0.00000 ang: 0.000 º Met 9:  n: 6 9 9  m: 1 2 1 err: 0.00000 ang: 0.000 º Met 10: n: 7 7 9  m: 1 1 2 err: 0.00794 ang: 0.227 º Met 11: n: 7 8 9  m: 1 1 2 err:-0.00992 ang:-0.284 º Met 12: n: 7 9 9  m: 2 1 1 err: 0.00794 ang: 0.227 º Met 13: n: 7 9 10 m: 2 1 1 err:-0.00317 ang:-0.091 º

(Pseudo)metabolai de órdenes bajos.

Obtenemos, según se ve en la figura, 13 metabolai con esas condiciones; pero se ve enseguida que la 4 y 7 son iguales, y reducibles a su vez a una sola red de 10; asimismo la 3 se reduce a red de 8, y la 8 y la 9 son iguales: así que quedan sólo 13 - 4 = 9 que son verdaderas metabolai (es decir, pseudometabolai). Nótese que la 5 y 6 son las ya citadas al principio de esta sección.

Distancias

Una vez obtenidos los ángulos del triángulo metabólico buscado, se trata de encontrar las distancias de cada red de la metabolê. Como decíamos al principio (***) haremos común una de las las distancias de cada una de las tres redes, la calle, cuyo valor consideramos la unidad de medida. La otra distancia, función de ella quedará fijada en cada una de las redes. Busquemos su valor aplicando la fórmula () modificada, la ().

Veamos ahora otros casos poco corrientes, de 6 a 13, que aportan pseudometabolai sorprendentes como 7-11-12, o 7-6-13, con los triángulos respectivos representados junto a los datos. Los cálculos y dibujos provienen de nuestro programa CalMetab..

Aparecen para cada solución un numeral interno del programa, los valores de los semi-órdenes (el número de direcciones diferentes que admite la red, la mitad del número máximo de radios que admite la red en un punto cualquiera) los coeficientes del ángulo unitario de cada orden en el triángulo solución, los ángulos así obtenidos, el error angular total en el triángulo (sobre dos rectos) y un factor de arbitrario calidad, definido como

Calidad = abs (1 / (m1 / n1 + m2 / n2 + m3 / n3-.5) / n3 )                                        (12)

que no es más que el error angular en el triángulo (exceso o defecto a dos rectos) invertido (más error, menos calidad) y ponderado además con el último de los tres denominadores, el mayor en nuestro cálculo; ponderamos porque ya vimos que el error puede hacerse ínfimo subiendo indefinidamente los órdenes de las redes, caso trivial no revalidado por el ojo.

Una calidad de 999 representa, como código arbitrario, no como verdadero valor, una calidad infinita, no error: es .9999999999, o sea, 1.

Puede verse otro estudio particular de una Metabolê en  ISFAHAN

Retomamos el tema en 2008: metabolai II.

 

---

Vuelta al Principio     Última actualización  miércoles, 05 de septiembre de 2018    Visitantes: