Distancia y ángulos en redes periódicas de 12 (perteneciente a Decoración Geométrica Islámica)
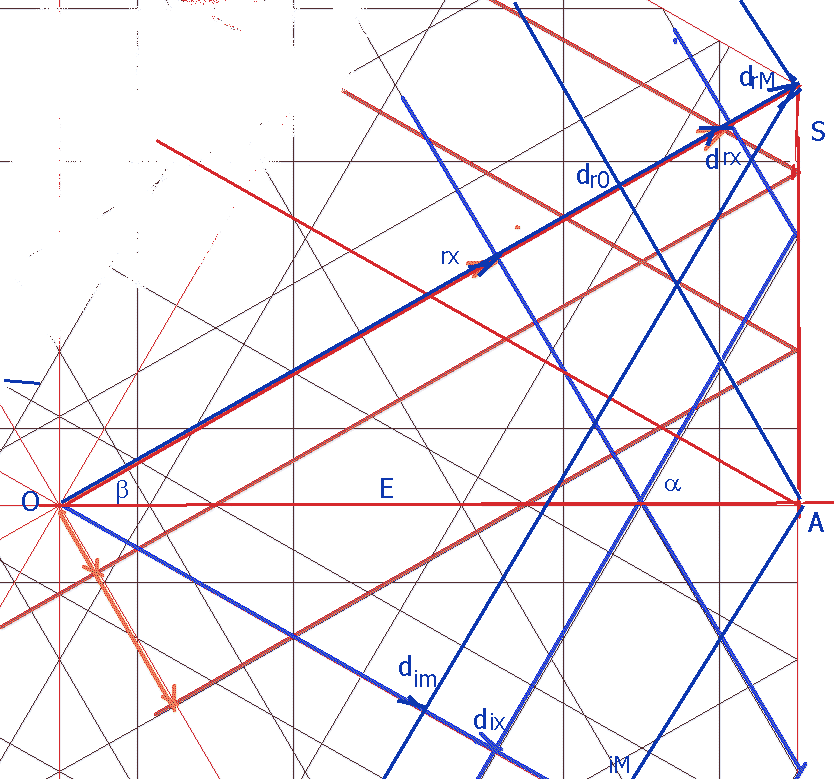
De modo que nos enteramos ahora de que:
1. La suma de las distancias de los rayos incidente y reflejado en constante. De modo que lo que en una serie determinada (determinada por su ángulo ai) se van separando los incidentes, va aumentando en los reflejados. Así se ve en los rayos rosa de la figura 1, uno a distancia c/2 , la primera, que se refleja en la cuarta, a distancia c/2+c+a+c. Si nos fijamos en el otro, de incidente a distancia c/2+c, la segunda, vemos que se refleja en la tercera distancia, c/2+c+a. De modo que lo que aumenta el incidente, en este caso la distancia a, lo disminuye la reflejada, en igual cantidad. Igual comportamiento presentan la serie de 60º, en azul, que alterna las distancias 2ª y 4ª con las 4ª y 3ª , con diferencia constante también en este caso.
O sea, para el par de rayos incidente y reflejado se cumple:
1. la suma de distancias d es constante: ej.: (c/2+c+a+c)+(c/2) = (c/2+c+a)+ (c/2+c) en serie 30º. Que es igual a la última distancia, en este caso la quinta, (c/2+c+a+c+c/2)
2. la diferencia de distancias es creciente con constantes. (c/2+c+a+c)-(c/2) = (c/2+c+a)-(c/2+c)
En relación a las semisecuencias X y H el par que nos definen todas las series de distancias, repitiéndose alternadamente en todos los ángulos, tenemos que cualquier elemento s de una semisecuencia define una distancia al origen igual a la suma de todas las anteriores con ella misma.:
di = S1-i si
dr = S1-i sr
di + dr = df
Es decir, si el rayo incidente abarca los primeros elementos de la semisecuencia, el reflejado abarca los restantes, que deben coincidir con loa primeros hasta un punto que equidista del centro.
Esto nos conduce al carácter capicúa de la semisecuencia que encontrábamos empíricamente en la página Redes periódicas de 12 y Diseño de redes de 8
dr = S1-i sr
dr = df - S1-i sr
Condiciones de reflejo en SS
| Condiciones de Periodicidad mediante rayos en reflejo | ||
| m0 mu an_in porc.cent.capicua | ||
| Red 8 | 0 0 0.00 9999.00 0 1 45.00 100.00 0 2 90.00 0.00 0 3 135.00 -100.00 ‒‒‒‒‒‒‒‒‒-
0.5 0 22.50 241.42 |
|
| Red 10 | 0 0 0.00 9999.00 0 1 36.00 100.00 0 2 72.00 23.61 0 3 108.00 -23.61 0 4 144.00 -100.00 ‒‒‒‒‒‒‒‒‒-
0.5 0 18.00 223.61 |
|
| Red 12 |
Red 12 __________________________________________________________________ m0 mu an_in %.cnt.cap n.dist SS Lm.Inf,Cent,Lm.Supe SS%- ....no semigiro inicial..... 0 0 0.0 101.00% 5 0 1 3 5 : [|çc/a\cç|]: [//çcacç] 0 2 60.0 33.33% 5 0 2 3 4 : [ç|c/a\c|ç]: [//çcacç] 0 4 120.0 33.33% 5 0 2 3 4 : [ç|c/a\c|ç]: [//çcacç] 0 1 30.0 100.00% 5 1 1 3 5 : [|ça/c\aç|]: [//çacaç] 0 3 90.0 0.00% 5 1 3 3 3 : [ça|/c\|aç]: [//çacaç] 0 5 150.0 100.00% 5 1 1 3 5 : [|ça/c\aç|]: [//çacaç] ....semigirado inicial..... 0.5 0 15.0 215.47% 5 0 1 3 5 : [|çc/a\cç|]: [//çcacç] 0.5 2 75.0 15.47% 5 0 3 3 3 : [çc|/a\|cç]: [//çcacç] 0.5 4 135.0 57.74% 5 0 2 3 4 : [ç|c/a\c|ç]: [//çcacç] 0.5 1 45.0 57.74% 5 1 2 3 4 : [ç|a/c\a|ç]: [//çacaç] 0.5 3 105.0 15.47% 5 1 3 3 3 : [ça|/c\|aç]: [//çacaç] 0.5 5 165.0 215.47% 5 1 1 3 5 : [|ça/c\aç|]: [//çacaç] __________________________________________________________________ |
|
| Red 16 |
0 0 0.00 9999.00 0 1 22.50 100.00 0 2 45.00 41.42 0 3 67.50 17.16 0 4 90.00 0.00 0 5 112.50 -17.16 0 6 135.00 -41.42 0 7 157.50 -100.00 ‒‒‒‒‒‒‒‒‒-
0.5 0 11.25 208.24 |
|
Otro caso complicado
 |
|
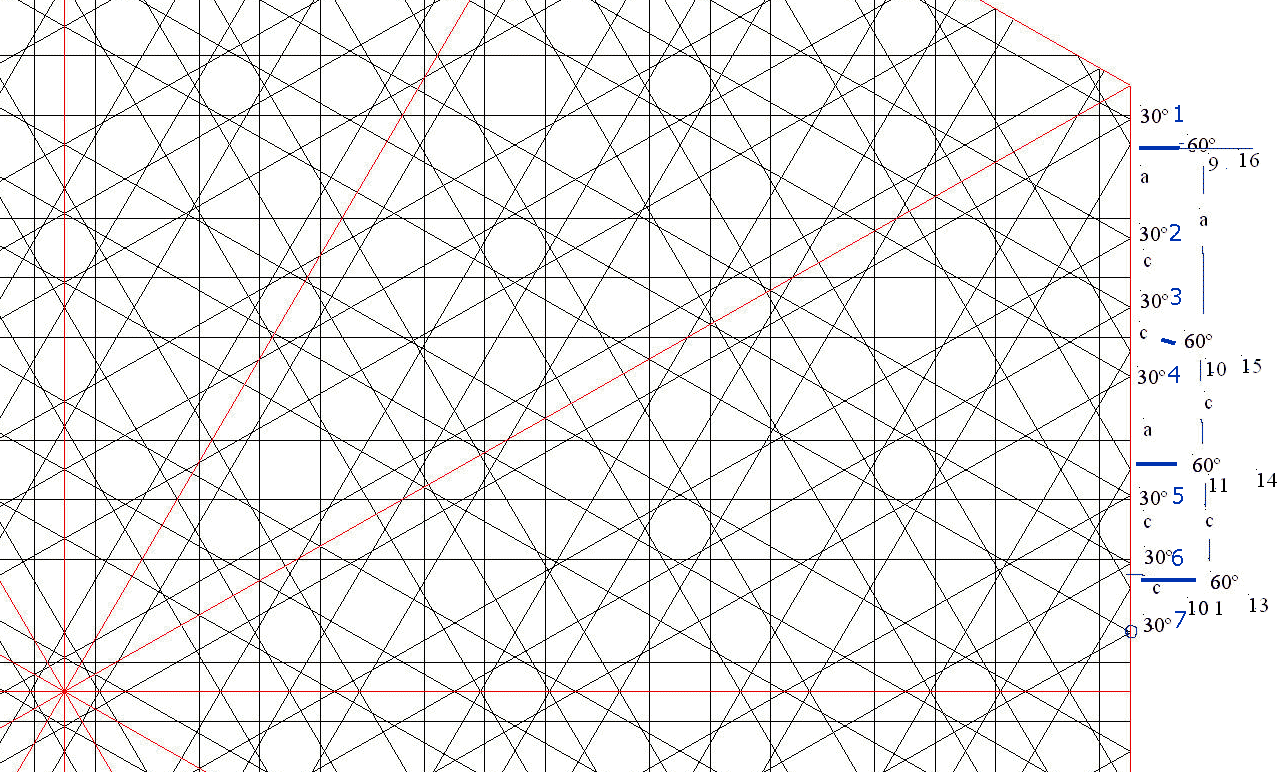
Red 12. X [//çaccaccacaccaccaç: 17] H [//çaccaccaccaccaç: 15]. sX[ 6a+ 10c ] sH[ 5a+ 9c ]. Dispos: dx=1. dy=0.87 dz=0.5 |
Esta red es empírica: Red 12.
H cumple [//çaccacc c ccaccaç: 15] la condición de 100% capicúa desde el centro. En la figura se aprecian, para alfa in=30º, los reflejos en vertical (desde arriba) las 7 primeras, ç acc acc, que se reflejan simétricamente, de manera capicúa, en las 7 últimas. Es decir, (en negrita y separado)
H [//çaccacc c ccaccaç: 15]
Así que parece que solo queda libre la central, que claro, no quebrantaría la simetría (aunque su valor es fijo, sumando de la proyección adecuada de X (regla1, ver más bajo). De modo que:
SS H debe ser simétrica (capicúa)
Pero X, ángulo 60º: çaccacca c accaccaç
Rn X , aparecen los pares de rayos a 60º ()ver figura) , separados por las distancias_
: 9-16, a 10-15 c 11-14 c 10-13
Es decir, se aparean (???) simétricamente en el sector marcado en negrita.
Red 12. X [//çaccacca c accacca ç: 17]
Esa sub-semi-secuencia (SSS) debe ser simétrica. ¡ Pero sólo ella.!
Lo cual quiere decir que las demás distancias son intercambiables permutables (lo que cambia su situación pero no la susu suma, es decir, las distancias que nos interesas, desde la 9º a la 16º. La 16, no importa porque cae fuera del sector vertical del eEGR.
Probémoslo, intercambiando al azar (no cambiando sin más , por4que ha de conservarse la condición de proyección, la regla 1ª: 1. Coeficientes de las combinaciones lineales de a y c en oblicuo X y recto H cumplen: En esta red 12, como se veía en Disegno empirico de redes de 12, es:
X[ 2ba+2gc ] ' = H[ ga+3bc ]. (1)
Y en efecto es periodica
Red 12. X [//acca çaccc accacca ç: 17] H [//çaccaccaccaccaç: 15]. sX[ 6a+ 10c ] sH[ 5a+ 9c ] Ss
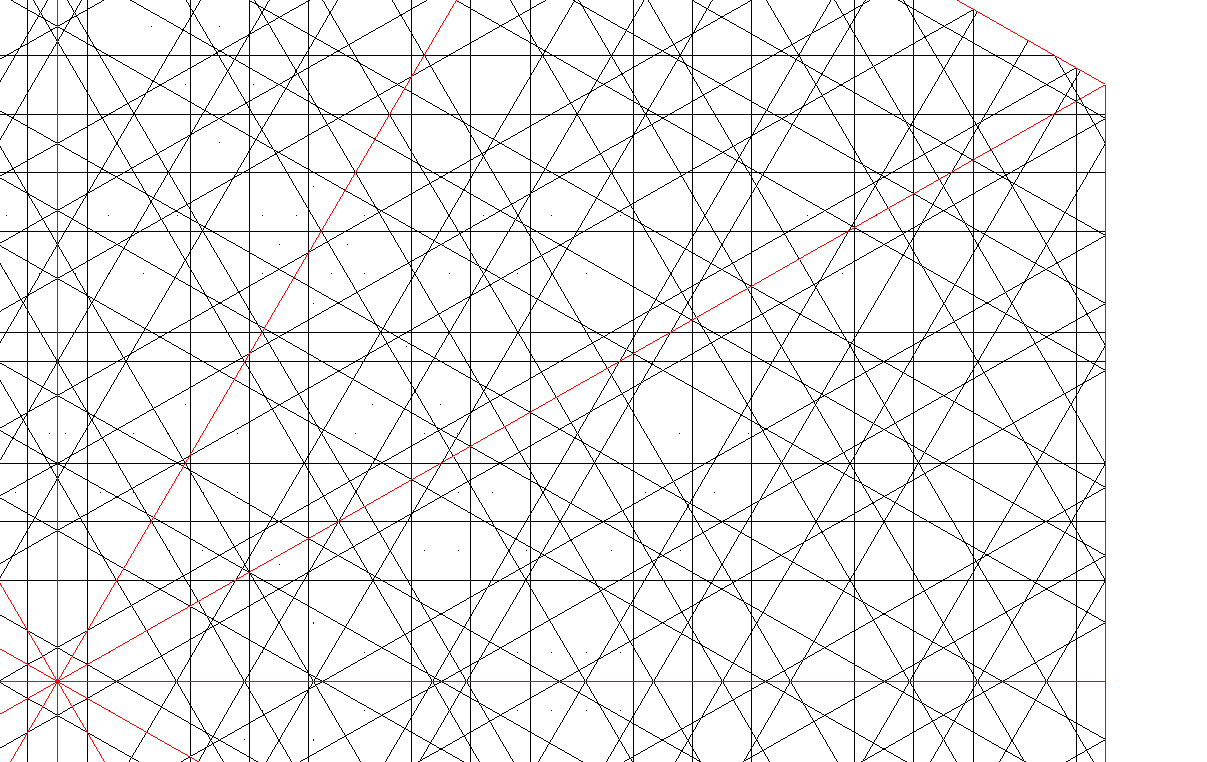
obtenida permutando las mitades de la parte libre de 1 a 8 en X. Véalo en figura 3.
 |
|
Red 12. X [//accaçacccaccaccaç: 17] H [//çaccaccaccaccaç: 15]. sX[ 6a+ 10c ] sH[ 5a+ 9c ] |
De modo que permutando arbitrariamente entre sí la parte no negrita y por otra parte, haciéndolo con la negrita y manteniendo su periodicidad, obtendremos redes periódicas de 12.
Estas condiciones son menos duras, más permisivas que las expuestas anteriormente, e
Disegno de redes de 12Puntos de reflejo.
Se observa que los puntos de reflejo en el la pared vertical se espacian diferentemente. A veces coinciden los de series (ángulos) diferentes) a veces no. Cabe preguntarse sobre la repercusión estética de esta distribución de puntos de reflejo, en el segmento vertical y en los demás. Incluso, al observan los círculos aparentes que aparecen dentro del triángulo EGR, que no son otra cosa que puntos de simetría radial mayor o menor, completa o incompleta, tenemos que preguntarnos sobre la elección de distancias, de las SS X y H, siempre dentro de la periodicidad elegida (recordamos que no es indispensable, cabe perfectamente una red no periódica, que se expande más u más hacia la periferia, sin bloques de desplazamiento.
Todo ello pretendemos estudiarlo en distribución de puntos de reflejo
Vuelta al Principio Última
actualización:
viernes, 18 de septiembre de 2015 Visitantes: