Disposición de bloques de red de 12 (perteneciente a Decoración Geométrica Islámica)
En nuestro Diseño de redes de 12 y en Redes periódicas de 12 buscábamos condiciones de las semisecuencias X y H pra ajustar las redes de bloques vecinos en una única red, para que las redes interiores sean parte de una misma red general de 12. Es decir, la misma, porque redes de 12 hay infinitas.
Pero este ajuste, esta coincidencia dependen de cómo se ajustan o disponen mutuamente los bloques, lo cual a su vez depender de la forma de este bloque.
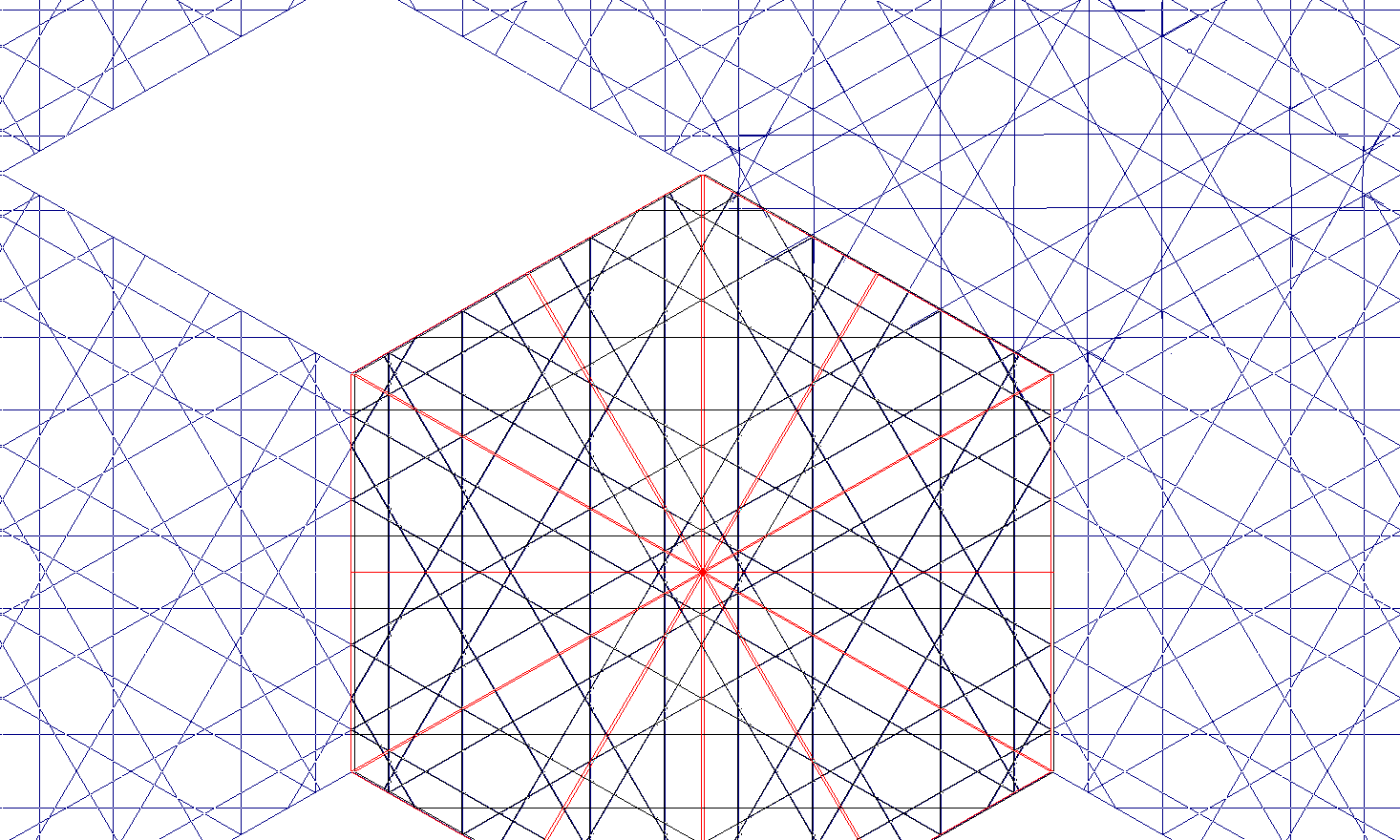
Para la forma hexagonal que hemos visto hasta ahora cabeb dos principales: en forma de ladrillos formando rectángulos en filas y columnas perpendiculares, o en forma de palan. SE comprueba la coincidencia de las redes dentro del bloque en una red general. Los huecos romboidales que esta disposición produce no violan esa comunidad de red, como comprobamos llenando manualmente el rombo superior derecho
 |
|
| Fig.1. Red 12 Oblicuo: X [//çacaç: 5] Recto: H [//çcacç: 5] sH[ 1a+ 3c ] sX[ 2a+ 2c ] Dispos: x=1. y=1.16 z=0. a/c= 1.73205080756888. SE rellena el hueco romboidal derecho superior a mano. El valor de y=1.16 es la separacion vertical igual a la horizontal, x, dividifa por cos(36º), 1(.86=1.16 |
En la figura 1 ajustamos los bloques adosándolos horizontalmente uno después del otro, es decir, desplazándolos un bloque, de modo que despla_x=1.
 |
|
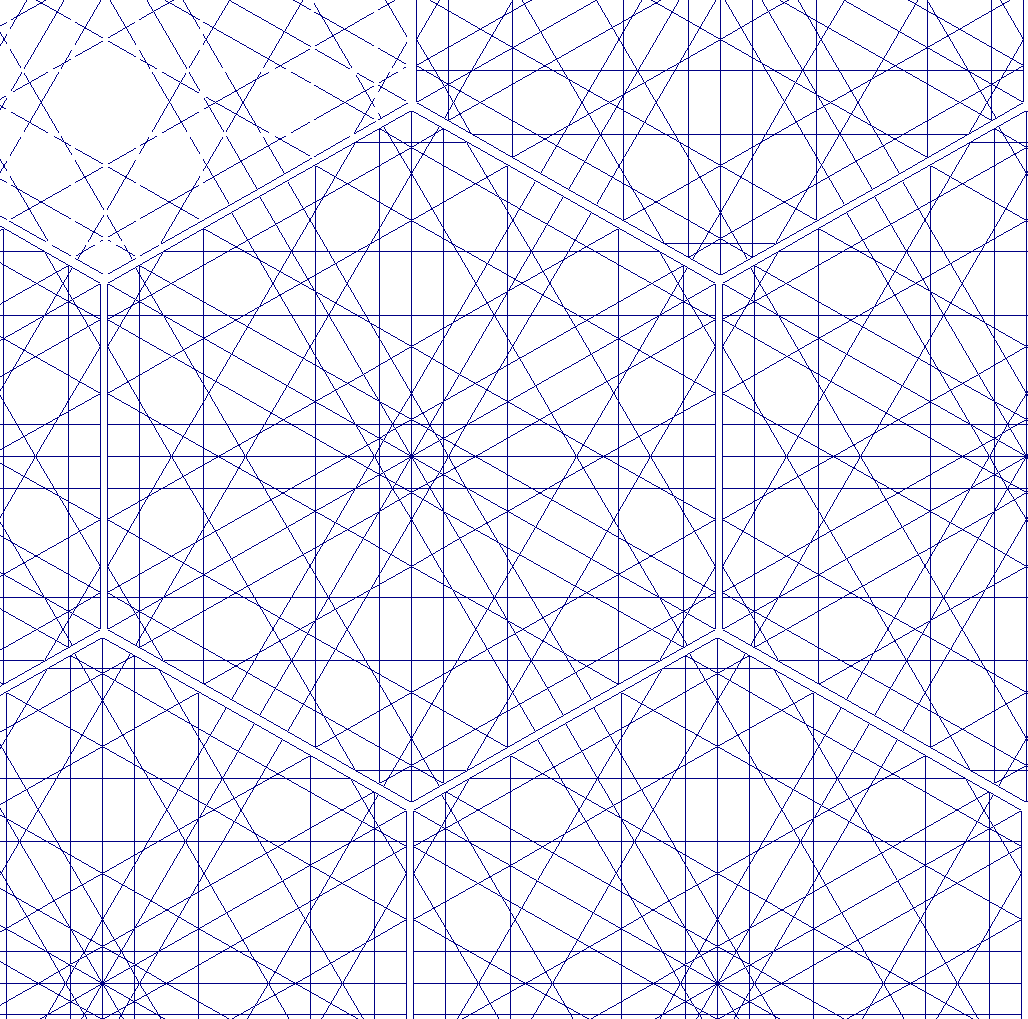
| Fig.2. Red 12 Oblicuo: X [//çacaç: 5] Recto: H [//çcacç: 5] sH[ 1a+ 3c ] sX[ 2a+ 2c ] Dispos: x=1. y=0.87 z=0.5 a/c= 1.73205080756888 |
En la figura ajustamos los bloques adosándolos horizontalmente uno después del otro, es decir, desplazándolos un bloque, de ahí, x=1.
Red 12 Oblicuo: X [//çacaç: 5] Recto: H [//çcacç: 5] sH[ 1a+ 3c ] sX[ 2a+ 2c ] Dispos: x=1. y=0.87 z=0.5
encintrábamos la falta de alguna consicion en las semisecuencias X y H para conseguir que la bloque de red de 12 genere la red de 12, o, en otras palabras,
que todas las rectas de la red que cortan el bloque coincidan con alguna recta del bloque.
lk bloque es aquí hexagonal, si usamos sólo dos series, X y H (cambiando enne, tendrámos un número diferente).
Se observan aquí dos tipos de rayo (segmento de recta de red dentro del bloque (que llamaremos desde ahora BR dentro del triangulo marcado en negro, el llamado por nosotros elemento generador de red, en adelante EGR. Así que el BR es n hexágono generado por el EGR mediante simetrías repetidas respecto a los ejes de simatría, en rojo.
Bien.
Primeramente se observan unosw rayos que incidene en otros simétricosa del EGR, y los que inciden en otro BR, al la der4echa. Tenemos pues tres series de intersecciones:
H: A B C D E F G H I 9 en total
V: J K L M N 5 en total
X : O P Q R S T U V X Y 10 en total
24 en total
 |
| Red 12 Oblicuo: X [//çacaç: 5] Recto: H [//çcacç: 5] sH[ 1a+ 3c ] sX[ 2a+ 2c ] a/c= 1.73205080756888 |
Observamos los siguientes propiedades de estas intersecciones o puntos aparentes de reflejo..
1. En todas ellas el rayo incidente y el reflejado forman igual ángulo con el límite
2. En H y X, los rayos i-r pertenecen a la misma semisecuencia e índice en ella. Por ejemplo:
Lim H: A(1h,1h), B(1h,1h), C(1h,1h), D(2h=2h), E(2x,2x), F(2h,2h), G(3h=3h), H(3x,3x), I(4h,4h), Lim X: Y(1x,1x), X(1h,1h), V(1x,1x), U(2h,2h), T(2x=2x), S(3x=3x), R(3h,3h), Q(2x,2x), P(4h,4h), Q(4x=4x),3. En V en cambio, pertenecen a la misma semisecuencia , X, pero distancias simétricas en la semisecuencia (de modo que la suma de sus índices es igual a su longitud, 5. Por ejemplo,
Lim V: J (1x=1x), K(2h, 2x), L (3x, 4x), M (1h,4x), N (2x=2x),
4. Se observan rayos aparentemente reflejados varias veces hasta que vuelven por mismo camino (al incidir perpendicularmente. Ejemplo,
Rayo 1: A X C M P I Rayo 2: Y B V J Rayo 3: D U F K R G Rayo 4: T E Q N Rayo 5: S H L OSon todos, los 24, porque seguir sólo encontraríamos los mismos rayor en sentido inverso.
De estos hechos empíricos
Diseño de redes hemos visto empíricamente las condiciones que deben cumplir las semisecuencias que definen el bloque de red para que al repetirse por translaciones vertical y horizontal se genere una red única en la que todos los bloques quedan colocados, es decir, sus rectas de red coinciden con las de la red general.
Veamos en detalle la justificación de esas reglas, una en realidad:
la semisecuencia oblicua debe ser capicúa
como la de la figura, que es: X [//çaacaaç: 7]: . Siete elementos pues, siete distancias que podemos ver en la figura.
En ella encontramos los puntos A, B y C en la periferia ‒en rojo.‒ vertical derecha del bloque de red.
Vemos que en esos puntos concurren, son generados por, dos rectas oblicuas con ángulos de 45º y 135º. Su ordenación desde sus ejes de simetría , escritos dentro son
A, 6 - 1 B, 5 - 2 C, 4 - 3
o sea suman en todos los casos 7, la longitud de la semisecuencia.
Geométricamente eso significa que las suma de los segmentos de cada par de rectas dentro del bloque es constante, o, lo que que equivale, también es constante la suma de los segmentos concurrentes dentro del triángulo en rojo limitado por la horizontal central, diagonal de 45º y la vertical a la derecha, lo que llamamos elemento generador de red. Nombre justificado porque por simetrías repetidas respecto a los ejes de simetría, en rojo, qu no pertenecen a la red, se ge
RED 8 Recto: H [çacç: 4] Oblicuo: X [çcaaç: 5]
La situación se repite en el triángulo simétrico al generador respecto a la bisectriz principal, con los puntos homólogos A', B', C' y en los demás simétricos con los tríos A",B",C";A"', B"', C"' y así sucesivamente hasta 8 veces..
La no constancia de esa suma, igual a la longitid de la semibisectriz principal, conduce al caso 3º, en que la red interior no genera la exterior.
Se ven estas redes periódicas en Catálogo de redes 8.y se compriuba en todas el cumplimiento de la condición encontrada.
Vuelta al Principio Última
actualización:
viernes, 18 de septiembre de 2015 Visitantes: