Diseño de redes de 10 (perteneciente a Decoración Geométrica Islámica)
Hemos visto las redes
periódicas de 8, en Diseño de redes de 8, en
Diseño empírico de
redes de 12 y Redes
periódicas de 12. Repitamos el estudio para 10; no será tan sencillo,
porque R10 es más compleja (y misteriosa) que las dos anteriores. Nos
referimos, claro, a la proporción de oro, o áurea, que aparece continuamente en ella.
Comprobemos ahora la relación entre estos ángulos y la proporción entre sus segmentos. En el triángulo de la figura, isósceles, con dos ángulos de 72º y uno de 36º se verifica a/c =c/d. Pero a = d + c
Luego: a/c = c / (a-c), con lo que:
a/c = (1+√5 )/2 = 1. 610
(el signo negativo daría lugar a un segmento de longitud negativa, que despreciamos).
Escribamos primero una tabla de las razones trigonométricas de p /5 y sus primeros múltiplos y submúltiplos. Aparecen estos valores áureos, .618 y 1.618.
| Ángulo | seno | 2 seno | coseno | 2 coseno | tangente | 2 tangente | |
| 2p /5 | 72º | .951 | 1.902 | .309 | .618 | 3.079 | 6.155 |
| 2p /10 | 36º | .588 | 1.176 | .809 | 1.618 | .727 | 1.453 |
| 2p /20 | 18º | .309 | .618 | .951 | 1.902 | .325 | .649 |
Las relaciones entre vectores de base (separaciones entre paralelas) han cambiado: primeramente la relación a/c, que es ahora
a/c =2.cos(2p / 10) = 2.cos(p /5) = 2.cos(36º)=2.((√5 +1)/4) = 1.610...
La proyección de las distancias en oblicuo sobre el recto son ahora (recordamos que la vírgula o comilla significa aquí proyección):
a'=a.cos(2p/10)=((1+√5 )/2)+(1+√5 )/4)=(1+5+2√5)/8=(3+√5)/4=2/4+(1+√5)/4=c/2+a/2
c'=c.cos(2p/10)=(1+√5 )/4=a/2
Así,
(2a) ' = c + a (2c) ' = a (1)
Luego disponiendo de cualquier combinación (coeficientes pares) del par de distancias a y c en la semisecuencia oblicua X, debe cumplirse
X [2ba+2g c ] ' = H [(g + b) a+b c ] (2)
entre rectas paralelas a esas direcciones. Si ahora llamamos ç =c/2 y a¿ =a/2, podemos también proyectar combinaciones lineales de esas mitades de separaciones básicas, aun manteniendo que en la red sólo aparecerán las separaciones enteras originales. ¿Cómo es eso?. Porque siempre podemos asociar dos a dos las mitades de cada separación base, componiendo enteras. Si son pares el número de mitades, ya tenemos las separaciones enteras. Si son impares, la que sobre de los pares se coloca en un extremo: componiéndola con su simétrica al otro lado del eje de tenemos la separación entera. Si también aparece una mitad non de la otra separación, la colocamos al otro extremo de la semicescuencia, junto al eje de simetría pues, componiendo con la mitad non al otro lado, la separación completa.
Así que consideraremos combinaciones lineales de mitades de separación, las citadas ç =c/2 y a¿ =a/2,
Todo esto nos ha sedo sugerido por el estudio empírico de redes de 10 disponiendo los BDR de modo que coincidan la mayoría de sus rayos en BDR diferentes. Ello no ha sido posible y siempre hay uno que se va desplazando, por decirlo, así a medida que cambio de fila de BDR. Veamos la figura, encontrada, insistimos, empíricamente, probando, que nos sugiere métodos de análisis y desarrollo.
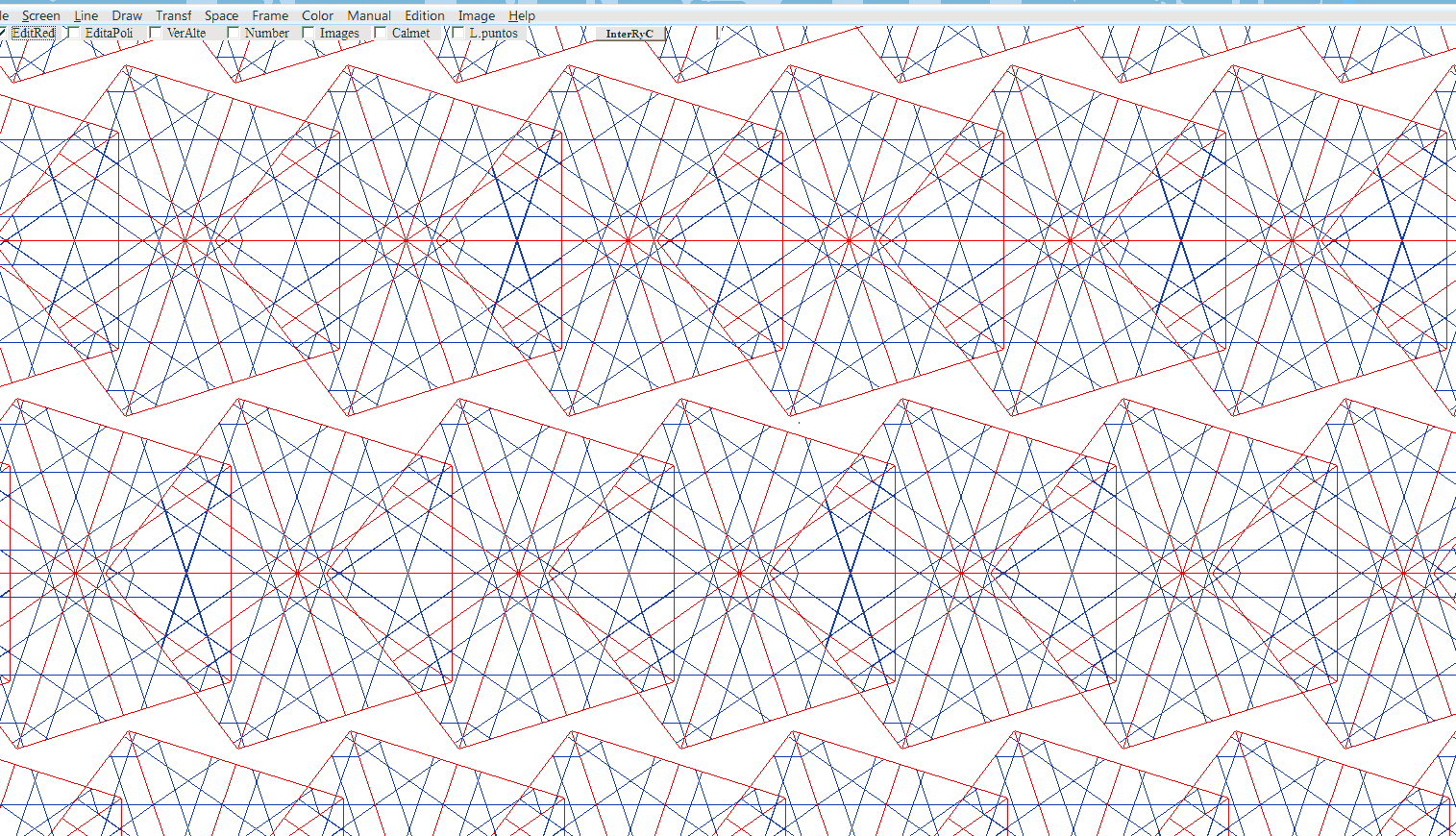
donde disponemos los pentágonos de 10 ejes en filas, desplazándolas de modo que se configuren triángulos isósceles como los de la figura 1.
También podemos girar 18º (medio Beta) a la izquierda, encontrando una ordenación de tipo tradiciona, filas sin desplazamiento relativo, como ladrillos colocados en filas y columnas regulares.
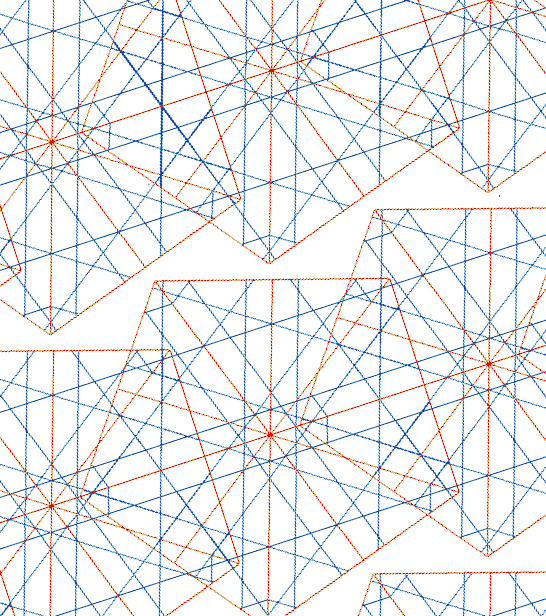
Vea casos reales, construidos, en Red10-Kayseri.
Vuelta al Principio Última
actualización:
Wednesday, 31 de July de 2013 Visitantes: