 En la figura se ve e
En la figura se ve e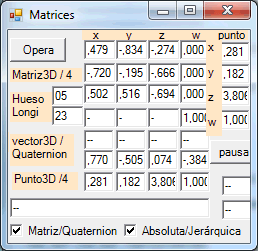 n
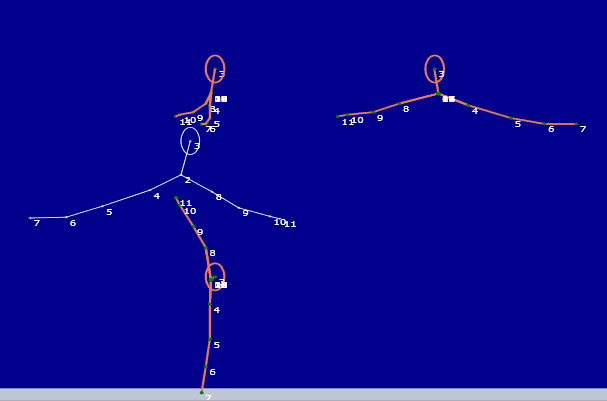
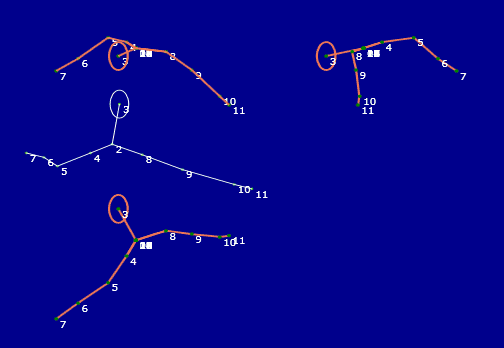
blanco el esqueleto original; y en naranja las tres vistas habituales del dibujo técnico, alzado a la izquierda,
encima del anterior; planta
debajo de este último, vista lateral al derecha.
Peso a la poca visibilidad de los
gráficos, puede apreciarse que lo que debe ser el alzado, se le como una
vista de planta, hecho confirmado por la propia
planta de este dibujo que aparece con el aspecto del alzado original (en
blanco), de pie, pero torcido, inclinado a la izquierda en el dibujo.
Esto quiere decir que el esqueleto
original ha sufrido una transformación que describimos como:
1. Giro del esqueleto hacia atrás
con respecto al línea de los hombros. como eje. El esqueleto bascula
hacia atrás.
2. Sobre este esqueleto basculado
se rota ahora, con eje vertical yendo la cabeza hacia la izquierda
del dibujo, y los pies hacia la derecha.
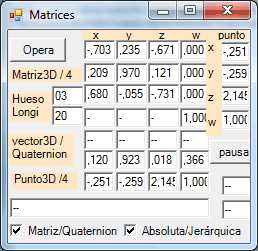
La transformación realizada se ha
conseguido usando una matriz arbitraria: la matriz de rotación absoluta
de la articulación 5, el codo derecho. Sus valores aparecen en la parte
superior del segundo grafico. Asimismo aparece el quaternion
correspondiente a la matriz citada, el hueso elegido como referencia y
su longitud. El punto, escrito en horizontal y vertical en uno de los
operados o transformados.
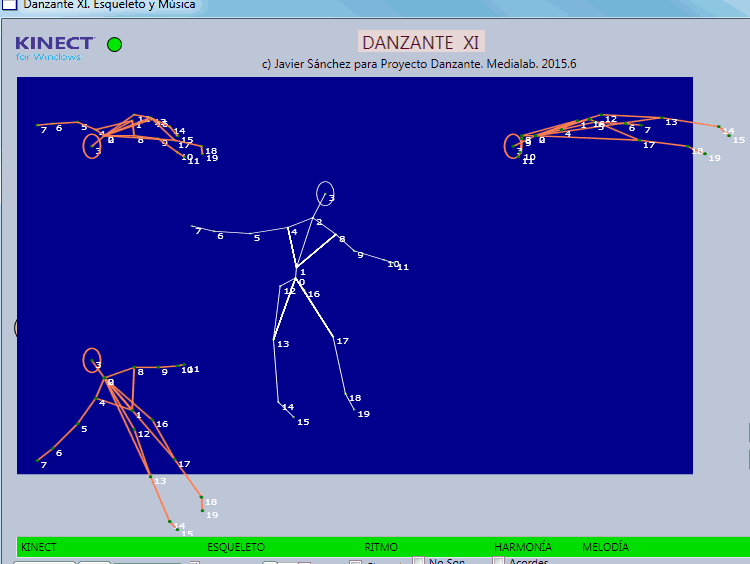
Veamos ahora un dibujo más claro
de interpretar geométricamente.
n
blanco el esqueleto original; y en naranja las tres vistas habituales del dibujo técnico, alzado a la izquierda,
encima del anterior; planta
debajo de este último, vista lateral al derecha.
Peso a la poca visibilidad de los
gráficos, puede apreciarse que lo que debe ser el alzado, se le como una
vista de planta, hecho confirmado por la propia
planta de este dibujo que aparece con el aspecto del alzado original (en
blanco), de pie, pero torcido, inclinado a la izquierda en el dibujo.
Esto quiere decir que el esqueleto
original ha sufrido una transformación que describimos como:
1. Giro del esqueleto hacia atrás
con respecto al línea de los hombros. como eje. El esqueleto bascula
hacia atrás.
2. Sobre este esqueleto basculado
se rota ahora, con eje vertical yendo la cabeza hacia la izquierda
del dibujo, y los pies hacia la derecha.
La transformación realizada se ha
conseguido usando una matriz arbitraria: la matriz de rotación absoluta
de la articulación 5, el codo derecho. Sus valores aparecen en la parte
superior del segundo grafico. Asimismo aparece el quaternion
correspondiente a la matriz citada, el hueso elegido como referencia y
su longitud. El punto, escrito en horizontal y vertical en uno de los
operados o transformados.
Veamos ahora un dibujo más claro
de interpretar geométricamente.
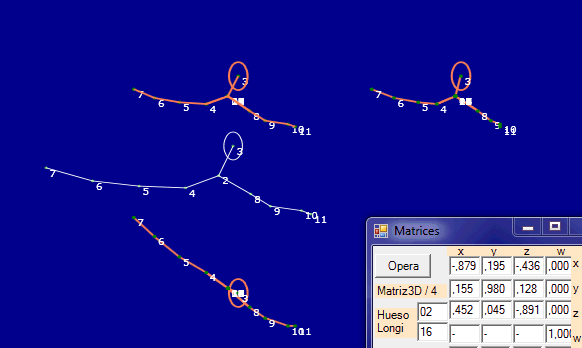
 Observamos un movimiento similar
al descrito para el primer gráfico, pues hemos empleado ella
articulación 5
La transformación se efectúa
mediante las siguientes líneas de código fuente, en VisualBasic 10 :
Observamos un movimiento similar
al descrito para el primer gráfico, pues hemos empleado ella
articulación 5
La transformación se efectúa
mediante las siguientes líneas de código fuente, en VisualBasic 10 :
Cambiando la articulación y su matris, la empleada para transformar todo el esqueleto, en concreto la articulación 3 (cabeza) encontramos una rotación diferente:
' Public transforma_matriz As Byte = 1 'transforma esqueleto mediante matriz (1) o quaternion (0) ' Public transforma_absoluta As Byte = 1 'transforma esqueleto mediante matriz o quaternion absolutos (1) o jerarquicos (0) 'TODO GIRO EXIGE llevarlo al origen = referirlo a referencia interna o solidario (hombros) 'girar y llevar a su sitio 'TRANSLACION() no pide esos desplazamientos '1. Llevo al origen punto_fini4 = punto_fini4 - punto_refe4 '2. transformo If transforma_matriz = 0 Then punto_fini3 = punto_fini3 - punto_refe3'rota la matriz, no el punto; este es el centro de giro matriz.RotateAt(cuaternion, punto_fini3) punto_fini4 = punto_fini3 End If punto_fini4 = matriz.Transform(punto_fini4) 'reduccion por si acaso se desmanda el dibujo punto_fini4.X = punto_fini4.X / 2 '- 0.3 punto_fini4.Y = punto_fini4.Y / 2 '- 0.3 '3. devuelvo al punto en que estaba punto_fini4 = punto_fini4 + punto_refe4