Esta página está en construcción: perdonen los errores y temas inacabados.
This page is being developed: I am sorry for errors and unfinished subjects.
Recubrimiento del plano (perteneciente a Decoración Geométrica Islámica)
Todas las Riges recubren el plano, es decir, las piezas que la componen, colocadas adecuadamente, coinciden en sus bordes de modo que podemos pasar siempre de una a otra: sus bordes, aristas, segmentos rectos, coinciden. Excluimos las tiras que separan como fronteras con grosor esas figuras elementales.
El tema viene de antiguo, porque siempre hubo pavimentos que se realizaban con piezas iguales o con un pequeño número de piezas iguales. esas son nuestras baldosas que han llegado a una regularidad monótona en su forma cuadrada.
Como estrategia general podemos considerar los vértices o los polígonos. Comenzamos por los primeros.
Regulares
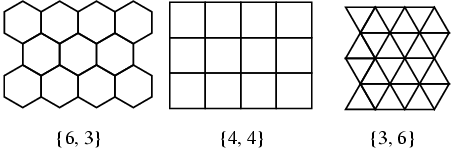
Partiendo de lo más regular, contamos con los pavimentos (llamémoslos así) de baldosas en forma de polígono regular dispuestas de modo que coincidan sus lados: así que estos son iguales. Las llamaremos pavimentos regulares equiláteros (si se renuncia a esa equilatelaridad podemos encontrar infinitos recubrimientos: por ejemplo, baldosas cuadradas de cualquier tamaño).
Encontramos en internet (en mathworld.wolfram.com/tessellation, aunque es tan simple que debíamos haberla encontrado nosotros) la fórmula que, expresando que q ángulos (iguales) de polígono regular de p lados y ángulos coinciden en un vértice cubriendo el plano exactamente (no recubriéndolo) o sea, suman 360º o 2p radianes:
q ( p (p-2) / p) = 2p (1)
lo que conduce a
(p-2) (q-2) = 4 p, q > 2 (2)
o
(1/2 - 1/p) (1/2 - 1/q) = 1 p, q > 2 (2')
que permite, sabiendo que tanto p como q son enteros, probar hasta encontrar todas las soluciones, que son
| Pavimento | p | q | {p,q} |
| Triángulos | 3 | 6 | {3,6} |
| Cuadrados | 4 | 4 | {4,4} |
| Hexágonos | 6 | 3 | {6,3} |
y no hay más porque no hay polígonos de 2 lados y ángulos llanos en nuestros polígonos. El código {p,q} es llamado Schläfli.
Nótese que p y q son hasta cierto punto competidores: cuanto mayor es p, mayor el el ángulo interior de un polígono y por lo tanto menos (menos q) cooperan en un vértice par cubrir el plano. Su producto o suma o función relacionada con ellas tenderá a ser constante. Eso precisamente expresa la ecuación (2), la cual puede también ser expresada como
1/ p + 1/q = 1/2 p, q > 2 (3)
que evidentemente es verificada por el cuadro. Esta forma es interesante porque para poliedros regulares (solidos con polígonos regulares por caras( se verifica
1/ p + 1/q < 1/2 p, q > 2 (3')
así que el recubrimiento plano resulta ser el poliedro extremo, el límite de 'planidad', empleando un horrible neologismo.
Semirregulares (2 tipos)
Si admitimos más de un polígono en nuestros pavimentos (siempre regulares) tenemos más posibilidades: para dos tipos, nuestra ecuación inicial deviene ahora, recordando que en un vértice van a coincidir q1 ángulos de polígono de p1 lados y q2 ángulos de polígono de p2 lados, sumando como antes 4 rectos, o sea, 2p . El código será ahora { p1 ; p2 , q1 ; q2 }
q1 ( p ( p1 - 2 ) / p1 ) + q2 ( p ( p2 - 2 ) / p2 ) = 2p (4)
lo que conduce a
q1 ( 1/2 - 1 / p1 ) + q2 ( 1/2 - 1 / p2 ) = 1 (5)
o bien
p2 q1 ( p1 - 2 ) + p1 q2 ( p2 - 2 ) = 2 p1 p2 (6)
con q1 , p1 , q2 , p2 enteros positivos y p1, p2>2
que intentamos poner en la forma de (3'):
q1 (1/2 - 1/p1 ) + q2 ( 1/2 - 1/p2 ) = 1 (6')
con q1 , p1 , q2 , p2 enteros positivos y p1, p2>2
ahora tenemos más `posibilidades y valores más altos: Calculando con un límite superior para todos los parámetros en 12, obtenemos 20 posibilidades, en el cuadro siguiente (cuyas numeraciones no coinciden todavía con las que figuran en los dibujos):
1. { 3 ; 12 , 1 ; 2 } |
6. { 6 ; 3 , 1 ; 4 } |
|
16. { 4 ; 4 , 3 ; 1 } |
Los casos en que p1 y p2 son iguales son los considerados antes, y aparecen en el gráfico siguiente con los números equivalentes 3 y 8 para el primero; 5, 12 y 16 el segundo; y 15 , 18 y 20 el tercero. Nos quedan 20-5 = 15 más.
|
|
| Fig. 1 |
1. { 3 ; 12 , 1 ; 2 } |
|
|
| Fig. 9 |
Aparecen en el siguiente gráfico 8, que corresponden a nuestros casos 13, (el siguiente tiene 3 polígonos), 9, 14 (y 17), 1 (y 10), 14 (y 17), (el siguiente tiene 3 polígonos), y 6 (y 19). Excluidos los citados nos quedan 15- 8 = 7. ¿Cuales son?
2. { 4 ; 8 , 1 ; 2 }
4. { 10 ; 5 , 1 ; 2 }
7. { 5 ; 10 , 2 ; 1 }
11. { 3 ; 6 , 2 ; 2 }
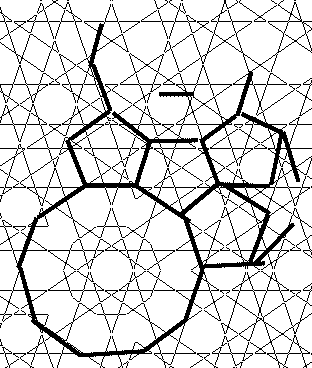
El primero sugiere 1 cuadrado rodeado de 2 octógonos. Es como el caso 9, que se nos pasó. Quedan 3. El último es igual al 13, ya excluido, que se nos pasó también. Quedan dos, equivalentes, constituidos al parecer por decágonos y pentágonos. Interesantes.
Ambos casos recetan un decágono coincidiendo en sus vértices con dos pentágonos. Es caso es posible en efecto, porque 8/10 + 6/5 vale en efecto 1.
Ahora bien ¿cubrimos el plano con estas uniones? Pues no, porque tras rodear el decágono de pentágonos, 10 de ellos, hay que seguir cubriendo y nos encontramos con que en un momento coinciden en un vértice tres pentágonos que no cubren, falta una esquina (de 36º) que podía únicamente resolverse con una estrella de cinco puntas, el pentáculo. Son tres figuras, caso excluido antes y además estrellada, tampoco considerado.
Es claro que hacen falta más ecuaciones o condiciones para encontrar todas y sólo ellas, las redes semirregulares posibles.
Sólo hay (hemos intentado hasta polígonos de 64 lados) los seis casos ya vistos
|
|
| Fig. 10 |
1. { 4 ; 3 , 2 ; 3 } |
siendo el primero solución de dos colocaciones, la 4ª y 6ª en el dibujo segundo, llamados pavimentos del Cairo (?). Escribimos bajo cada uno su código (deducido del Schläfli para regulares.)
Se ve que necesitamos más condiciones para hallar pavimentos, que desechen casos como el de las redes de 5 antes considerado. Desechada como pavimento semirregular, porque ya se apuntó que era una interesante solución. En particular todos los vértices deben cumplir la solución citada. Si se dan vértices dcon diferente composición, diferentes polígonos concurrentes, entramos en redes más libres.
Semirregulares (3 o más tipos)
Para 3 o más, n, polígonos diferentes que se reúnen necesariamente en todos los vértices, obtenemos la ecuación necesaria (pero no suficiente como vimos para n =2 .
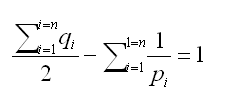 (7)
(7)
Probando para 3 tipos, obtenemos:
| 3 | 3,4,6 | otros |
|
1: 3; 3; 3 , 1; 1; 4 ; 2: 3; 3; 3 , 1; 2; 3 ; 3: 3; 3; 3 , 1; 3; 2 ; 4: 3; 3; 3 , 2; 1; 3 ; 5: 3; 3; 3 , 2; 2; 2 ; 6: 3; 3; 3 , 2; 3; 1 ; 7: 3; 3; 3 , 3; 1; 2 ; 8: 3; 3; 3 , 3; 2; 1 ; |
9: 4; 3; 3 , 2;
1; 2 ; 10: 4; 3; 3 , 2; 2; 1 ; 11: 4; 4; 3 , 1; 1; 3 ; 12: 4; 4; 4 , 1; 1; 2 ; 13: 4; 4; 4 , 1; 2; 1 ; 14: 4; 4; 4 , 2; 1; 1 ; 15: 6; 3; 3 , 1; 1; 3 ; 16: 6; 3; 3 , 1; 2; 2 ; 17: 6; 3; 3 , 1; 3; 1 ; 18: 6; 4; 3 , 1; 2; 1 ; 19: 6; 6; 3 , 1; 1; 2 ; 20: 6; 6; 6 , 1; 1; 1 ; |
21: 8; 8; 4 , 1; 1; 1 ; 22: 10; 5; 5 , 1; 1; 1 ; 23: 12; 4; 3 , 1; 1; 2 ; 24: 12; 6; 4 , 1; 1; 1 ; 25: 12; 12; 3 , 1; 1; 1 ; 26: 15; 10; 3 , 1; 1; 1 ; 27: 18; 9; 3 , 1; 1; 1 ; 28: 20; 5; 4 , 1; 1; 1 ; |
Aquellos con los tres polígonos iguales son las redes regulares, naturalmente, vistas en primer lugar. Si sólo hay dos valores se trata de las semirregulares vistas antes también. Respecto a las demás, que son únicamente los seis últimos, aparecen aquí ya los excluidos en el gráfico anterior, el primero con el nº. 23. {12; 4; 3 , 1; 1; 2 }; el segundo con el nº 24: {12; 6; 4 , 1; 1; 1 }. Excluyendo los de orden inferior:
1: { 6; 4; 3 , 1; 2; 1 } |
los anteriores son ahora 1 y 3; estudiaremos los demás: vaya primero otra de las figuras de las llamadas demirregulares:
|
|
| Fig. 11 |
Relacionado con lo anterior:
Veamos cómo aplicamos estas redes, sobre todo las regulares, para recubrir el plano mediante nuestras Riges en recubrimiento del plano: módulo de traslación.
Veamos enlosados varios.
(seguirá)
Vuelta al Principio Última
actualización :
domingo, 12 de agosto de 2018
Visitantes: