Esta página está en construcción: perdonen los errores, repeticiones y temas inacabados.
This page is being developed: I am sorry for errors, duplications and unfinished subjects.
Euler:_caras_aristas_vertices
C + V = A + 2
La sencilla pero algo misteriosa ecuación que liga el número de caras en un poliedro (cuerpo o figura en tres dimensiones limitado por polígonos que se unen dos a dos en las aristas, y de q en q en los vértices ) puede aplicarse a cualquier figura plana que cumpla esas condiciones pero en el plano. El cerramiento posterior que todo cuerpo compacto, con interior y exterior, tiene, es realizado en el plano con la parte del plano exterior a la red de polígonos. Es como si rodeara la tierra por detrás. Se parece (es esencialmente lo mismo) a un mapa (el político, el de los países).
Inventamos un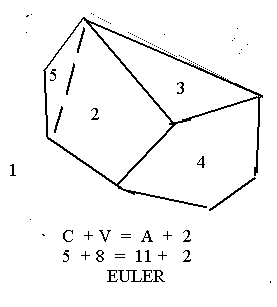
a demostración, la cual, como casi todo lo que inventamos,
estaba ya inventado.
Elijamos un polígono cualquiera: tiene p lados (o aristas) y p vértices (5 de cada en el dibujo) ; de modo que contando el polígono y su exterior como dos caras, tenemos que se cumple C+V=2+p A+2 =2+p: C+V=A+2 , pues, que reescribimos como C-V-A=2.
Ahora comprobemos que adosando nuevos polígonos al inicial (que P2, ya que el primero, P1, es el exterior) se nos conserva la fórmula, porque los aumentos se van compensando mutuamente:
Adosando el polígono P3 al P2 por una arista, observamos que añadimos 2 aristas y 1 vértice, es decir ( si p3 es el número de lados y ángulos del polígono P3), P3 - 1 que es 2, por ser P3 un triángulo. Y aumentamos también 1 vértice, es decir, P3 - 2; como hemos aumentado también el número de caras a 3, tenemos que C+V-A = 3 + 5 - 6 = 2, o en general :
3 + (p3 - 2 )-(p3 - 1 ).
Es decir
el aumento de 1 cara se compensa con el aumento, menor en 1, de los vértices respecto a las aristas
y esto
con independencia del número de lados del nuevo polígono.
Y con independencia también del número de aristas que adoso con él. Por ejemplo, P4, un pentágono que adosa el conjunto P2-P3 en 2 aristas, añade igualmente p4 - 2 aristas y p4 -3 vértices, que son los que se adosan y que estaban ya contados, por lo tanto.
En general todo nuevo polígono Pi, de pi lados y vértices, adosado en si aristas, añade 1 cara, pi-s aristas y pi-s-1 vértices. Luego el aumento es nulo: 1 + (pi-s-1)-(pi-s) = 0
Si creo un nuevo polígono uniendo dos vértices de uno antiguo, no añado vértices y añado una cara y una arista: compensación igualmente. Luego:
Para toda figura plana o espacial (porque todos los razonamientos carecen de limitaciones en las direcciones de aristas y caras) compuesta de polígonos irregulares o no adyacentes dos a dos por un lado, cumple la ecuación de Euler que aparece en nuestro frontispicio, con todos los honores.
Esto lo cumplen hasta los polígonos degenerados: Ángulo: 1+3=2+2. Segmento: 1+2=1+2 Punto: 1+1=0+2 Nada: Aquí falla
Es particular nos interesan nuestras Riges (redes islámicas geométrica entrelazada) porque recubren el plano.
Cualquier conjunto de rectas o curvas que se cortan cumple también la fórmula, siempre que se comporten como mapas, la versión curva de nuestra red poligonal.
Vuelta al Principio Última
actualización:
domingo, 12 de agosto de 2018 Visitantes: