Rozamiento de aire a flecha I (forma parte de Arquería )

Nos referimos en esta página a rozamiento longitudinal, el que ejerce el aire al avance de la flecha, la cual adoptará la posición tangente a la trayectoria.

Para rozamientos laterales, vea Rozamiento lateral de aire a flecha.

Traemos y ampliamos estas ecuaciones de la trayectoria de la flecha desde anteproyecto modelo de arco. Son ecuaciones originales, obtenidas por integración directa por nosotros.

La aceleración según el camino de la trayectoria, --llamada aquí vector s--, tangente pues a la misma es:

s" = ‑ g ‑ k₀.s'

siendo s', s" las derivadas primera y segunda del camino s, es decir, su velocidad y su aceleración, y g el vector gravedad. k es un factor de resistencia dependiente del rozamiento de la flecha con el aire, que compone una aceleración negativa, deceleración, al multiplicar a la velocidad de la flecha. Rozamiento pues proporcional a la velocidad de la flecha con un un factor de proporcionalidad k.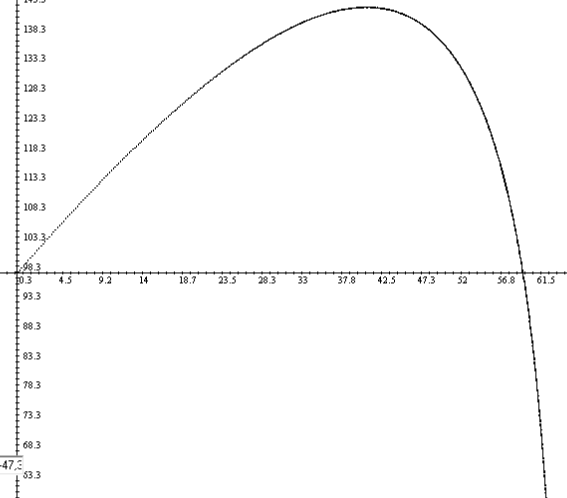

Proyectando las aceleraciones sobre los ejes x e y, multiplicando por la masa de la flecha, y llamando k al al cociente k₀/g tenemos las ecuaciones correspondientes de las fuerzas que operan sobre la flecha durante su vuelo:

m.y" = ‑ m.g ‑ k.y'

m.x" = ‑ k.x'

El factor de rozamiento nos es desconocido. pero podemos admitir algunas variables que le condicionan (de las que depende): en principio depende del área del perpendicular a la trayectoria que opone al camino de la flecha, como un remo ancho resulta más efectivo. Y una vela grande remolca un barco con más fuerza.. Podemos suponer que cuanto más fina es la flecha, menor es el rozamiento al avnace. A su vez la presencia habitual de plumas o similares ofrecerá una rozamiento adicional. Puede pensarse que este rozamiento es perjudicial para el vuelo citado. pero hay que recordar que esas plumas pueden ayudar, incluso ser indispensables para el vuelo en condiciones no ideales (viento, enderezamiento del la flecha tras una desviación cualquiera).

Integrando de manera inmediata estas dos ecuaciones diferenciales se obtienen fácilmente las ecuaciones paramétricas de la trayectoria:

u_e (u₀ + u_e ) ‑ (gt/u_e )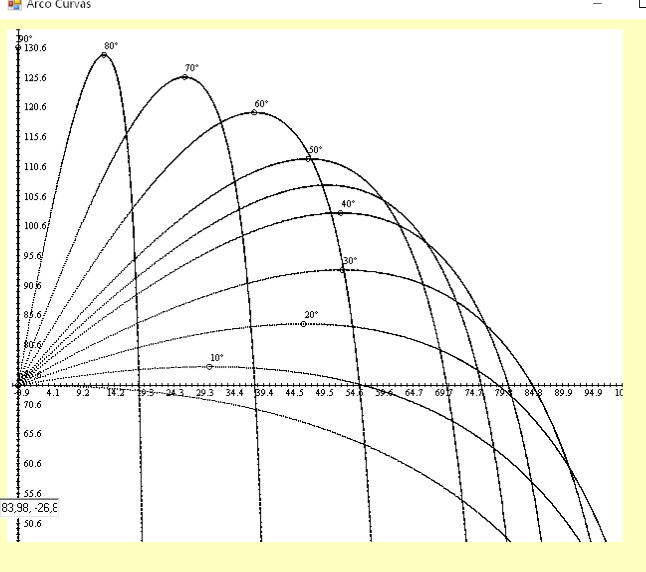

y = ‑‑‑‑‑‑‑‑‑‑–––– . ( 1 ‑ e ) ‑ u_e .t

u_e .w₀ ‑ (gt/u_e )

x = -‑‑‑‑‑- . ( 1 ‑ e )

de las que se obtienen las coordenadas del punto x, y en el instante t, de una flecha que sale con velocidad v₀ y un ángulo a con la horizontal;

De ellas puede obtenerse fácilmente la ecuación de la altura de la flecha en cada punto del camino en el suelo:

(REVISAR)

u₀ + u_e

y = ‑‑‑‑–––– . x + ( u_e² / _g ) . ln [ 1 - (^g/ u_e.w₀) . x ]

w₀

u0 y w0 son las proyecciones de esa velocidad sobre los ejes vertical y horizontal, o sea:

u₀ = v₀. sen(a ) w₀= v₀. cos(a ) u_e es un parámetro dependiente de la masa de la flecha y del coeficiente k de rozamiento, de expresión: u_e = m.g / k que resulta ser la llamada velocidad límite, o sea la que alcanzaría la flecha dejándola caer verticalmente. g es la aceleración de la gravedad. Las dimensiones de k (= m.g/u_e ) son las de fuerza/velocidad (M L^-2 (L/T)^-1) Véase en la figura adjunt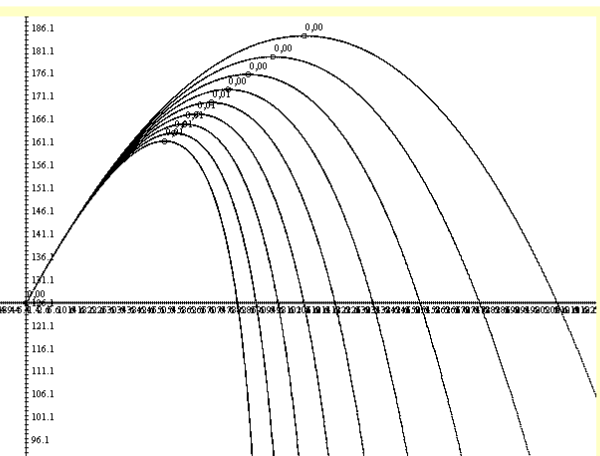

a la trayectorias con las constantes:

'CONSTANTES

alfa_fle = 45º 'angulo de salida

masa_fle = 0.025 'gramos a kilos

velo_ini = 50 'm/s

grave = 9.8 'm/s2

kroza = 0.01 'a ver sus dimensiones

Pueden verse algunos datos en Velocidad de la flecha_ medidas reales.

Y ahora véanse en la figura siguiente las trayectorias cambiando el ángulo de salida de la flecha; nótense sus formas y alcances diferentes. Por ejemplo, con ángulo inicial de 10º se alcanzan unos 50 metros y se sube hasta 5 aproximadamente. El máximo alcance, unos 84 metros, se logra con unos 30º, alzándose la flecha hasta unos 95 metros. La máxima altura se logra, lógicamente con un ángulo de 90º (¡mucha precaución con este tiro!)

Para otro rozamiento, todos estos datos varían. Vea la familia de trayectorias para diferentes rozamientos:

Valores

Familia -ángulos salida (Valores MKS)

kroz alfa_fle masa_fle velo_ini velo_limit x_max y_max

0.01 0 0.025 50 24.5 0,0 0,0

0.01 10 0.025 50 24.5 32,3 3,1

0.01 20 0.025 50 24.5 48,2 10,3

0.01 30 0.025 50 24.5 54,7 19,4

0.01 40 0.025 50 24.5 54,4 29,0

0.01 50 0.025 50 24.5 49,0 38,1

0.01 60 0.025 50 24.5 39,9 45,9

0.01 70 0.025 50 24.5 28,1 51,9

0.01 80 0.025 50 24.5 14,5 55,6

0.01 90 0.025 50 24.5 0,0 56,9

Familia -rozamientos (Valores MKS)

kroz alfa_fle masa_fle velo_ini velo_limit x_max y_max

0 0 45 0.025 50 Inf 0,0 0,0 (cambiar ecuaciones

0.001 45 0.025 50 245 111,5 58,2

0.002 45 0.025 50 122 99,0 53,7

0.003 45 0.025 50 81 89,1 49,8

0.004 45 0.025 50 61 80,9 46,5

0.005 45 0.025 50 49 74,2 43,7

0.006 45 0.025 50 40 68,4 41,2

0.007 45 0.025 50 35 63,4 39,0

0.008 45 0.025 50 30 55,2 37,0 (error)

0.009 45 0.025 50 27 55,5 35,3

Vea ahora Rozamiento de aire a flecha II, para Rozamiento proporcional al cuadrado de la velocidad.