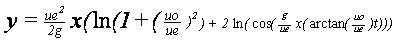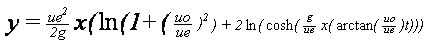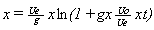Arco/Anteproyecto modelo de arco.htm

1c1. Pérdidas llamadas de histéresis, diferencia de energía

1c2. La pérdida de energía empleada en pandear (flexionar)

1c3. Y otras razones como

1c31 Incorrecta (no centrada) presión sobre la cuerda,

1c32 Rozamientos cuerda‑reposa‑botón, 1c33 Rigidez de cuerda, 1c34. Energía de desprendimiento de culatín‑cuerda. 1d. Velocidad de salida de la flecha 1e. Ángulo de salida de la flecha. 1f. Trayectoria de la flecha

1f1. Rozamiento proporcional a la velocidad.

1f2. Rozamiento proporcional al cuadrado de la velocidad. 1g. Componente transversal de la trayectoria. 1h. Influencia en trayectoria de la paradoja de la flecha

li. Otras influencias en la trayectoria: viento

1j. Influencia de inclinación y altura de diana. 2. MODELO ESTADÍSTICO 3. IMPLEMENTACIÓN INFORMÁTICA 4. DISEÑO y CONSTRUCCIÓN del ARQUERO MECÁNICO 5. BIBLIOGRAFÍA SUMARIA

RESUMEN El estudio propuesto consta de cuatro grandes temas, estrechamente relacionados: 1. El primero consiste en un modelo matemático determinista que considera el tándem arco‑flecha como una máquina mecánico‑cinemática que acumula energía y la cede a la flecha. obviando las influencia del arquero. Este modelo incluye principalmente:

1a. la acumulación de energía y su rendimiento en el arco al tensar.

1b. La reparto de esta energía entre el propio arco y la flecha, objeto del tiro, al soltar.

1c. Ángulo de salida de la flecha, según la geometría del arco y del arquero.

1d. la trayectoria de la flecha de acuerdo con las leyes cinemáticas, considerada como móvil pesado en un medio resistente.

1e. influencia en esa trayectoria de la flexión de la flecha y oscilación flectora subsiguiente de acuerdo con el par enderezador punta‑pluma.

2. El segundo se centra en un modelo estocástico del tiro se series de flechas, como Fita y Sala; quedan incluídos en él todas las incidencias del tiro, humanas y mecánicas, consideradas aquí como variables estadísticas. Consta de las partes:

a. función de distribución de los tiros a partir de variaciones en la posición relativa de arco‑flecha.

b. repercusión de esas variaciones en diana, de acuerdo con su tamaño y distancia al arquero.

c. función de distribución de puntuación, convolución de la función de tiro con la función diana.

d. correcciones de mira apropiadas a la estadística de los tiros realmente obtenidos, interpretadas según el modelo anterior.

3. La tercera parte del trabajo consiste en una implementación informática de ambos modelos, en tiempo real. Así sera posible "ver" todos los modelos anteriores. Se implementará en un ordenador PC compatible, con acelerador de coma flotante y pantalla de alta resolución; el lenguaje de programación será Basic, que reúne las virtudes de la sencillez, portabilidad, y rapidez de desarrollo. La rapidez de ejecución será conseguida compilando el programa una vez depurado.

4. La cuarta y última parte del trabajo se basa en el diseño y construcción de un Arquero Mecánico que simule el tiro humano con suficiente flexibilidad; el diseño puede variar entre un mero disparador hasta un mecanismo más sofisticado que permita simular características (y defectos) de los arqueros. Este dispositivo es completa y sirve de banco de trabajo de los modelos anteriores: en efecto, por un lado verifica o rechaza hipótesis incluidas en los modelos teóricos, y por otro muestra con regularidad mayor que el tirador humano el comportamiento del par arco‑flecha; en ambos casos el modelo teórico queda corregido y enriquecido.

UTILIDAD del ESTUDIO PROPUESTO La consideramos enorme y fundamental, por razones como las que siguen.

0. Mostrará la trayectoria real de la flecha, la cual sólo es conocida aproximadamente, incluso por arqueros expertos.

1. Contribuye ( o incluso inaugura, según nuestras noticias) con alguna profundidad el estudio técnico del tiro en su aspecto físico, en nuestro país, cubriendo un desfase grave con las potencias arqueras.

2. Dará al tirador un conocimiento de los aspectos físico‑técnicos del tiro, adquiriendo, creemos, seguridad y regularidad, es decir, puntos.

3. Ofrecerá una metodología de la corrección de la mira, de acuerdo con los tiros anteriores, lo que se hace hasta ahora, según nuestras noticias, de manera empírica.

Por supuesto, estamos completamente seguros de que el elemento fundamental del tiro con arco es el Arquero. Desgraciadamente, en él influyen tantos factores ( físicos, psicológicos, emocionales), y tan variables, que no pueden ser modelizados salvo en el aspecto citado en la segunda parte; quedan pues para disciplinas no científicas, al menos por ahora.

Pasemos a desarrollar con algún detalle los puntos propuestos.

1. MODELO MECÁNICO DETERMINISTA Considera el tándem arco‑flecha como una máquina mecánico‑cinemática que acumula energía y la cede a la flecha. obviando las influencia del arquero. Este modelo incluye principalmente: 1a. Rendimiento de la fuerza ejercida por el arquero. El rendimiento de la fuerza ejercida por el arquero para tensar el arco no es tan grande como pudiera pensarse, debido a que la proyección de la fuerza ejercida sobre ambas ramas de la cuerda no es normal al arco en la muñeca (punto donde la gaza engarza con las pala), siendo útil solamente la nueva proyección de esa fuerza sobre dicha normal:

fuerza flexadora = fuerza ejercida * sen ( cuerda‑pala)

como indica la figura. 1b. Acumulación de energía y su rendimiento en el arco al tensar. Los factores con más influencia en la potencia de un arco tensado son, como es sabido, la resistencia a la flexión de las palas, longitud de flecha y fistmele.(explicar)

│ .:

45 ┼ ..:

│ ...:

40 ┼ .....:

│ ..:.....:

35 ┼ ..::::.....:

│ ..:::::::.....:

30 ┼ .::::::::::.....:

│ .:::::::::::::.....:

25 ┼ .::::::::::::::::.....:

│ .:::::::::::::::::::.....:

20 ┼ .:::::::::::::::::::::.....:

│ .:::::::::::::::::::::::.....:

15 ┼ .:::::::::::::::::::::::::.....:

│ .:::::::::::::::::::::::::::.....:

10 ┼ .:::::::::::::::::::::::::::::.....:

│ .::::::::::::::::::::::::::::::.....:

5 ┼ .:::::::::::::::::::::::::::::::.....:

│ .::::::::::::::::::::::::::::::.....:

0 ┼ .:::::::::::::::::::::::::::::::.....:

┼────┬────┬────┬────┬────┬────┬────┬────┬───┬────┬── ─

5 10 15 20 25 26.75 30 pulgadas

fistmele

Representando la curva de tensión‑distancia encontramos un crecimiento de la fuerza ejercida en función de la distancia desde el reposa-flechas al encoque, hasta llegar a 26.75", distancia de la potencia nominal de los arcos en la actualidad. La fuerza nominal del arco será la que corresponde a esa distancia y debe ser aproximadamente igual a la marcada en al pala inferior del arco. La potencia total ejercida es entonces equivalente al área puntuada densa, que equivale a la integral de la fuerza ejercida durante cada incremento de camino recorrido. Si el arquero usa flecha de 30 pulgadas, por ejemplo, la potencia será mayor, incluyendo el área puntuada poco densa; esto corresponde al incremento aproximado de 2 lbs/pulg. Las palas del arco sirven como acumulador de energía. Pero no toda esta energía ejercida será recuperada al soltar, como vemos en el siguiente apartado. 1c. La reparto de la energía entre arco y flecha, A su vez, la energía almacenada en el arco tensado se empleará al soltar en mover tanto la flecha, como el conjunto palas‑cuerda. Suele expresarse esto atribuyendo a la flecha una masa virtual (mayor, claro, que la real) que dé cuenta de la menor energía útil para lanzar la flecha.

Ener.arco = ener.cin.flecha + ener.cin.palas‑cuerda =

= (1/2)* masa.flecha * (vel.fle)^2 +

+ (1/2)* masa. ar‑cu * (vel.ar‑cu)^2

= (1/2)* masa.virtual.fle.* (vel.fle)^2

c1. Pérdidas llamadas de histéresis, diferencia de energía recuperada al soltar y al tensar; son debidas a la rigidez o inelasticidad de las palas y pérdidas de calor

Estas razones justifican lel bajo rendimiento de la energía humana ejercida, rendimiento que puede variar entre un 40 y un 70 por ciento. Véase el gráfico 1c2. La pérdida de energía empleada en pandear (flexionar) la flecha. En efecto, la flexibilidad de la flecha, necesaria para un correcto paso por la ventana, precisa una cierta energía; siendo la flexión proporcional a la componente transversal de la fuerzas iguales y opuestas ejercidas sobre la flecha; ahora bien, estas fuerzas son las debidas a la inercia de la flecha, igual a su masa por la aceleración que adquiere.

F.in.fle = m.fle*ac.fle

Así, la flecha se ve sometida a una fuerza de pandeo proporcional a su propia aceleración, la cual disminuye desde un máximo al soltar a cero, al llegar a la "flecha" ( el llamado fistmele).

Esta fuerza decreciente de deformación flexiona la flecha hasta un cierto momento, en que la reacción elástica de la propia flecha, el momento resistente (ver((). La flecha abandona en algún momento ( a determinar ) la cuerda y comienza entonces a vibrar transversalmente, mediante una flexión contraria la inicial, salvando con ella la ventana, y realizando flexiones alternativas (paradoja de la flecha) que se atenúan progresivamente cuando se cumplen determinadas condiciones ( ver punto d. ). La frecuencia de vibración de flexión de la flecha es tanto mayor cuanto más flexible es (a demostrar en el proyecto). Es necesario entonces que ese período sea el exactamente necesario para salvar la ventana, sin lo cual la parte delantera de la flecha, si demasiado rígida) o la cola y plumas (si demasiado flexible) rozarán en la ventana, resultando un tiro desviado. 1c3. Y otras razones como 1c31 .incorrecta ( no centrada) presión sobre la cuerda, 1c32 .Rozamientos cuerda‑reposa‑botón, 1b33.Rigidez de cuerda, 1b34, energía de desprendimiento de culatín‑cuerda. 1d. Velocidad de salida de la flecha Aproximando la curva real presentada más arriba por una función triangulas, es decir, suponiendo crecimiento constante de la fuerza con la distancia, encontramos la expresión:

Energía = 1/2.mfle.vfle^2 = 1/2.Pnom.(d‑fis).(d‑fi)/(dnom‑fi)

con lo que la velocidad de la flecha, vfle, en función de la potencia nominal del arco, pnom, la distancia d de tiro real, la nominal, y el fistmele:

Para arco de 40 libras, flecha de 20 gramos, distancia de tiro de 28 pulgadas, siendo la dnom=26.25 pulgadas y el fismele de 10, encontramos una velocidad de salida de flecha de 241 km/hora, es decir, un valor muy verosímil. 1e. Angulo de salida de la flecha.

En el tiro se establece una geometría conjunta arco‑arquero, que depende de las geometrías fijas del arco (envergadura, longitud flecha), móviles del arco (altura mira, distancia soporte de mira a reposaflechas), fijas del arquero (altura ojo sobre flecha, grosor dedo flecha) y variables (atrasado de agarre respecto a barbilla e imponderables dependiendo de su calidad). Con todas estas variables, se produce en último extremo un triángulo que llamaremos Triángulo Fundamental, que es el que permite calcular eñl ángulo de la flecha con la horizontal. Véase la figura: Como se ve, la flecha tiene una longitud re.en, despreciando su exceso en el reposaflechas y suponiendo un agarre trasero del encoque, es decir más atrás de la proyección del ojo sobre la flecha ( caso de cuerda pasando al lado de la nariz, por ejemplo. Si la mira va montada sobre una regleta de longitud mi.re' a partir del reposaflechas, su altura sobre el reposaflechas es re.re', la altura desde el ojo a la flecha ( tomada perpendicularmente) es oj.oj', que viene dada por la distancia de ojo a mandíbula, más el grosor del dedo. Así tenemos la expresión del ángulo de flecha en la figura, en la que el numerador son alturas o distancias casi verticales y en el denominador distancias casi horizontales. Estos ángulos son em la practica pequeños, menores de 7 u 8 grados para 90 m y aún menores para las otras distancias. Conocidos la energía que recibe la flecha y su ángulo, resulta posible calcular su trayectoria. 1f. Trayectoria de la flecha Consideremos la flecha como un móvil pesado en un medio con rozamiento. Sea este rozamiento exclusivamente el Longitudinal o frontal al avance, es decir, que se mueve siempre tangente a la trayectoria. Y encontremos las trayectorias para rozamientos proporcionales a la velocidad y al cuadrado de ella. 1f1. Rozamiento proporcional a la velocidad. Proyectando las aceleraciones sobre los ejes:

m.y" = ‑ m.g ‑ k.y'

m.x" = ‑ k.x'

Integrando de manera inmediata estas dos ecuaciones diferenciales se obtienen fácilmente las ecuaciones paramétricas de la trayectoria:

Ue.u0 + ve ‑(gt/Ue)

y = ‑‑‑‑‑‑‑‑‑‑–––– . ( 1 ‑ e ) ‑ Ue.t

Ue.w0 ‑(gt/Ue)

x = -‑‑‑‑‑- . ( 1 ‑ e )

de las que se obtienen las coordenadas del punto x, y en el instante t, de una flecha que sale con velocidad v0 y un ángulo al con la horizontal; u0 y w0 son las proyecciones de esa velocidad sobre ejes vertical y horizontal, o sea: u0 = v0.sen(al) w0 = v0.cos(al) Ue es un parámetro dependiente de la masa de la flecha y del coeficiente k de rozamiento, de expresión: Ue = m.g / k que resulta ser la llamada velocidad límite, que alcanzaría la flecha dejándola caer verticalmente; g es la aceleración de la gravedad. Véanse en la figura adjunta las trayectorias cambiando la influencia del rozamiento; nótense sus formas y alcances diferentes. f2. Rozamiento proporcional al cuadrado de la velocidad. Proyectando las aceleraciones sobre los ejes, al subir, y al bajar:

( m.x" = ‑ k. x' ( m.x" = ‑ k. x'

     Integrando de manera inmediata, se obtiene, al subir:

              y al bajar:

es decir, idéntica, excepto el cambio de coseno al subir por coseno hiperbólico al bajar.      La abscisa es común para ambos tramos:

           la velocidad límite Ue vale aquí:                               ___________                   Ue = √ m.g / k siendo iguales el resto de los parámetros. Véanse en la figura    la trayectorias cambiando la influencia del rozamiento; notese sus formas y alcances diferentes.    Nos proponemos una mayor exactitud, aproximando el rozamiento mediante una expresión proporcional a           roz = k . ( a + b.v + c.v^2 )      Paralelamente mediremos la velocidad real de las flechas mediante aros magnéticos y un computador que medirá tiempos y distancias. 1g. Componente transversal de la trayectoria.     Viene relacionada con la desviación inicial de la flecha, es decir, adonde apunta, respecto al plano vertical que contiene arco y flecha; esta desviación depende de cuánto hemos sacado el botón de presión (Berger), o en su defecto, donde sitúa el reposaflechas a la flecha, respecto a ese plano.

     Esta colocación depende de la situación de la mira y el ojo respecto a ese plano. La dependencia de todos estos factores viene reflejada en los gráficos siguientes.

                            flecha

   @══>>>>>════════════════════════════════════╤═╤═════════@

                                               │ │                 mira

       ( ‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑│ │‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑▌▌▌

      ojo                                      │ │                   │

                                               ──┴─┴───────────────────┴──

                                               botón

        ojo                                                          mira

         ( ‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑▌▌▌

                                                                       │     @══>>>>>════════════════════════════════════╤═╤══════════@        │                            flecha              │ │                   │                                                │ │                   │

──┴─┴───────────────────┴──

                                               botón

  Se observa que mira y botón se conforman de manera opuesta según el ojo sobre la flecha. A su vez, la posición de ambos elementos, notifica al arquero de esa situación (quizá a corregir). El problema queda complicado por la flexión de la flecha, necesaria por un lado, como dijimos, para salvar la ventana del arco, pero que luego ocasiona un culebreo con capacidad de desviar la flecha, según la flexibilidad.     1h. Influencia en trayectoria de la paradoja de la flecha Una vez en vuelo, la flecha, dotada de en una cierta flexión, se mueve culebreando, movimiento que podemos descomponer en otros dos: uno absoluto, de acuerdo con la trayectoria del centro d4e gravedad obtenida en c, y 2) la velocidad relativa de la flecha respecto a ese centro, curvatura y cabeceo. Para estudiar esos movimientos relativos, observaremos el móvil sometido a su velocidad constante tangente a la trayectoria y situada en el c.d.g ( adelante, 7,9,11 %) la velocidad de signo mas bien contrario ocasionada por los rozamientos ( frontal y transversal) de la flecha, localizados sobre todo en las plumas (atrás).

La oscilación flectora produce un sistema de fuerzas que hacen culebrear la flecha en sentido horizontal, culebreo que puede alcanzar decenas de centímetros con la consiguiente desviación en diana y en puntos. La visión y medida sobre un vídeo a cámara lenta de la salida de la flecha, nos ha permitido observar que ésta oscila alrededor de 25 veces por segundo, lo que equivale a una oscilación (doble) cada 2 o 3 metros. Entre 30 y cincuenta metros la flecha oscila unas 8 veces. Se trataría pues de adecuar exquisitamente la flexión para que se produzca un número exacto de veces cada 20 metros ( en Fita) y cada 7 en Sala. Esto nos da idea de la complicación del ajuste del arco. Es nuestro propósito realizar vídeos sobre esta materia para conocer en detalle las flexiones de la flecha. N1i. Otras influencias en la trayectoria: viento No estudiado hasta la fecha, pero dentro del proyecto. 1j. Influencia de inclinación y altura de la diana. Aunque el tiro con arco es habitualmente horizontal, no conviene olvidar los casos en que arco y diana están a diferente altura, como tiro de campo y modalidades poco usuales. Esto tiene su repercusión en la trayectoria, evidentemente. Incluso en los tiros habituales como Fita y Sala, hay un desnivel entre ellos, que tiene su importancia; por ejemplo el amarillo de la diana está a 1.30 metros mientras que un arquero alto mantiene su arco por encima de 1.60. A 18 metros esto representa un ángulo de artan(.3/180), o sea casi 1 grado. A su vez, la inclinación de la diana, 15 grados, influye en cuanto la apertura que ofrece al tiro según la distancia y potencia. Como los ángulos de llegada son pequeños, de 1 a 12 grados aproximadamente, resultan algo favorecidas las grandes distancias.

2. MODELO ESTADÍSTICO      El modelo anterior nos permite conocer la trayectoria de una flecha. Pero )como conocer el comportamiento de una nube de flechas lanzadas por un arquero durante una competición, Fita, por ejemplo?. Para ello necesitamos caracterizar el carácter variable, impredecible para cada flecha, pero predecible en su conjunto, de acuerdo con la calidad de arquero. Ello nos viene dado por una variable Aleatoria, de distribución desconocida, pero que supondremos normal o gaussiana. Es decir, supuesta correcta la posición de la mira, consideramos que esa posición sufre un error variable en cada tirada, y ello para cada característica del tiro que influye en él, como posición horizontal y vertcal de la mano del arco, longitud real de flecha, paradoja, viento, etc. Tendremos caracterizado pues el tiro de una nube de flechas por una Función Tiro, dependiente por un lado del Par Arco‑Flecha y por otro del Arquero. La nube resultante de la función Tiro, llegará a la diana como un haz, cuya apertura y forma dependen de la distancia a la diana, y aunque poco de su inclinación (15 grados). Llamamos a esta Función Repercusión. La nube en diana resulta ser otra variable aleatoria, dependiente de la anterior según la Función Repercusión.

puntos│

      │

   10 ┼                             ┌─────┐

      │                          ┌──┘     └──┐

    8 ┼                       ┌──┘           └──┐

      │                    ┌──┘                 └──┐

    6 ┼                 ┌──┘                       └──┐

      │              ┌──┘                             └──┐

    4 ┼           ┌──┘                                   └──┐

      │       ┌──┘                                         └──┐

    2 ┼     ┌──┘                                               └──┐

      │ ┌──┘                                                     └──┐

    0 ┼──┼──┬──┼──┬──┼──┬──┼──┬──┼──┬──┬──┬──┼──┬──┼──┬──┼──┬──┼──┬──┼─

         │blanc│negro│ azul│ rojo│ amarillo │ rojo│ azul│ negr│blanc│ color

‑40   ‑32   ‑16    ‑8     0    ‑8     0     8    16    24   cm

Función Puntuación FITA, 90‑70 m.

Una vez en diana, entra en juego su tamaño y puntuación atribuida a sus diversas zonas, todo lo cual depende de la modalidad de tiro (Fita, Sala, etc.). Veamos representada la función puntuación correspondiente a Fita 30‑50 m, diana de 80 cm. de diámetro. La nube alcanzará una cierta puntuación de acuerdo con su centrado, apertura y distribución. Los puntos obtenidos serán caracterizados por una nueva función, llamada Función Puntos. Resulta claro demostrar que Puntos es la convolución ( Ë ) de Repercusión del Tiro con Puntuación:                     Puntos = Rep ( Tiro) Ë Puntuación                Maximizar ese función puntos es el objetivo general del Tiro con Arco (dejando fuera la caza y la guerra, naturalmente).

             frecuencias      .

puntos│                      .:.

      │                      :::

   10 ┼                     .:::.   ┌─────┐

      │                     :::::┌──┘     └──┐

    8 ┼                    :::┌::┘           └──┐

      │                   .┌::┘:::.             └──┐

    6 ┼                 ┌─:┘:::::::                └──┐

      │              ┌──┘:::::::::::                  └──┐

    4 ┼           ┌──┘ .:::::::::::::.                   └──┐

      │        ┌──┘ .:::::::::::::::::.                    └──┐

    2 ┼     ┌──┘ .:::::::::::::::::::::: .                    └──┐

      │ ┌──┘ .::::::::::::::::::::::::::::::.                    └──┐

    0 ┼──┼─.┬──┼──┬──┼──┬──┼──┬──┼──┬──┬──┬──┼──.──┼──┬──┼──┬──┼──┬──┼─

         │blanc│negro│ azul│ rojo│ amarillo │ rojo│ azul│ negr│blanc│ color

‑40   ‑32   ‑16    ‑8     0    ‑8     0     8    16    24   cm

Funciones Rep(Tiro) y Puntuación.

Por ejemplo, en el gráfico tenemos representado una distribución de tiro normal o gaussiana, correspondiente a un mal centrado de la mira (bajo), que dará lugar a una media de unos 7.5 puntos por tirada. La convolución consistirá en multiplicar la puntuación de cada zona por el porcentaje de flechas que se espera en cada una, o sea:

3.2% + 4.3% + 5.6% + 6.10% + 7.30% + 8.30% + 9.10% + 10.6% +10.3% + 9.2% = 7.5 aprox.

Naturalmente, los puntos crecerán aumentando el tamaño de diana y disminuyendo la anchura del haz ( siempre que éste esté centrado), acortando la distancia. La función tiro representa la calidad del tirador, y esta calidad se traduce en puntos según distancias, dianas y puntuación. Esto nos permite comparar dos tiradores en distancias o modalidad diferente, o bien suponer cual será el comportamiento de un tirador en una modalidad, conocida su puntuación en otra. Estimemos de los parámetros de la función Tiro, a partir de observación de tiro real.

Aún suponiendo que la distribución de tiro es gaussiana, hay que estimar los parámetros de esa distribución, que son dos, como es bien sabido, la media y la desviación típica. Empleando dos estimadores conocidos, encontraremos que la estimación de la media, es la media de los tiros; y la desviación típica esperada viene dada por la expresión: 3. IMPLEMENTACIÓN INFORMÁTICA Los dos modelos anteriores, el matemático ‑ mecánico - cinemático - determinista y el estadístico ‑ aleatorio pueden ser simulados en el ordenador. De esta manera se 've' cada flecha volar de acuerdo a sus parámetros de tiro y fallar o acertar la diana, contabilizándose los puntos obtenidos. Si los parámetros se toman fijos, se obtiene un tiro idéntico. Si variables aleatoriamente, se tiene una aproximación al tiro real de series. Pueden ser así 'comprobados experimentalmente' las hipótesis que se hagan. La representación gráfica es una ayuda intuitiva eficaz en la comprensión de lo que ocurre, de ahí su aplicación educativa. Se implementará en un ordenador PC compatible, con acelerador de coma flotante y pantalla de alta resolución; el lenguaje de programación será Basic, que reúne las virtudes de la sencillez, portabilidad, y rapidez de desarrollo. La rapidez de ejecución será conseguida compilando el programa una vez depurado. 4. DISEÑO y CONSTRUCCIÓN del ARQUERO MECÁNICO La cuarta y última parte del trabajo se basa en el diseño y construcción de un Arquero Mecánico que simule el tiro humano con suficiente flexibilidad; El diseño puede variar entre un mero disparador hasta un mecanismo más sofisticado que permita simular característica ( y defectos) de los arqueros. Este dispositivo es completa y sirve de banco de trabajo de los modelos anteriores: en efecto, por un lado verifica o rechaza hipótesis incluidas en los modelos teóricos, y por otro muestra con regularidad mayor que el tirador humano el comportamiento del par arco‑flecha; en ambos casos el modelo teórico queda corregido y enriquecido.
5. BIBLIOGRAFÍA SUMARIA Frederic, Louis. Tir a l'Arc. Laffont Paris, 1985 Paterson, W.F. Encyclopedia of Archery. Hale, London,1984 Puig Adam, P. Cálculo Integral, ETSII, Madrid,1962 Puig Adam, P. Ecuaciones Diferenciales. ETSII   Madrid,1950 Lucini,M. Teoría de la Mecánica. Labor, Madrid,1950 Cadet, J. Technologie du Tir a l'Arc Competition. Cadet, Paris,1977? Ríos, S. Métodos Estadísticos. Autor, Madrid,1968 Baier,Bowers. Instructor's Manual. N.Ar.As USA Easton, Beman, Yamaha. etc. Catálogos Técnicos. Vídeo de la Federación de Arco de Canadá.

Vuelta al Principio    Última actualización: lunes, 07 de mayo de 2018    Visitantes: