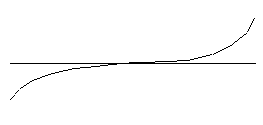frecuencia y tono

Aunque familiarmente –en las familias dedicadas a estos temas, claro– se suele decir que el tono de una nota es su frecuencia, esto naturalmente no es verdad. Lo que hay es que cuando un objeto vibra con regularidad es decir un número de oscilaciones por segundo (esto es la frecuencia ) constante, el oído percibe lo que llamamos tono. Así que la frecuencia es lo que pasa y el tono lo que sentimos y percibimos .

También ocurre que cuando dos frecuencias son una doble de la otra, el oído percibe entre ellas una relación agradable de coincidencia o fusión que llamamos consonancia . También percibimos una sensación de diferencia entre ambos tonos que llamamos intervalo, y en este caso de frecuencias una el doble de la otra, frecuencias en proporción 2:1, el intervalo es llamado octava (¿Por qué octava`? -por que las músicas del mundo suelen poner seis tonos intermedios entre ellos dos, con lo que tenemos ocho). También sabemos que cuando la proporción de frecuencias es 3:2 (estos dos números separados por dos puntos, significan en acústica que hay dos sonido con frecuencias en esa proporción que suenan simultáneamente, de modo que no es un intervalo ascendente y descendente, sino una proporción de dos frecuencias concurrentes) ¿Y como se median antes las frecuencias de dos sonidos? tras comprobar que la frecuencia que emite una cuerda vibrante depende de su longitud, es inversamente proporcional a ella, bastaba con pulsar dos cuerdas en una determinada proporción de longitudes para que las frecuencias presentaran una proporción inversa. La cuenda mas larga emitía la frecuencia mas larga. En realidad no se medía la frecuencia sino que se oía el tono que era para la proporción 2:1 un intervalo de octava. (queda pendiente el enterarse de cuando se empezó a hablar de vibraciones y no de longitudes de cuerda).

Pero dejémonos de disquisiciones aunque sean pertinentes y volvamos al punto del título.

Si medimos con precisión las frecuencias de los sonidos que forman las proporciones simples que el oído consagra como consonancias, las únicas que permiten afinar al oído un sonido con otro ( seria imposible afinar al oído un sonido con otro que tenga 2,31 veces su frecuencia), observaremos que la sensación de octava se obtiene no con una razón de frecuencias 2:1 exacta sino que el oído educado musicalmente se siente satisfecho cuando esa proporción es ligeramente mayor es decir que la octava musical proviene de una proporción algo mayor que el doble in frecuencia, este hecho pasaba desapercibido antiguamente porque no se median frecuencias o se median sin precisión .

Y esta medida ampliada de la octava, se produce mas en las frecuencias extremas que en las medias .

Es decir es el oído educado el que debe decidir las frecuencias adecuadas para las notas oyendo y no midiendo.

Una alternativa subóptima es saber el valor de esa octava ancha y aplicarlo a la afinación.

Esta modificación secuencial se aplica empíricamente en la afinación de un piano. Pero no la hay en la fabricación de teclados electrónicos, que sepamos, lo cual lo convierte en instrumentos insatisfactorios por esta razón debida a la afinación y por otras causas.

Comparación entre una afinación convencionalmente matemática (octavas de 2:1) , y la función de énfasís frecuencial, cuya ecuación puede aproximarse con: una función del tipo de ARCO TANGENTE

Estas octavas anchas ocasionan que los agudos sean mas agudos que los matemáticamente previsibles y que los graves sean mas graves que los matemáticamente previsibles . De modo que se trata de aplicar una función de variación de la frecuencia que levante esos agudos y baje esos graves. Es una función casi horizontal en el la 3 ( 440) hz y se curva a derecha agudos hacia arriba y hacia abajo en graves a la izquierda.

La variación e n los extremos puede llegar a unos 20 a 30 cents, es decir como 1/4 de semitono .

Hagamos una experiencia: En nuestro teclado modal cuyas teclas son afinarles una a una, elijamos dos sonidos en proporción perceptiva de 4 octavas y midamos después sus frecuencias.

El resultado ha sido que dos oyentes con formación musical han encontrado satisfactorio un intervalo de 3 octavas en la que el agudo estaba 40 cents mas alto que la afinación matemáticamente convencional. Es decir ¡casi medio semitono de error aparente! o bien mas de un 5% de error sobre aquella afinación .

Otro oyente con formación gustó de un incremento de 45 cents entre dos SOL a tres octavas. casi igual. Parece que es un requerimiento general del oído. En los extremos más: por ejemplo con timbre de armonio, grave, el mismo oyente, aunque no se percibe bien el tono, se quedó con 50 cents de énfasís en 2 octavas

Prácticamente, en una guitarra, por ejemplo, las cuerdas graves deben afinarse al aire un poco más bajas, las agudas más altas y los trastes deben ser un poquitín más grandes, respecto no ya al regla del 18, sino también a la regla temperada, por esta razón.

El autor compuso música con medios muy primitivos hacia 1983 aplicando esta variación: se describe en parte aquí: computing for humanities.