 |
Esta página está en construcción: perdonen los errores, repeticiones y temas inacabados.
This page is being developed: I am sorry for errors, duplications and unfinished subjects.
COMPUTING for HUMANITIES
KEYWORDS:
Humanism, Perception, Aesthetics, Art, Music, Poetry, Performance, Sport, Programming.
ABSTRACT.
From the past to the modern times, a human attitude, a type of Man has pervaded History: critical, polished, cultivated, competent in Letters, Techniques and Arts, the Humanist. His tool is now the computer, a computer capable of offering degrees of subtlety compatible with his. It must be his prolongation, his arm, as such it should incorporate many of his qualities and features. In this paper the author shows some of his software applications which illustrate, he believes, this humanistic flavor. They are related with Nature, Sports, Perception, Art, Poetry, Music and Beauty.
HUMANITIES
While we are not certain about what exactly Humanism and Humanities mean, according to the cultured use of these terms including the terminology used in the present congress , they may be synonyms, cover, or suggest subjects as Thinking, Culture, History, Philosophy, Literature, Letters, Arts.
In modern times, Humanities have been opposed to Science and Technology in the academic and research world, by dividing activities, curricula, institutes. They have, in common language and taste, a feeling of subtlety and human understanding, in contrast with a dryer and more exact approach to things, assigned the last two disciplines. We will see that this is no longer (if it was ever) the case.
Humanism, as a social and cultural movement or civilization from the fourteenth to the sixteenth century, seems to be an affirmation of human values, rights and qualities, as opposed to an extremely oppressive mediaeval concept of Man by the Church(es), drawing its strength and contents from the classical antiquity ( mainly Greece but also Rome ). The printing press made communication and diffusion of Culture, easy. Universities were born and Trivium and Quadrivium studies formed, by including scientific and letter disciplines, widely cultured men. A new critical mind, a more daring attitude, a growing confidence in the human mind and possibilities, gave way to new travels and discoveries, a new joie de vivre.
The Renaissance, in the Italian republics and other countries, feeding extensively on this past, fertilized Architecture, Poetry and Literature, Music, Science and Crafts; almost every kind of human activity was turned upside down and improved. The Oriental world, through these antique channels, and also directly, merged in this rich blend as well, the fruits of which still continue to marvel us.
In brief, a new man was born (or reborn), a man with polished manners, with a feeling for language, especially Latin, eloquence, educated in arts, letters and techniques, in the art of war, in commerce: a sort of perfect man, an 'insân al-kamîl (
_°§«[ ²\wÉ ), except by his moeurs.PROTAGORAS
Few fragments remain of the leader of the sophists, of which the following is the most popular:
Man is the measure of all things, of thing that are that they are, and of thing that are not that they are not.
Many meanings can be found in this short sentence; among them, that of the relativity of everything, including ethics and religion, a reason for which its author was criticized and rejected by Plato, Aristotle, the whole Athenian society, and even ours. However, it is well known that dialectics, professional education, equalitarian society (all respectable modern activities, qualities or ideas) can also be linked to sophist thought.
But here we prefer to concentrate on one of its possible senses, pretended or not by Protagoras (we think though that it was the case), but convenient anyway: Man, as vehicle of everything said and therefore thought , perceives, judges, measures, according to his qualities and properties. A vibration of air is sound if its frequency falls inside the range of the hearing sense; an electromagnetic wave is color if its frequency is perceived by the eye. Concepts as big, small, high... are applied to objects according to the human size, senses and experience. Even Moral and Ethics are relative to human rule: between human and animal life, always the human will be preferred, by humans. And so on.
COMPUTING
Speaking of the last decades, when computers emerged, computing was initially an extremely tiresome duty: data were provided to memory and registers in binary or byte format, as programming was machine-oriented. Programming languages followed, allowing humans an easier data management, approaching human language, i.e. the human conception of things ( go to, stop, continue...). Gradually programs became more human oriented, incorporating other information means than letters and numbers: colors, drawings, graphics, sounds, were introduced in a more user-friendly approach, until the present ( but also episodic ) day, when multimedia, hypertext, information highways, have become common language and experience of modern children. Therefore, modern computing has become more and more human, at least in the sense of proximity and easiness of its programming. But what about now and the future?
INCORPORATING HUMAN PERCEPTIONS in COMPUTING
A first adaptation of programs to the human perceptions was the already mentioned inclusion of sensible means as communicating tools: graphics and colors and sounds as speech and music. But not only this material should bring computation and products of computing nearer to human sensibility: their ranges of variation and the scales in which these ranges are presented must be also human-like. This means that, for instance, if images are represented by means of grey shades, the greyeness must be ordered in human steps. If sound is provided into a program, its pitch and intensity should be independently accessible, and this, in steps according to human perception logarithmic-like steps as reflected in Fechner's Law, or even another more sophisticated model of sound perception . Music applies these models when it uses notes, that is, pitches ordered in geometric-ratio steps.
What does all this mean ? This shows, in fact, a growing inclusion of human models of perception in computer programs. Not only perceptible stimuli are used, but they must be ordered within human perception and structure. And this structure can be natural or social: in any case the stimuli become human, rather that mechanical.
ARTIFICIAL INTELLIGENCE
Cybernetics, initially born as an injection of human neurological feed-back in electronics, taught computers to react to local conditions, a very characteristic feature of life. This was the beginning of learning. With the addition of sensors to the computer, it began to feed directly on the environment, rather that through the keyboard. It could measure now, thus becoming a specialized tool, which simulated hundreds of others: it could measure weights, lengths, illuminations, noise levels, electrical field, sizes, and so on.
The next step was to do something with these measures, what humans do: extract some conclusions, establish logical decisions, naming things, recognizing things. Pattern recognition was one of the first and useful intelligent tasks accomplished by computers. Others followed, entering in the modeling of intelligence itself (cognitive psychology) and using the human terminology (intelligence, neural nets). Speech recognition, in the phonetic, lexical, syntactic and semantical levels, incorporated more and more language models, i.e. Reality models.
AESTHETICS
Going into more subtle properties of human perceptions, we arrive at Aesthetics, another ill-defined concept related to Humanities. There are doubts, here as well, about the methods and contents of Beauty: we are still confused as how to prove that a given oeuvre d'art is better than another, or even that it is good, out of the inner conviction that it wakes in cultured minds, a weak claim for objective truth. However, some features have been found in common in these reputedly good masterpieces: Unity in the Variety, and the other way round, are almost always present. Another fundamental feature is also observed in the most abstract arts, Music and Architecture: Number, integer numbers in the proportions between the values of the perceived quantities in those Arts. Visual proportions and musical intervals are excellent examples of that.
PERSONAL EXAMPLES
The author has been programming humanities for 20 years, avant-la-lettre, so to say in that way. Some examples of this approach are here presented, showing, in greater o lesser quantity, the approach commented before: the introduction of human qualities into the program itself, to adapt it to human understanding and aesthetic perceptions. Some of these programs are more sophisticated than others, but all show, we think, this humanist flavor, either in its use, in its performance or in its (audible, visible) results.
The themes of these applications belong to the visual kind: Tree Growing, Archery, Islamic Tessellations; and the audible one: Psychoacoustic Tests, Automatic Music Composition, Measurement of Oriental scales and Persian Poetry. Let us review briefly all these areas.
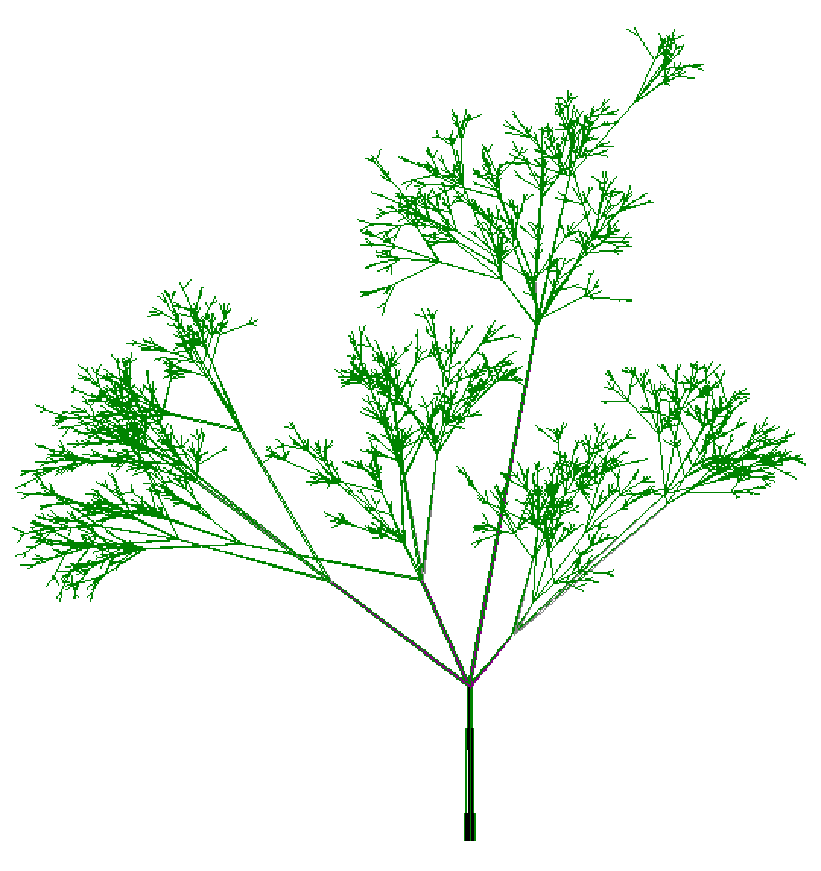
NUMBER, ORDER and DISORDER in NATURAL TREES
*Natural trees are shown here as visual exponents of abstract concepts of numbers, order and disorder. The influence of several parameters of growing, as number of branches, angle of openness, reduction factors of branch length and width are seen as a global appearance immediately perceived as a type (species). Furthermore the variation of these few parameters gives huge differences in the whole tree, showing the power of repetitive and systematic little trends in nature.
In the observation of actual trees present in nature, it is easy to note the constancy of physical characteristics for each species. The number of branches in each node, the ratio of branch length reduction are almost-constant for a particular variety. On the other hand, these trends, however modified and influenced by random natural circumstances, cause the tree to have a general aspect which is immediately related to that particular species.
 |
This, for us, reveals a relation between the number and nature. But in nature we can see a freedom with these rules, a 'natural attitude' (let us remember the use of this word in the context of human behavior or in fashion) which also characterizes nature in general and trees in particular.
We see that a balanced combination of order and disorder are necessary ingredients in natural beings. Ingredients which can be roughly attributed to heritage (order) and ambiance (disorder). Life can be considered as a plan with circumstances which modifies this plan until a certain point.
The degree of that variation presents two extremes, both non compatible with life: if there is no variation in the plan, if everything is order, the tree presents a kind of cold perfection, akin to artificial objects. If, on the contrary, everything is disorder, random changes, the product is a pathological being, no able of sustaining life. See the figures (???) to show these extreme situations.
These trees have been repeatedly used by the author to illustrate the limits between which Art, and Music, should move, partially satisfying expectations, partially frustrating them, i.e. surprising.
The program was written in 1978, well before the present fractal fashion.
ARCHERY
So the trajectory of the arrow is represented in real time, after evaluating the computer speed on which the program is run. For each point of this path, arrow height, distance to archer, direction, velocity and acceleration can be recovered and printed. The trajectory, drawn in this way, varies between the theoretic parabolic one when there is no friction and the popular empiric one, which believes arrows to fall vertically at the end of a high fly.
The impacts on the target ( if any !) are represented as well. Scores are computed shot by shot, according to the weight attributed to each circular frame/color (five colors, ten circles valued from 1 to 10). If no target is used, or if situated out of the arrow paths, there is no score and the reach of the system bow-arrow is obtained.
The session or round is characterized by a determined number of arrows at a determined number of target distances. The outdoors international are those adopted by the FITA: 144 total shots, 32 arrows for each of four distances (men: 30, 50, 70 and 90 meters; women: 30, 50, 60 and 70); the first two distances using a target external diameter of 80 cm and the other two, one of 122 cm. Indoors the distances and diameters are: 18 (diameter: 40 cm). and 25 meters (60 cm), 30 arrows per distance. In USA some other rounds are also used.
After the whole set is shot there is the possibility of correcting the reference direction of the bow, using the information that the impact cloud suggests to the (simulated) archer. Eventually, the program itself is able of this correction, in horizontal and vertical orientations, improving the performance as much as its random (human or mechanical) movements allow. The program show thus how to center the bow during an actual shooting, from the not always obvious information that the cloud provides.
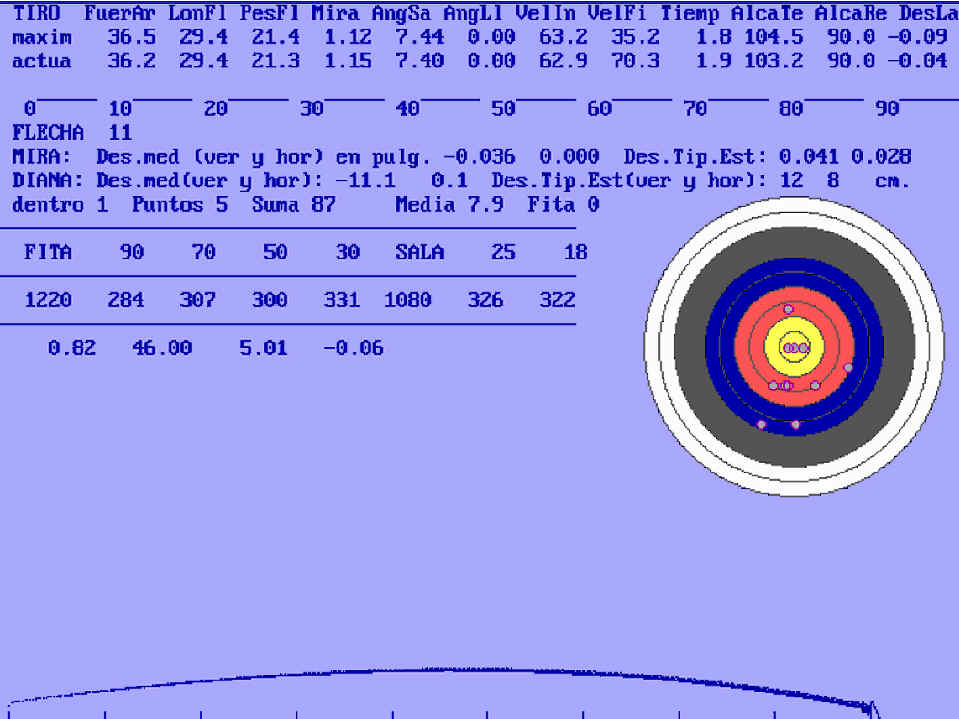 |
A simulation of archery has been developed, where many features and parameters, including the human, cooperate to show the behavior of a whole session of shooting. The main factors are the bow, the arrow, the air, the target and the archer, each one with its own parameter set.
The bow is defined by its weight (drawing force when extended), fistmele (distance of arch center to the string), the string weight and the bow spacial position, defined by its horizontal and vertical angles. The opening scope of the bow will be governed by the arrow length. The sight situation is also a parameter of the shooting ( the sight is a little circle on a perch attached on the bow side, that protrudes from it and on which the sight can be displaced in horizontal and vertical directions.
The final direction of the shot depends on the relative eye and bow sight positions, which will fix both hands position, left on the bow center and right drawing the string back, with the feathered arrow extreme between the fingers. All this determines two angles with the horizontal and vertical references.
The arrow is defined by its length, its weight and a friction factor depending on the transversal area that counters the air when flying.
The air medium is characterized by its friction factor and the dependence of this factor on the arrow velocity - a 2nd. degree polynomial expression.
The target is the usual one, composed by several concentric circles, on a plane surface, whether vertical or slightly tilted. It is defined by its size (diameter), position and situation (distance, height) with respect to the archer.
The archer is simulated by some movement of the arrow direction, defined by two random horizontal and vertical variables with a Gaussian distribution law. These direction increments are multiplied in their effect by the distance to the target, producing a volley of impacts around the reference point, which can be centered or not on the target center ( the yellow, from the inner circle color ).
The flight of the arrow is simulated point by point, calculating changing arrow direction, velocity and position in it, by an integration of the corresponding differential equations. These equations are different for rising and falling directions due to the coincidence or opposition between the gravity and acceleration directions in both situations. The equations equally change depending on the exponent of velocity in the friction force expression.
TESSELLATIONS in ISLAMIC PATTERNS
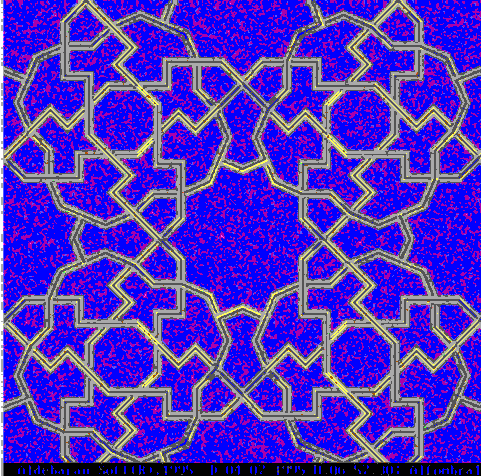
Archeological and artistic analysis of Islamic patterns needs the prior understanding of their geometrical design and properties: otherwise only fake patterns are obtained, and thus beautiful decorative designs are lost to the comprehension of scholars and admirers. Any pattern can be analyzed and drawn by means of the graphical design package PU18. The original pattern in the photographic images must be first improved and its minimal shape found, i.e., the shape that reconstructs the whole figure by translations, gyrations and symmetries. A basic step is to find the net order over which the lacework is woven, that is, the number of different directions in the plane appearing in the figure. The form is thus reconstructed for further repairing or reproduction.
To reach a acceptable enough model of an actual graphic -called, from now on, the original-, two approaches are necessary: the principal one is to understand the geometric regular properties of the lattice over which the design ( here called Rige ) is built, from choosing some of the segments that appear in the lattice. The second one, of a secondary nature, is to superpose both figures to visually assess their similarity. The necessity of the first method is absolute: it is virtually impossible to make two figures exactly coincide when one or both of them are the reproduction of a natural object; these figures are never perfectly regular; moreover, the process of obtaining the image (photograph, print, photocopy, video, scan) introduces its own deformation, some of then natural, like perspective angles and light; some of them belonging to the technique used: resolution or grain, film or tape quality, noise, etc.
Therefore a theoretical model is essential to overcome these difficulties. On the other hand, the mental and visual comprehension of a figure is always required: the observer makes some rearranging, some hierarchical ordering and selection, without which no visual perception is possible. In our case a regular geometric model is necessary, both to understand the image and to draw it.
The model realization of an original Rige is based on several assumptions, which narrow the infinite possibilities of parameters values. These basic assumptions conform a General Model of Rige figures, that allow us to interpret them by means of it, simplifying the choices: an angle will be one of the multiples of 2.PI/N, but not an intermediate value; a distance will be a particular linear combination of the basic distances, but only with integer coefficients.

Such a model of Islamic rectilinear patterns derived from the observation of many figures of this kind has been presented in [Sánchez,93;95;96]. It consists of a set of rules that every actual pattern seems to comply with. The model is embedded in a computer package that provides these rules for the designer, allowing the economic coding of each pattern. Several figures edited and drawn with this package were also presented, in order to assess visually the validity of this model.
An important value of this general Rige model is that of the preservation of its shape throughout time: without it, the copying of a Rige by means of the secondary approach, trial and error, will bring a gradual degradation of this shape, loosing its beauty and sense, becoming a fake without internal coherence, and disappearing, like a degenerated species, through imitation and restoration. Some of these unfortunate cases can be seen in reproductions past their historic moment. These "modern" fakes are however sometimes as old as the seventeenth century.
In Information Theory, Redundancy is used as a way to built robust messages, that is, messages that go through the transmission line and can be recovered afterwards, even in the presence of noise. The redundance consists on repeating some information (codes) in the message; in this way, an eventual degradation of one of its repetition would not imply the loss of it, since the same information can be recovered from another one.
In the same way, a Rige must have redundance to make its shape robust against noise, this being, in our case, the physical and human transformation that the form suffers through the time (centuries or millenia). If there is a meaning in the Rige (and we are sure this is the case indeed), this meaning will be protected by a robust (redundant) shape. Redundance consists, in our case, of symmetries, similitudes and equalities, coincident points and straights. This lead us to an economy of constructible elements, or better said, to parsimony, the old (but eternal) concept closely related to style, elegance, beauty. We thus arrive at one of the ways that Tradition conveys messages, meanings to posterity: designs with an in-built protection, that is, nondegradable forms. These considerations give us a new rule:
Lattices and forms will be as simple and economical as possible, reducing the number of different elements ( i.e. not reducible to others by geometrical transformations) to a minimum.
Illusion and Deceit. - Another characteristic of Rige Art is forcing slightly, up to certain point, the exact proportions and angles to deceive the observer into making visual interpretations belonging to another geometric world: we refer to metabolê, the visual correlated element of musical modulation, as we saw in [Sánchez, 93].
But we especially refer to the enharmonic metabolê, by which we understand the kind that is not evident, the metabolê that fakes another one. In this case the eye, like the musical ear, attributes a double belonging to a segment, which can be understood as fitting it into regular patterns, which belong in turn, to two ( or more ) lattices with close but slightly different angles or distances. This adds another rule, somewhat opposed to the former one:
A segment can be slightly slanted, bent or displaced to comply with several lattices.

Symbolism
. The Islamic craftsman gives a deeper meaning to his designs by means of a symbolic message, usually religious and numerical. In this way, his work and its product acquire greater importance. This meaning must also be understood by the observer, in order to grasp the full significance of the piece of art.For instance, the design shown in fig. 4 is used by a Turkish carpenter in most of his mosque doors. To him, this design is full of meaning because the number of its pieces is 99, the number of Allah's names. Other abstract meaning can be found in many other religions and spiritualities, as in Christian roman chapitels and gothic cathedrals.
PSYCHOACOUSTIC and PSYCHOVISUAL TEST
The test EAPAVE (for Experimentos de Acción y Percepción Auditiva,Visual y Estética, Experiments on Auditive, Visual and Esthetic Accion and Perception ) has been developped with the aim to measure acoustic and visual perception. This general concept covers from the abilities for acoustic-speaking-musical features as pitch, intensity, duration and timbre up to more composed and sophisticated structures, as musical motives or tolerated consonance for specific intervals. All tests find a threshold for the selected feature, measured as the value of its change interval for which the subject answers correctly half the questions ( of course the smaller the change, the more errors). He is asked to determine the direction of the change, which can be Up, Down and Hold -no change. This 50% threshold is evaluated after subtracting the random-answer bias.
 |
These measures can be made on large groups, with the purpose of calculating the median or expected value of a particular feature. This median value acts as a comparison background for the results of a given subject. For instance, the mean threshold for pitch interval in about one hundredth of that of duration, for the conditions of the experiment.
These conditions have a definitive influence on the results, for which they must be carefully planned, controlled and registered, for further consideration. Therefore there are instruction sheets for the operator, and different ones for the subject, all intended to avoid undesirable bias as much as possible. There are answer sheets to be filled in the test.
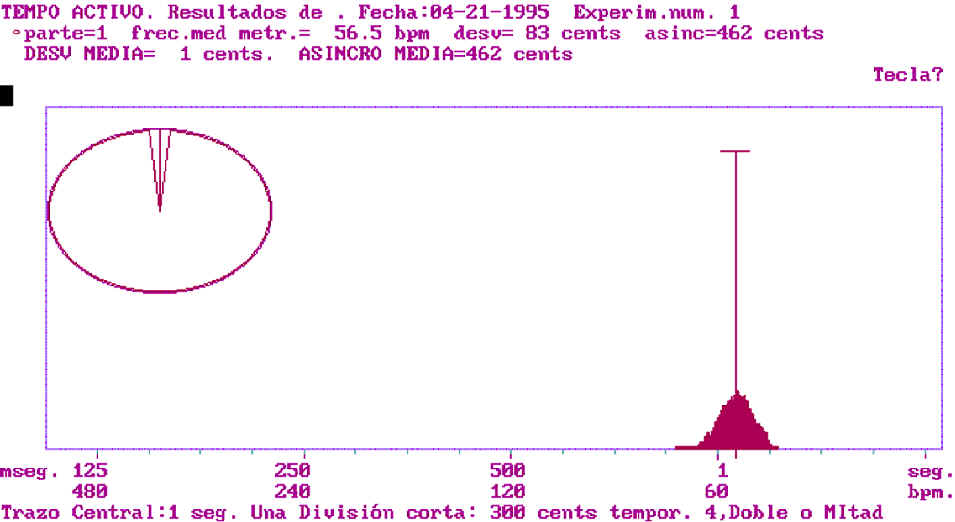
Abilities to perform are also measured, as well as to perceive. In particular the rhythmical proficiency is assessed, by means of the regularity in producing periodically repeated strokes. The computer keyboard is used for that purpose, using the screen to show the histogram of temporal intervals between strokes, roughly a Gaussian curve when logarithmic scale is adopted. The mean is taken as the intended duration value and the standard deviation as a value linked to the assessed ability, the smaller the better. Even patterns composed by different durations, rhythms, can be measured, showing interesting behaviors for each stroke depending of its situation in the rhythmic cycle; for instance, the first part is usually longer that its nominal and intended value. In the figure, the results for such action test are shown: the Gaussian curves representative of each stroke are drawn at the bottom in an logarithmic temporal scale. At the top a circle shows the relative duration between strokes, in a linear scale, similar to a pie-histogram. Besides, mean values of these durations and their standard deviation values are printed in numerical format.
In the wide world of Music, an intriguing and basic question is that of the music as a vehicle which carries, transports human expression and feelings in a sensible form. Although deprived of semantics, Music has been repeatedly qualified as a Language, and terms as speaking, expressing, saying are usually applied to some musics or interpretation of them.
In order to assess the quality and power of expression of music, some simple melody composing algorithms were written. They govern note pitch and durations according to a local reference and a general reference, with a set of parameter values as initial condition for departure.
The results - some of them included in two recordings: Vuelo por las Alturas de Xauen and Vuelo por las Alturas de Alhambra -, were surprisingly expressive, at least in the opinion of the author and some musicians near him. Very simple melodies in a modal ambiance were powerful enough to trig the improvising fantasy of the author, who did solos on several instruments, inspired by those automatic melodies.
All this proves, always in the opinion of the author, that the human mind and emotivity can find expression, even artistic and aesthetic ones, in controlled-random artificial artistic productions, provide they know, include, respect and wisely use the artistic properties that human taste requires. In the case of music, these conditions were primarily Numbers: simple integer numbers in the proportions between pitches and durations. The scales used Pythagorean conjoint intervals, i.e., 9:8 tones and 256:243 semitones, arranged in the modern Mixolidian (T-T-S-T-T-S-T) and the Indian Charukesi (T-T-S-T-S-T-T) successions.
The system was implemented in the 1982-85 years, on a MSD Intel machine with a 8080 microprocessor at 5 Mhz, and 64 Kbyte of Ram memory. The whole waveform was software synthetized and delivered through a D/A converter at its maximum rate of 30 khz. far beyond the specified one. Pitch was determined by sample rate, number of samples by period, and some routines whose execution took a short time which was added to the period to reach the machine cycle precision. With all this care, the tuning was very good, and it was improved even more by a piano-like emphasís, which is now modelized as a Pitch Perception Model.
Pitch Perception Model. -. We introduced a perception model to anticipate the impression that those frequencies are making in our ear and brain. Our Frequency-Pitch relation is related to the well-known Mel Scale, a mapping of physical measures into Pitch scale by an almost logarithmical function, with greater perceptual intervals in high and low sounds, a curve familiar to piano makers and tuners.
For practical purposes, that means that perceptual octaves correspond to a frequency ratio of 2:1 in the middle range (about 500 Hz.), but to more in the high and low parts of the keyboard, as much as a semitone more (ratio 2.05) in the extreme keys; and even more for sounds outside the range of piano (higher than 4000 Hz. and lower than 30 Hz, approx.).
We approximate this curve by a double potential function of the type
DCC ( f ) = k1 . | f - fc | k2
where DCC is the decrement in cents that the physical frequency 'f' suffers in the ear, 'k1' the "control wheel", or parameter that controls the effect of "sharpening" the scale, with 0 for a tempered or plain 2:1-octave scale; 'k2' is the power exponent. These constants have been empirically determined by asking to musically educated subjects, to choose between scales played on an electronic keyboard tuned according these function and constants; after repeated tests, over all in the high frequencies, the parameters for the selected scale are recovered from the computer. The result depends on the timbre and on the subject, but as a general conclusion, we can assume variations of 2-3 cents for the central octaves, and of 5-7 cents for the neighboring ones. That is, the physical intervals must be greater than the theoretic ones to satisfy the tonal sense, at both sides of central A.
AUTOMATIC MEASUREMENT OF ORIENTAL SCALES.
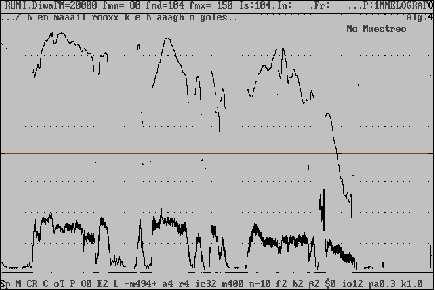
Oriental (Arabic, Turkish, Persian, North Indian, Byzantine, Flamenco) music cannot be adequately represented in the Western tempered scale, as is well known. The automatic measurement of oriental scales of maqamat and similar musical forms is a complex process, according to the complexity that these musical forms present. Pitch, Note, Interval, Scale, Consonance Structure and Maqam are stages of this analysis, assisted by correlative models of these aspects; we are far from tempered semitone scale recognition. The program ESCALA executes all those tasks on recorded or actual sounding music, by means of personal algorithms of pitch estimation and pattern recognition methods. ESCALA permits an accurate real-time measurement of pitch shades, with a careful notation in 53-degree/octave Hölder commas, in 72-degree/octave commas, or in almost exact Cents. Moreover, ESCALA can find the main consonances to estimate the modal tonic, and its related hierarchy. musical examples of those kinds of music, and their scale evaluation, will be presented during our talk, and our original pitch estimate methods will also be discussed.
The so-called Oriental Music in the West, employs a very rich and complex set of tones (pitches) and rhythms that are constitutive elements in this music; the tempering or rounding off those pitches impoverishes and converts it into tasteless stuff. The mastering of those shades of pitch, and their use in actual music (maqam, dastgah, raga), are a matter of time (a lifetime) which few persons, in the West or in the East, are disposed to or have the possibility of dedicating to it. However, only the person who does so, receives the richness of a Music which find its roots in the Past and blooms in the Present.
Music comprehension and enjoyment is a question of playing, communicating, receiving sounds and hidden meanings; but, from the músicological point of view, it is also very important to know the theory of the system and language involved in the music of a particular culture. The experts in the practice of this music (musicians, and some listeners) are able to pick up those shades of pitch, formerly described. But special conditions of listening and performance are needed, and no person can perceive all the shades in all the cultures: each listener always tries to understand a pitch as one of the elements of its own musical language (top of the list, the Western músicologist, who calls Do, Re, MI - c, d, e-, notes with other function, meaning and pitch).
We should not forget that in traditional music the tone, the note, is made by and for the finger, the vocal string and air pressure of the performer, much more than in the Western Music, where tone is fixed in the ear of musicians and listeners, as in many musical instruments (piano, organ, vibraphone, electronic instruments). As a conclusion, we can assume that Oriental Traditional Music is much more aware of pitch than Western.
The kind of music for which we intend our measuring tool to be useful, is primarily the cultured Oriental; in that wide concept we include: Arabic (A): Iraqi, Syrian, Egyptian; Turkish (T); Persian-Azeri (P); Andalusi-Mahghrebi (M); Bizantine (B); Oriental Christian (C): Armenian, Syriac, Maronite, Copt; Western Christian (G): Gregorian, Ambrosian, Roman, Beneventine; Indian (I): Pakistani, some Afghan; we include Spanish Flamenco or Cante Hondo (H) too; for a scale measurement alone we can work on any monodic music (Chinese, Japanese, Indochinese, Malayan, Javanese, etc.); and of course, all Folk (F) Music, which often sings free from the cultured framework. See, for instance [DomCardine, 1980; Danielou, 1959; During, 1991; Erlanger, 1949-1964; Gevaert, 1965; Guettat, 1980; Hakki, 1984].
To approach those various musical systems, a general code and a way to relate it to a specific music, are necessary, that is, a fine division of the octave, and a fine tool of measurement. This tool is valuable, not only to understand a particular kind of music, but also to know its tone system, establish its theory, and assist in its practice. This measurement must approach the perceived tone or pitch, rather than the fundamental frequency, a physical parameter not entirely proportional to it.
Pitch Estimation. - The automatic measure of pitch is not an easy task, first because pitch itself is an ill-defined concept, half physical (fundamental frequency), half a product of our perception. We do not know for certain if our inner ear analyses sound in time domain or in frequency domain, and in each case what is the range of our analysis, nor are we sure of our psychological decision about the tone or pitch that we attribute to a particular sound. What we know is that, in natural pitch estimation, fundamental frequency, frequency range (tessitura), frequency content (timbre), duration and intensity of the sound influence our decision, the first parameter being the more important.
Therefore, a frequency measure should not be sufficient for our purpose, musical notation and recognition, and several physiological and psychological considerations must be taken into account: we need, in brief, a model of our perception of pitch. This model has been refined and implemented in our laboratory, for both speech and music signals. First we shall consider the difficult task of frequency estimation.
Frequency Estimation. - After some years of research and development, we now have at our disposal a very efficient tool for pitch estimation, which we call ADA (for Auto-Disimilitud Adaptativa) [Sánchez,1977, 1979, 1993]. Briefly, for each short frame of the signal, we find out the delay for which the similarity between two short signal segments is greater, or minimal its dissimilarity. This delay correspond to the local period in the frame, if the dissimilarity is small enough (below a threshold); if not we will consider the frame as non-pitched. In mathematical language, the pitch P is the value of the delay
J for which the expression:2 f (t+J) - f(t) 2 ADS(f) = ))))))))))))))) is a minimum, below a threshold.
2 f (t+J) 2 - 2 f(t) 2
where the norm
2 f(t) 2 of the function f is its power measure over a time window w(t), whose time support (interval) is proportional (equal in our case) to the delay J. For digital (numerical) signals, this power measure is:2 f (t) 2 = 3 * fi *
that is, the sum of the absolute value of the samples, fi, extended from i=t+
J/2 to t+J/2.The function ADS (autodissimilarity), varies from 0 (perfect periodicity) to 1 (exact opposition), and equals .5 for random noisy signals. We have with it a measure of periodicity, setting the threshold in .3 for practical purposes (i.e., sequential analysis of musical or speech utterances).
Once we have a value for Pitch Period (in time units, milliseconds usually) we have also its inverse, Fundamental frequency, measured in Hertz, or Vibrations per second. the value is corrected with the Mel-like emphasis described before.
The values of pitch over a time interval can be stored to obtain a histogram of the pitches that have appeared during it. Some pitches will be more visited, showing the preference of the performer (or the instrument) for them: this histogram represents the scale, when the accumulated pitches show big peaks and valleys. If no peaks appear, we are then dealing with another kind of pitched sound, normally speech, where pitch varies continuously without strong preferences as in music.
Consonances research. - In our automatic system, therefore, we will first look for strong consonances, with some freedom in the tuning to accept little variations of style, on one hand, or minor errors of tuning, on the other. As we do not know, exactly, the interval ratios, we can not impose it on any music. As the octave is widely used in almost every scale, it will be not considered: only perfect fifth and forth, and also major and minor thirds will be looked for (in addition, for the frequency method, the second harmonic will appear at octave interval of fundamental).
The refered Mel emphasis is subsequently imposed on the measured intervals to be taken as the theoretic ones: thus a perfect octave in the 200-800 Hz area must measure about 1203 cents, and a perfect fifth, about 703, while towards the higher and lower frequencies, these measures should be 1207 and 705 approx.
The estimation of these consonances must necessarily be an approximate work, as no exact interval can appear, and what is more, we do not know what an exact interval is (see our perception model). A strong consonance will be, then, an interval which measure approximates of that which we consider a perfect interval: let us take exact numerical ratios as those references. If we have, for instance a fourth, ratio 4:3, very approximately 498 cents, we shall consider an actual interval as a fourth, when its measure is within a small range of error. However and again: "When and what is 'small'?" Our answer can be reached from our previous hypothesis: as the main consonances are easily perceived, they are rigid and admit a small range: let us say 10 cents. But lesser consonances, or dissonances, will admit a greater range, about 20-30 cents. Of course, when we approach these limits, we approach a bad or mistuned interpretation too.
The model formerly described has been built in ESCALA to recognize the complex musical phenomena of Oriental, Natural or Traditional Music, following the perceptual model also described. For music not conforming with these natural models (i.e., with no consonance requirements), only the scale, or list of notes, is offered. Not only pitch information is available from ESCALA: Intensity and Timbre parameters are measurable too, for a better characterization of the sound source.
For musics which do not admit clear consonances (if it exist), as the well-cited Slendro and Pelog of the asían South-East, these consonance limitations must be relaxed, in order to know first their intervals, and after discover their "unity factor" other than consonance. But let us continue with consonance-patterned music.
The notes which form the main consonances will be the main notes of the maqam; and probably the most intense in the histogram will be the modal tonic (the king) or the second one in importance (prime minister). These primary selections are needed because the same (or very similar) interval sequence can fit to different maqamat, changing only the references or main notes (Arabic Segah and Rast, Turkish Husseini, Ussak and Baiati, Turkish Ajam asíran and Chahargah, etc). See [Erlanger, 1949-1964; Guettat, 1980; Hakki, 1984].
Once the consonances are found, we must select the probable genera scopes, that is, the chain of tetrachords and pentachords forming octaves. Inside these scopes we will be able to detect the inner note intervals with the extreme notes, and from these intervals, to deduce the appropriate oriental name for it (see Appendix 1 for this attribution). The process is similar to the choosing a "nai" out of the set of seven, to play a melody: the player must recognize the intervals in the melody and contrast with those emitted by each flute. If besides and below a pentachord, we find the sequence tone-three quarter-three quarter inside a tetrachord, we should name the genus Rast, and make it begin in note rast (or naua) and finish in chahargah (or kirdan); and so on. We see how the estimation of the genus is paired with the name attribution to notes.
For irregular genera, that is, those whose extreme notes form not just intervals, as Saba or Huzzam, within different kinds of non consonant fourths, we must recognize before the main consonances, like the minor third which is present in both; and after see if the other notes fit into the pattern .
The process uses the information available in the set of selected tones, and crosses it with the stored models of maqamat; if two o more notes appear in the same zone (i.e. 'ayam and 'iraq, arabic B
= and B=*), it will reinforce a classification: if 'ayam and 'iraq appear together with an important peak at rast, and dukah, segah,..., the maqam Rast will be selected. Furthermore, if the pitch of segah is high, i.e., E-, it will be considered Turkish or Iraqi, meanwhile if it is E=, or even E=*, an Egyptian origin will be suggested.The more we want to recognize, the richer the model must be, taking in account finer shades of pitch and hierarchy: if a maqam going further in the taxonomic tree must be picked up, the necessary information should be stored in a way easy to recover and use in the recognition process. This storing of information is limited for the moment to the main maqamat of Arabic and Turkish music.
Electronic Tuning -. Besides the measurements of scales, ESCALA is able to tune an electronic instrument, as keyboards, via MIDI interface. So, the user can reproduce the heard music on the keyboard, contrasting the effects of natural and measured tunings. The tuning itself is done by changing the pitch attributed to the note, permanently in the cases where it is possible, as for tunable DX7-II and its family; or by means of Pitch Bend parameter, if not.
HUMAN and MECHANICAL RECITATION MODEL FOR PERSIAN METRICS
Poetry reciters and their machine counterparts share the same problems: where (ie. when) to place the emphasís and how to situate the product of speech in time, by the application of a whole package of rules that the human being acquires unconsciously through hearing and imitation, but that should be explicitly defined in the case of the machine, a fact that makes it necessary to minutely scrutinize all aspects of the synthesis. This package of rules is, in sum, a recitation model, and it must be a productive one, since it should actually create poetic speech. We will apply this model to a quantitative metric system, represented by Persian (Fârsî). Here we re-unite activities that are usually carried out separately, such as the abstract metric scheme of the scholar, with its synthesized recitation, and prosódic intonation with its automatic measurement. This establishes once again the essential unity -which never should have been broken up- between Humanities and Science, and could thus probably be considered as being of some interest.
Prosody is a major aspect of speech, partially reflected by punctuation in writing. Within prosody itself, it is the intonation that reveals, guide and gives life to syntax, the accents, the phrase modality, pragmatics and thus the fine nuances of meaning. A useful speech model, especially one that uses an automatic system of synthesis, must grasp and include the complex rules that govern prosody, especially intonation. With yet another turn of the screw, metrics adds a new component, an artistic one in this case -also only partially understood- which further complicates the model and its application to automatic synthesis.
We have tried to elaborate a partly common model that would make possible the generation of poetic speech, that is, speech with an artistic metrical scheme, from written text. All the prosódic traits of speech -pitch (height), timbre (phonetic value), intensity (volume), quantity (duration of the phonetic stretchs)- must be considered in order to produce an elocution faithful to a hypothetical ideal poetic speech, in a delicate balance and compromise. Moreover, the rules that control these traits have different temporal scopes (phrasal, syntagmatic, allophonic, etc.).
In the case of quantitative metrics, such as the Persian, it is the quantity proper that creates (marked versus unmarked) the metrics. The quantities of the syllables are here linked to the language itself, where the quantity is phonologically relevant (though it is true that this quantity is, in fact, accompanied by a certain phonetic change). The accent, meanwhile, has only a prosódic character (see above); diametrically opposed to Spanish, where the accent is phonological -not so the quantity-.
The criterion for deciding whether a syllable is long or short depends as much on how many allophones it contains as the kind of vowel -long or short- that makes it up. Generally the rule is: open syllables of the CV type are short, the V (the so-called motion) being short, like [ke]. All the others, such as [kî], [kie], [ken], [kîn] are long, that is, they include either a long vowel, or a diphthong, or are closed. Those of the type CVCC can even act as long or short in poetry, giving the last consonant a neutral quasí-vowel that we will represent as @.
In these metres composed of feet or clusters of longs and shorts, the syllabes are realized according to their relative quantities, that, in recitation, appear in the approximate proportion:
7 .1 ¯ = 3
In poetic recitation, we do not just get contrasts in emphasis -marks- between neighboring syllables -a phenomenon which falls within the competence of metrics. In close relation to this kind of recitation, there also exist regularities of these marks in time. Not only are metric patterns -feet- produced, but their production is organized in such a way that the marks tend to occur periodically.
This rhythmic periodicity takes us close, very close indeed to music, bringing in numbers into the production, something that has much to do with music. It means entering territory that leads us to the domain of the rhythmic period or measure, time intervals where things -notes, beats- happen. A place, however, where recurrences are sure to take place, where a punctual return is certain. That is, one knows and waits for the next bar's beginning.
The metrical schemes now fill in the bars, so that the durations added up, give a final result equal to the duration of the rhythmic period. Thus, a succession of feet such as:
/ ¯ ¯ v ¯ / v ¯ v v / ¯ ¯ v ¯ / v ¯ /
can be organized in such a way that, assigning the long and short syllables fixed and proportional durations, we should get regular rhythmic periods. For example, if - is equivalent to 2 beats, 7 to 1, and we begin counting from the second syllable and we count every 4 syllables, we get the regular scheme:
2 * 2 1 2 1 * 2 1 1 2 * 2 1 2 1 * 2
that admits a periodicity of 6 beats, transcending the verse limits: the beginning of the next one's first measure will occur "on time". The pause at the end of the verse will then take on the form of a rest that fills the void until the next bar. We have a 6-part measure that works throughout the poem, with oscillations in tempo, pauses, and fermata like its musical sister, but without breaking this numerical coherence known as rhythm:
q l qeqe l qeeq l qeqe l q . . q l qeq | first line of verse. . . . . . . . . . . . | second
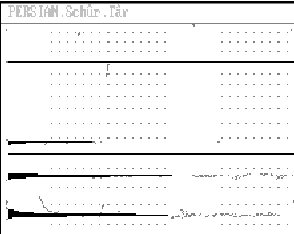
Jalâleddin Rûmî (Môulânâ). We have chosen a poem from his Dîvân Al-Kabîr dedicated to his spiritual guide-friend Shams-e Tabrîzî. The classical poems of a Dîvân (collection) have no punctuation, and therefore the verse itself acquires a syntactic function: each distich may include one or more clauses, coordinated or at least related in their meaning. In any case, the end of the line corresponds to a syntactic limiter ( , ; : . ) and the end of the stanza-distich (bayt), necessarily to a full stop. Let us take the first four:
Ízgfò ⣥±¾ z p£ ä bf }£¿À Ízgfò âZzZ® ¬À ä Ì }£²½ ®`` Zg ç`d ò xz®`` ã±` [£¥``ò }Z Ízgfò â£` £ Ú²`·`² y®``Á x£
|
Show me your face, for gardens and flowery fields I'm longing for. Open your lips, for sugar in abundance I am longing for. You Sun of Charm, come out one instant from behind the clouds, For that radiant, luminous countenance I'm longing for. With mischievous grace you said "Don't bother me any more, away you go!" That harsh "Bother no more,away you go" I'm longing for. That refusal of yours "Away, away! The master of the household is not in", That naughty gracefulness, the roughness on the threshold, all, I'm longing for." |
| (Translation: M.Puyâ) |
It becomes obvious, once the lines are heard, that they correspond to the metre Muzare' Musamman Akhrab Makfuf Mahzuf, also frequent in the poet Hâfez. The distich consists of two hemistiches of 14 versal syllables each (16 with the two rests [=2 shorts] at the end of the hemistich), grouped in feet that, according to metrical nomenclature based on the root "fa'l", and the common representation, station themselves as follows:
/ mus taf 'i lun / mu fâ 'i lu / mus taf 'i lun / fa 'al /
/ ¯ ¯ 7 ¯ / 7 ¯ 7 7 / ¯ ¯ 7 ¯ / 7 ¯ /
1 2 3 4 5 6 7 8
9 10 11 12 13 14
¯ ¯ 7 ¯ 7 ¯ 7 7
ben MÂ i rokh ke BÂGH o go les TÂN a mâ re ZÛST bog SHÂ i lab ke GHAN de fa râ VÂN a mâ re ZÛST 'ei 'ÂF @ tâ be HOSN @ bo rû NÂ da mî ze 'ABR kan CHEH re yê mo SHA' sha' e tâ BÂN a mâ re ZÛST gof TÎ ze nâz @ BÎSH @ ma ran JÂN ma râ bo RÔ 'ân GOF ta nat ke BÎSH @ ma ran JÂN a mâ re ZÛST vân DAF 'e gof ta NAT ke bo rô SHAH be khân e NÎST vân NÂZ o bâz @ TON di e dar BÂN a mâ re ZÛST
An iambic organization can be perceived; but here it is enriched by a subtle alternation of accentual pseudo-iambs: ¯ ¯, 7 ¯, 7 7. This scheme reveals the metrical and accentual arrangement that underlies and directs the poem, and to some extent guides its realization, its recitation in practice. Nevertheless, certain deviations can subsist, due to lexical, syntactic or expressive complications (e.g., we can have the following stress: [gof ti ze NÁZ ] (l.5) in order to emphasíze [NAZ], "mischievous grace"; or [ton DI e dar ban] (l.8), where [tonDI], "roughness", is pronounced with the stressed [DI] for being a noun). We see these deviations as reincarnations of the old distinction between abstract scheme and concrete realization (recitation), between rhythm and rhythmopoeia, between melody and melopoeia.
Automatic Analysis and Synthesis of Speech. Voice production model. prosódic traits must be measured in a reliable and consistent manner, preferably using automatic means; an initial recitation model thus emerges from this analysis. The only way to validate it, however, is to make it work: that is, implementing the model to generate automatic speech. This means that an artificial speaker brings the model into play, evaluating audience response. The results of the survey will probably suggest certain modifications in the model. The latter will be tested once and again until a satisfactory performance is achieved within a recurrent Analysis-Synthesis cycle. See our pitch estimation method in [Sánchez,1977, 1979, 1993].
The acoustic realization of a punctuated text -especially a poetic one- that is, the automatic synthesis of speech by means of rules, is very complex, due to the multiple levels, linguistic or other, that are present in every phrase, simple as it may be. Taking only the text, everything involved in it, in the form of letters and signs, must be recognized and norms of acoustic, sound, realization must be provided for these recognized suprasegmental elements and traits: the several pieces of information with acoustic relevance must be separated, in order to establish different chains for each type of information, as follows: 0. Orthographic Chain: includes the written letters, numbers and punctuation signs; 1. Lexical Chain: words that make up the sentence. Spaces are relevant, even phonetically. 2. Phonetic Chain: succession of symbols that represent allophones that realize phonemes (make them sound) involved in the written text. 3. Syllabic Grammatical Chain: chain of syllables with a view, principally, to the accentuation. The accented syllables must be emphasized mainly through the melodic traits (tonic accent), and to a smaller degree, by means of concomitant emphases on intensity and quantity. 4.5. Phrasal-Modal Chain: segmenting text into phrases or sentences, with the help of punctuation: full stops (.), question and exclamation marks (?!) are obvious segmentors. These signs provide the modality that, in turn, determines the corresponding suprasegmental intonation. 6. Syntagmatic Chain: the syntactic structure, suggested partly by the punctuation, also influences the accentuation since some words drop their accent when confronted with a more significant one: "cuánto más". 7. Accentual Chain: naturally, it has to do with speech accents, which coincide only partly with the written or orthographic ones. 8. Melodic Chain. 9. Intensive Chain. 10. Quantitative Chain: they realize through the pitch, intensity, and quantity traits, the phrasal, syntactic and accentual contributions. 9. Rhythmic Chain: there is a rhythm, not only in poetry, but also in normal speech, that lays stress on one of every two or three syllables: it must also be applied to the text by means of tone and quantity, in the manner developed in this paper. In this way, combining various information that proceeds exclusively from letters and punctuation, the written text is made to sound, to speak.
CONCLUSION
Computing by the human for the human can no longer be an activity separated from human flowing life. Technology and Humanities must grow together from now on: technology cannot develop without taking into account the human requirements and needs; Humanities cannot either grow without extensively using technological tools, as it has been always done. Now computers allow humanistic activities to use huge resources to help the finer human qualities express, learn and teach. We hope this paper has shown a small part of them.
Vuelta al Principio
Última
actualización:
martes, 07 de mayo de 2019 Visitantes: