El golpear una txalaparta (tabla o tablón, o sea pieza paralelepipédica de madera, generalmente) representa dos acciones diferentes pero simultáneas: Mover la tabla y deformar la tabla. El movimiento puede a su vez contemplarse como dos. desplazamiento paralelo a sí mismo y giro simultáneo, alrededor del centro de gravedad. La deformación sigue a la vez desde el punto del golpe.

Y todo esto considerando sólo una dimensión de la tabla: movimientos transversales, es decir, con eje perpendicular a la dimensión más larga (el largo) y paralelo al ancho. Consideramos pues : largo, ancho y grosor. El considerar igualmente los movimientos en el sentido del ancho, nos lleva, junto con los anteriores) a torsiones, que aquí no estudiaremos. de momento.

Los movimientos de desplazamiento y giro son absorbidos por los apoyos: en en el caso de la txalaparta se consideran apoyos libres, es decir que no tocan a la tabla, pero ya se comprende que de ser así, la tabla se movería y alejaría indefinidamente. Los apoyos pues entran a manifestarse como tales en el golpe, ya que al comprimirse por el movimiento de la tabla, pasan a ser más y más fijos, haciéndola rebotar, más o menos, en ellos.

Nótese que los golpes sucesivos al primero van a ejercerse sobre una tabla ya en movimiento, lo que añade complicación al tema.

En esto, como en todo el estudio, seguimos el antiguo, que no anticuado, Timoshenko. ya citado.

La determinación de la forma de vibración de una tabla golpeada pasa por varias fases:

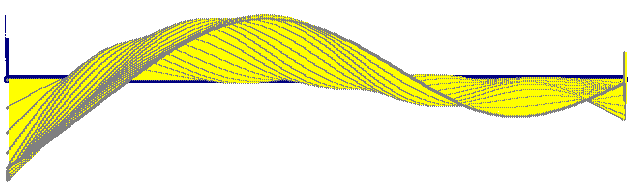
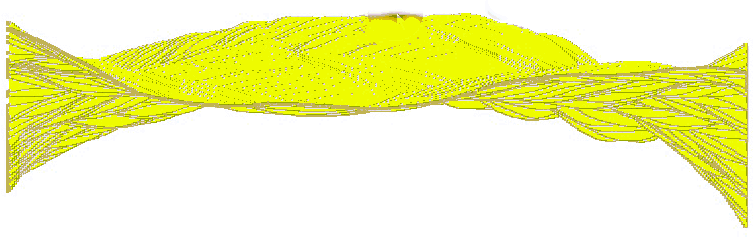
El resultado puede verse en la figura: golpe en el extremo izquierdo, vertical hacia abajo. Primero los primeros instantes. Más abajo, la huella de todas las oscilaciones, atenuándose lentamente.



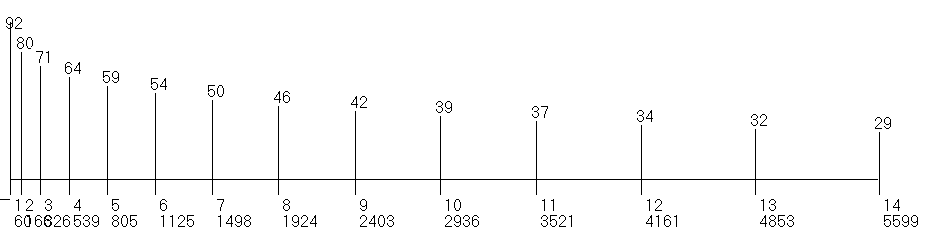
Arriba: Txalaparta vibrando y atenuándose. Abajo: Espectro de parciales (no harmónicos): peso y frecuencia.

Si se golpea en otro punto, se observa cómo la primera parte desplazada es la que sufre el golpe. propagándose después a cada lado y reflejándose (rebotando) en los extremos.

Golpe a 23% del extremo, mostrando forma casi inicial y primeros parciales con sus amplitudes y frecuencias.

Nótese que estas formas de la tabla en los primeros momentos del golpe se obtienen exclusivamente sumando los parciales de la tabla en proporción igual a su elongación --ordenada de la tabla-- en ese punto, y con dirección inicial de movimiento igual a la del golpe, y posición inicial en reposo --todos los parciales nulos en el momento del impacto: és decir, como se describe en los puntos 1 a 4 anteriores.

Las formas de impacto son verosímiles, es decir, se doblan en el punto del impacto, y luego la rigidez y elasticidad de la tabla, propaga la perturbación inicial por toda la tabla, reflejándose en los extremos, y continuando así indefinidamente salvo por la atenuación que van sufriendo todos los parciales --se supone por el momento igual para todos-- que lleva la tabla al reposo --eso sí, en tiempo teóricamente infinito.

Podemos considerar que el golpe puntual produce una velocidad en el punto golpeado. Es decir, produce un movimiento en el punto y no en los vecinos, no0 golpeado. Ente efecto es llamado, en tratamiento de señales (eléctricas) la función delta (aunque no es en rigor una verdadera función) cuyo valor es 1 en un punto y cero en el resto.

Analizando ese valor en frecuencias, es decir, hallando la transformada de Fourier de esa 'función' se obtiene como es sabido, la función Sinc que es

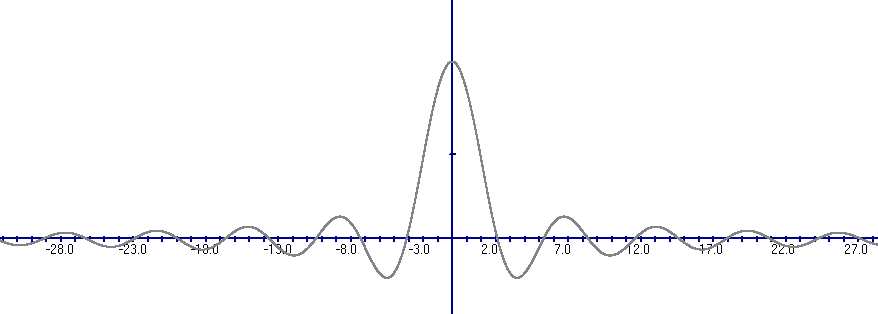
O sea, se aplica a la tabla en ese punto una infinidad de harmónicos que son vibraciones de la tabla con diferente frecuencia; pero sólo algunas tienen éxito, por decirlo así: aquellas compatibles con la longitud de la tabla, que son las que se refuerzan al reflejarse en los extremos: sólo quedan pues unos parciales (de frecuencias no harmónicas, múltiplos de un fundamentales, según de explica en txalaparta-vibración y timbre-2006B.

Se observa el aspecto de esta curva SINC en la envolvente de las amplitudes de los parciales, como en el golpe a 23% del extremo que representábamos más arriba. Hemos de fijarnos en ello porque tiene que ver indudablemente con la hipótesis de la señal delta aplicada a la tabla.

En las consideraciones realizadas hasta ahora se ha tratado siempre de un golpe puntual, que infundía velocidad (no desplazamiento) al punto de la tabla golpeado, y esa velocidad puntual de transmitía gradualmente al resto de la tabla, que vibraba.

Pero conviene ahora considerar golpes no puntuales, sino golpes anchos, por decirlo así. Por experiencia sabemos que lo agudo produce sonidos agudos (nótese el paralelo sinestésico). Es claro que un golpe estrecho produce más parciales agudos que uno ancho, porque intenta curvar la tabla con un ángulo más cerrado. En relación con este punto está también la dureza del palo golpeador, ya que una punta blanda se aplasta al golpear y adopta entonces una forma más ancha.

palo ancho y blando produce más parciales graves. Palo estrecho y duro, más agudos.

Podemos ahora intentar obtener un modelo de este golpe ancho: Una manera puede ser admitir que todo el ancho del palo golpeador impulsa con velocidad constante a la zona de tabla en contacto con él. Constante porque al momento de golpear la tabla abandona el palo, como ocurre con el golpe seco de una bola de billar. El hecho de que no supongamos que la tabla se desplaza instantáneamente al sufrir el golpe. debido a su inercia frente a la más débil masa del palo, no invalida esta suposición: se trata de modelos de fenómenos en los que siempre seleccionamos unos hechos y los simplificamos para poder resolverlos, en la suposición de que el resultado no es demasiado diferente. De hecho esto último se comprueba comparando los resultados obtenidos en el modelo y en la realidad.

En particular intuimos que bastaría estipular como condiciones iniciales sólo que los extremos de la zona ancha de contacto adquieren esa velocidad inicial.