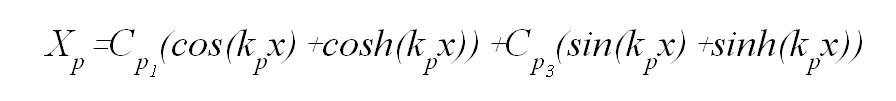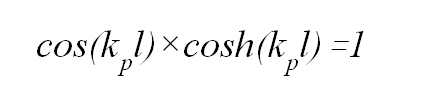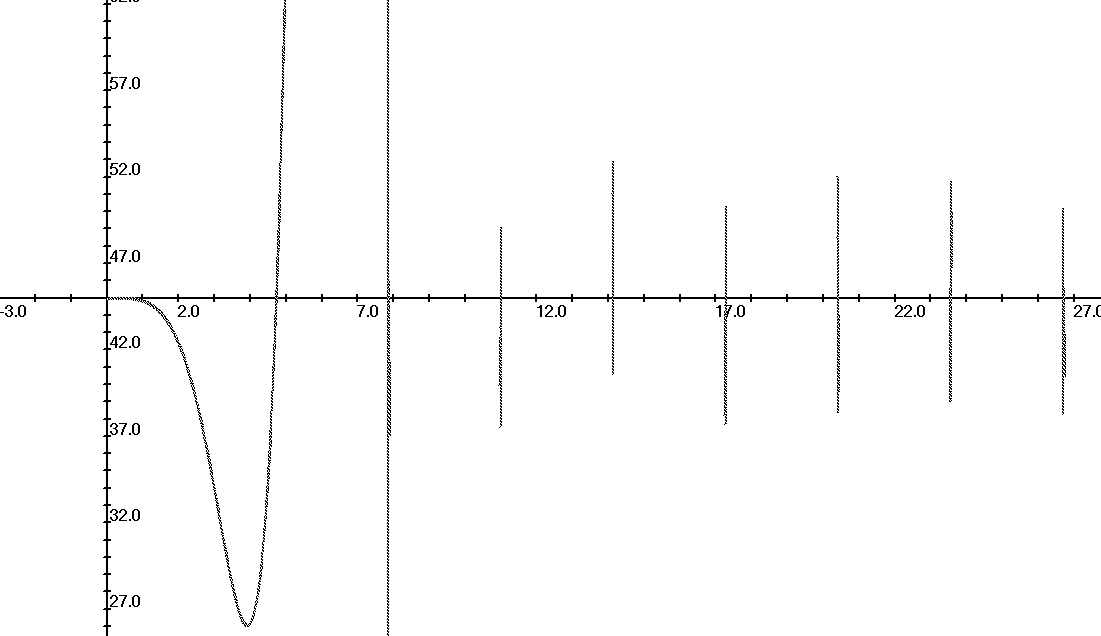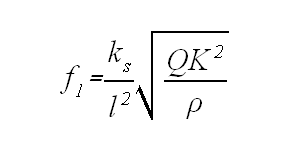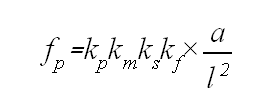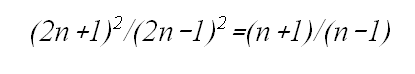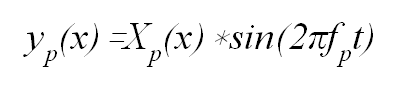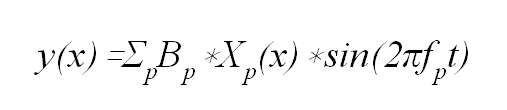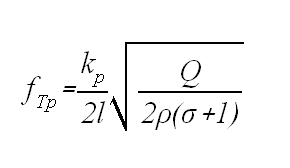Ahora
bien, como se conocen los radios de giro para varias formas, rectangular,
circular y tubular, y todas son proporcionales al grosor del tablón en la
dirección de flexión, en definitiva, la frecuencia depende, por un lado, de
las dimensiones longitud y espesor (l, a), y, por el otro, de
constantes que dependen del material (r , Q). Para parciales diferentes al
primero tenemos una constante adicional dependiente del parcial considerado
que llamaremos kp (lo que supone haber tomado k1 =1).
Si sacamos como kf fuera de la raíz el radio de giro K, que
depende de la forma de la sección, y agrupamos en una sola constante km
las constantes que dependen del material, encontramos la fórmula general:
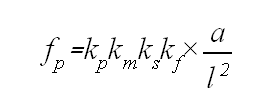
donde
las cuatro constantes dependen respectivamente del parcial considerado, del
material, del tipo de sujeción, y de la forma de la sección.
La fórmula anterior proporciona pues las frecuencias de los
parciales de una barra dependiendo de su material, de su forma y del modo de
sujetarla. Además, nos ofrece ya algunos interesantes comentarios para el
txalapartari:
1. Los sonidos de la txalaparta no dependen de la anchura de
ésta, sólo del grosor y de la longitud.
2. El sonido es más agudo (mayor frecuencia) cuanto menor es la
longitud, más corto el tablón, lo que es, y parece, normal.
3. El sonido es más agudo cuanto más grueso
(mayor a) es
el tablón, lo que a primera vista sorprende. Pero se entiende al recordar
que cuanto más grueso, más resistente es a la flexión, y la fuerza de
recuperación elástica es mayor.
Razones de las frecuencias.
Por lo tanto los parciales de vibración de un tablón tienen frecuencias no
armónicas entre sì, guardando proporciones sucesivas de 2.756, 5.4040,
9.933...
Primeramente se obtiene un parcial de frecuencia cero, es decir,
un desplazamiento único al golpear, sin vibración. Para los demás, aunque
las relaciones entre sus frecuencias no son estrictamente armónicas, puede
encontrarse esa armonicidad mediante la relación aproximada:
de
modo que la serie de números relativos 72, 92, 112,
132,..., se aproxima a esta otra: 3, 4, 5. 7, ..., sobre todo a
partir de números altos –por ejemplo 112--, que proporcionan
intervalos aproximadamente armónicos –algo estrechos-- entre parciales
sucesivos, según muestra la última fila de la tabla anterior, que lista esos
intervalos junto con el error en cents (centésimos de semitono) cometidos en
esa aproximación.
Así, se observa que los parciales impares –sin contar el 1–
guardan con el anterior una ley cuasi armónica, ya que sus relaciones son
las conocidas superparciales (n+1/n): 2:1, 3:2, 4:3, 5:4...., con un error
que decrece rápidamente con el orden del parcial p. Los pares guardan una
relación --siempre entera-- algo más complicada --(n+2/n)-- pero unos y
otros pueden ser aproximados en una escala de armónicos, creando un timbre o
un acorde, según los percibamos fundidos o separados como notas
independientes.
Por ejemplo, si consideramos sólo los parciales del 2 al 9, que
presentan relaciones de frecuencias entre
|
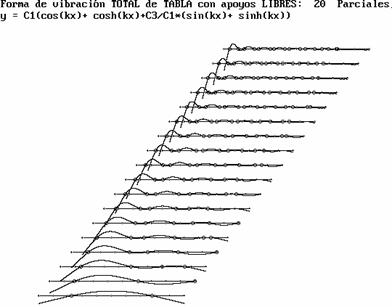
Fig.4. Vibración de la tabla mostrando la forma que
adopta sumando sucesivamente los 1, 2, 3, ., 20 primeros parciales de
la figura 3. |
parciales sucesivos aproximadamente iguales a 2:1, 5:3, 3:2, 7:5, 4:3, 9:7 y
5:4, observaremos que forman una escala de intervalos –algo estrechos,
repetimos-- de octava, sexta mayor natural, quinta justa, cuarta aumentada,
cuarta justa, tercera mayor alta y tercera mayor natural. Si tomamos el
segundo parcial (primero de los considerados en este caso, como DO, los
sucesivos serán DO, LA, MI, LA#, RE#, SOL y SI.
En todo caso la impresión
tímbrica es tonal o aproximadamente
tonal. La posición del primer parcial fuera de esta serie cuasi armónica
justificaría su supresión o situación tan grave que se separa
perceptivamente de los anteriores.
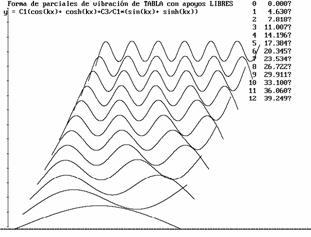
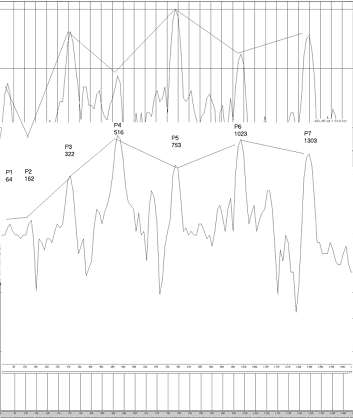
Numerando esos modos parciales de vibrar de acuerdo al número de
vientres, tenemos la serie de los parciales, de la que los 12 primeros son
representado en la figura 3, mostrando la posición extrema de cada uno, con
igual amplitud. En la figura 4 aparecen las formas del tablón vibrante
combinando sucesivamente del a 20 primeros parciales, todos en fase de
extremo izquierdo descendente, y con igual amplitud aproximadamente.
Vibración en el tiempo.
Cada parcial vibra senoidalmente, pasando a invertirse la curva tras
medio período de vibración; hay pues partes que en la vibración quedan
inmóviles, mientras que otras presentan máximo desplazamiento transversal:
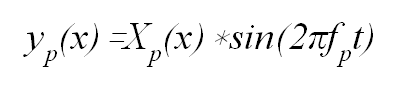
La vibración real de
un tablón será una combinación lineal de las vibraciones parciales
anteriores, dependiendo esa combinación de la forma inicial que adopta el
tablón golpeado, lo que depende a su vez del lugar donde y la fuerza
(velocidad) con que se golpea. Por lo tanto la
ordenada de un punto del tablón de abscisa x en el momento t es, en general:
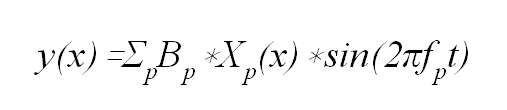
o sea
un sumatorio de todas las formas de los parciales, Xp, ponderadas por un
coeficiente Bp que depende de la velocidad que alcanza el tablón en el punto
en que se golpea y de su abscisa, c.
Esta suma equivale
a una composición de parciales similar a la harmónica de Fourier, donde los
parciales son senoides. Los parciales de la tabla se componen mediante una
suma porque estos parciales son independientes, es decir, la activación de
uno no altera la de los demás. A esta conclusión hemos llegado demostrando
la ortogonalidad de estos parciales considerados como vectores. Cualquier
forma del tablón vibrante sería un punto en ese espacio, siendo sus
componentes los coeficientes de cada parcial en esa vibración concreta;
coeficientes determinados por el punto de golpeo en el peso relativo de cada
uno, y , en amplitud colectiva, por la fuerza (traducida en velocidad del
palo transmitida al tablón).
|
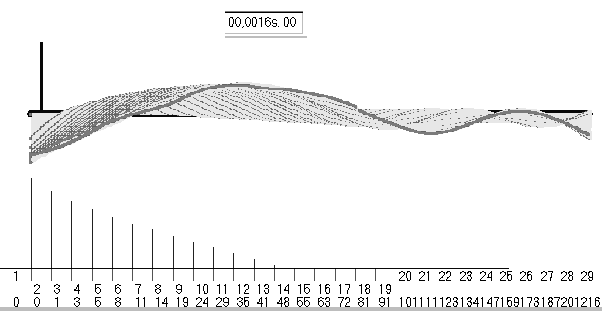
Fig.5. Simulación de la vibración de un tablón de 207
cm golpeado cerca de un extremo. Las líneas finas son las formas
anteriores, la gruesa la actual, a los 1.6 milisegundos del golpe. El
espectro aparece abajo. |
La ortogonalidad de
todos los parciales entre sí se ha demosgtrado empíricamente: es decir, se
ha ido calculando la integral de los productos binarios de estos parciales
(los 'cosenos' que forman cada par de vectores) y se ha visto que vale 1
para los productos de un vector por sí mismo ('ángulo' de 0º) y una cantidad
crecientemente pequeña a medida que dividimos el tablón en más segmentos con
lo que la aproximación a la curva teórica se hace mayor.
Hemos llegado a
unos productos cruzados de valor inferior a los 200db a los productos del
mismo vector por si mismo). De modo que si no es una demostración
matemática, si se demuestra que la activación de un parcial no activa a los
demás más allá de 200dB menos, algo despreciable. Problemas de cálculo nos
han impendido ir más lejos. En concreto hemos obtenido un valor de los
productos mixtos inferior al menos en 208.3 dB a los no mixtos, para un
número de segmentos de la tabla en el cálculo de
2069.
Vea el cuadro de
ortogonalidades de los 30 primeros parciales en el Apéndice 1.
Tipos
de sujeción.
Veamos ahora algunas tablas que nos permiten calcular las frecuencias
deseadas para diversos tipos de sujeción en los extremos.
Para
el tablón con sujeción de extremos libres, repetimos los valores relativos
al primer parcial, con el intervalo aproximado que respecto a él tienen los
tres siguientes (8º y 4º son octava y cuarta justas, 3ºM es tercera mayor y
q es un cuarto de tono) Se incluye además La situación de los nodos (puntos
sin vibración) y los vientres o antinodos (puntos de máxima vibración) son,
para esos cuatro primeros parciales:
Para Ks = 3.56
|
PARCIAL |
kp |
intervalo |
nodos |
vientres (aprox)
|
|
1 |
1 |
0 |
.2242 |
.50 |
|
2 |
2.756 |
8º+4º+q |
.1321 .50 |
.316 |
|
3 |
5.404 |
2.8º+4º |
.0944 .3558 |
.2251 |
|
4 |
9.933 |
3.8º+3ºM |
.0734 .2770 .50 |
.1552 .3885 |
Podemos cambiar la constante de sujeción para manejar números más cómodos: Para Ks
= .3926:
|
PARCIAL |
kp |
intervalo |
nodos |
vientres (aprox)
|
|
1 |
3.011
2 |
0 |
.2242 |
.50 |
|
2 |
5
2 |
8º+4º+q |
.1321 .50 |
.316 |
|
3 |
7
2 |
2.8º+4º |
.0944 .3558 |
.2251 |
|
4 |
9
2 |
3.8º+3ºM |
.0734 .2770 .50 |
.1552 .3885 |
|
5 |
11
2 |
|
|
|
|
6 |
13
2 |
|
|
|
|
7 |
15
2 |
|
|
|
|
8 |
17
2 |
|
|
|
de
modo que golpear en un nodo es evitar el parcial correspondiente, mientras
que golpear en un vientre, es hacerlo sonar con toda su amplitud. Todo
golpe, pues pondrá en movimiento cada uno de los parciales con amplitudes
dependientes de la posición de sus nudos y vientres: cada punto proporciona
una combinación de parciales única, un espectro: es decir, un timbre
determinado. Algunos puntos merecen especial atención:
El centro, C, que hace sonar máximamente p1 y p3, mientras que
p2 y p4 quedan omitidos.
El cuarto Q, cerca del nodo 1, a .22 del
extremo, que hace sonar p3 especialmente, suprimiendo p1, y haciendo sonar
algo p2 y p4.
El tercio T, que hace sonar especialmente p2, mientras que p1,
p3 y p4 suenan poco.
El Sexto, S, que hace sonar especialmente el cuarto, p4,
mientras que p2, p1 y p3 son pequeños.
De
modo que podemos individualizar cada uno de cuatro primeros armónicos
golpeando respectivamente en C, T, Q, y S.
Los radios de giro, para diversas formas de la sección y
parámetro a:
|
SECCIÓN |
kf |
a |
|
rectangular |
.29 |
grosor,
|
|
circular (barra) |
.25 |
diámetro, D |
|
anillo (tubo) |
.5 |
raíz (D2 + d2) |
Las constantes del material son:
|
MADERA |
km |
|
fresno |
450693 |
|
haya |
392232 |
|
corcho |
049799 |
|
olmo |
430331 |
|
abeto |
464420 |
|
caoba |
405190 |
|
arce |
437237 |
|
roble blanco |
408248 |
|
pino blanco |
365148 |
|
álamo blanco |
466252 |
|
sicómoro |
430331 |
|
nogal |
462910 |
En particular nos interesan aquí los modos de vibración de la
txalaparta de madera, rectangular, y los de la tobera, metálica, rectangular
o redonda, ambas vibrando libremente o casi. Por ejemplo,
TXALAPARTA de NOGAL: Se considera tablón rectangular, sujeción libre, f1
= (1 x 3.56 x 462910 x .29) x a / l2:
f1 = 477908 . a / l 2
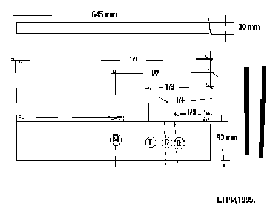
De
modo que un tablón de 2 metros (200 cm) de larga y 4 centímetros de grueso,
dará un fundamental (parcial 1) de 47.8 hercios, muy grave, aproximadamente
un SOL1, tecla 11 del piano.
Si se acorta el tablón a la mitad, la frecuencia queda
multiplicada por 4 (la longitud está elevada la cuadrado), o sea f1
= 191.161 hercios, SOL3 (algo bajo), tecla 35 del piano.
TABLÓN DE PINO: Un tablón de pino cuyas dimensiones son: 101.8 x 11.8 x
2.3--2.5 cm ha sido golpeado para comprobar la fórmula anterior. Las
frecuencias teóricas del primer parcial, y los tres siguientes, son:
f1 = (1 x 3.56 x
365148 x .29) x 2.4 / 102.82 = 87.30 para a=2.4
f2 = f1 x 2.75 = 240.6 f3
= f1 x 5.404 = 471.79 f4 = f1 x
9.933 = 867.19
Analizados los parciales realmente emitidos, se obtuvieron los siguientes
resultados:
|
PARCIAL |
frecuencia teórica (hz) |
frecuencia real (hz) |
desviación:6 % = 1 sem |
|
1 |
87.3 |
92.25 |
+6% |
|
2 |
240.6 |
240 |
-0.6 % |
|
3 |
471.79 |
472.5 |
+0.1% |
|
4 |
867 |
885 |
+2% |
Dada
la imprecisión en el conocimiento del grano de la madera, y en el grosor del
tablón, consideramos los resultados suficientemente exactos.
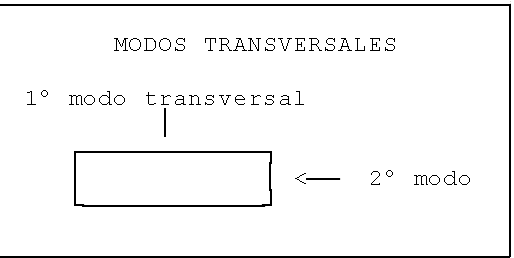
VIBRACIONES TRANSVERSALES COMPUESTAS.
|
Figura 6. Dos modos transversales de vibración en la txalaparta. |
En lo anterior hemos considerado una vibración transversal,
para la que contaban longitud y grosor, pero no anchura. Ahora bien, el
tablón también puede vibrar perpendicularmente a la dirección anterior: lo que
era anchura es ahora grosor, y lo que era grosor es ahora anchura (fig.6). A
poco que se golpee sesgadamente el tablón en una de sus caras, se pondrán en
movimiento los dos tipos de vibración transversal que comentamos. Ahora sí que
tiene interés la otra dimensión. Una juiciosa elección de ambas dimensiones
(cualquier proporción sencilla, como 2:1, 3:1, 3:2...) puede conseguir
timbres que podemos calificar de "diseño". En todo caso, se busque o no ese
efecto, estará presente, y ambos modos de vibración se darán en la txalaparta
real. Hay que hacer notar que la constante del material, km no será
idéntica, pues depende de la elasticidad, que varía según la relación del
corte a la fibra, en los materiales no homogéneos, como la madera.
VIBRACIÓN TORSIONAL
Un tercer modo de vibración, muy importante: como todos los
cuerpos, el tablón o barra puede torsionar, es decir, perder su carácter plano
y alabearse. Como experimenta una resistencia a ello, si es elástico volverá
a su posición de equilibrio, seguirá la torsión en sentido contrario, y así
sucesivamente: vibrará.
Este modo de vibrar se excitará cuando se golpea en
un punto lateral (ver figura, punto x) , tanto en sentido longitudinal, como
se hace para la flexión normal, como transversal. apareciendo entonces otra
serie de parciales, también armónicos, que dependen sólo de la longitud, de la
densidad y de los módulos de Young, Q, y Poisson, s. Sus frecuencias son:
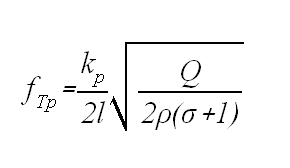
y pasando, como antes a calcular las cantidades bajo raíz,
obtenemos otra constante del material, k'm, que figura, para
algunos metales, en las tablas anteriores. Por su parte, kp se
reduce ahora también a la serie armónica 1, 2, 3,..: La barra se comporta
pues, también, como una cuerda o tubo, salvo la diferente significación de k'm
que depende en las cuerdas de la tensión y la densidad lineal, y en la
torsión, de la densidad y de los módulos de Young y Poisson.
Se observa (dividiendo ambas fórmulas) que las
frecuencias longitudinales y torsionales están en relación fija, relación que
depende del material, del llamado módulo de Poisson; puede calcularse que esta
relación es aproximadamente de cuarta (4:3) para el paladio, de tercera mayor
(5:4), para el acero y hierro forjado, y de tercera menor estrecha (7:6) para
el zinc.
VIBRACIÓN LONGITUDINAL
El cuarto modo de vibración para una tablón o barra es el
longitudinal, en el que en lugar de flexionarse transversalmente, sufre
alternativas expansiones y compresiones, producidas por un golpe sobre el
extremo, perpendicularmente a las otras dos direcciones transversales.. Si se
golpea en la dirección longitudinal, aparece entonces otra serie de parciales,
ahora armónicos, que dependen sólo de la longitud y del material:

obteniéndose la fórmula de la derecha, calculando, como para
las transversales, las constantes del material bajo raíz. Ahora k''m
es la misma constante del material que antes, excepto que debido a la no
homogeneidad del material, por ejemplo en la madera, no será ya idéntico. Por
su parte, kp se reduce ahora a la serie armónica 1, 2, 3,..etc. La
barra se comporta pues como una cuerda o tubo, salvo la diferente
significación de k"m que depende en las cuerdas de la tensión y la
densidad lineal.
ANCHURA DEL TABLÓN
Veíamos más arriba cómo la anchura del tablón (dirección
perpendicular a la de flexión, el espesor) no influye teóricamente en las
frecuencias emitidas; pero otra cosa es la radiación al exterior de esas
frecuencias. Para esto sí hace falta una cierta superficie, sobre todo para
radiar las más graves, al igual que ocurre en los altavoces e instrumentos
graves que son grandes. Creemos pues que hacen falta tablones anchos para que
los parciales graves cobren importancia, se oigan: de lo contrario se
desaprovechan las posibilidades de una txalaparta grande, porque sus
frecuencias graves, presentes, no son radiadas al exterior, no se oyen. Por
otra parte, cuanto más ancha sea la txalaparta, más aumenta el balance posible
entre vibraciones de flexión y de torsión, es decir, aumenta la paleta
tímbrica del instrumento.
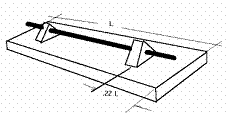
|
Figura 7. Posible sujeción de una barra metálica (tobera) en un tablón
radiante. |
Algo similar ocurre en las barras metálicas
(toberas). Una
posibilidad de hacer audibles las bajas frecuencias consiste en trasmitirlas a
un tablón ancho y hacer que éste las radie al exterior. Se trata de una tabla
armónica, como la del piano, o violín. Para ello hay que fijar de alguna
manera la barra al tablón, y esto obligaría a suprimir algún modo libre. Lo
lógico es fijar el tablón por los nodos del fundamental, hacia un quinto de su
longitud. por ambos extremos, por medio de un puente que sujeta, no basta
apoyar. Si se elige además una tablón con modos de vibración similares (igual
longitud), las bajas frecuencias de la barra serán amplificadas por el tablón,
radiando muy eficientemente. Experimentos efectuados por nosotros muestran que
en efecto, así sucede, oyéndose bellos graves.
SUJECIÓN DEL TABLÓN
Hemos visto cómo influencia el modo de sujetar la txalaparta a
los parciales, y por ende, al timbre emitido. En principio es simple, como
ocurre en las cuerdas: la inmovilización del tablón en un nodo de un parcial
(permitiendo su giro, claro está) no afecta a dicho parcial, pero sí a los que
no tienen nodo, bien sea un vientre, supresión máxima, o lugar intermedio
(supresión parcial). La vibración libre permite todos los parciales, pero es
una situación ideal: el peso del instrumento tenderá a apretarlo contra el
apoyo, por blando que sea; se intentan, como decíamos, apoyos que aproximen la
sujeción a la libre
Una posibilidad sería colgar el tablón de modo que
su peso no apriete el tablón contra el apoyo en el sentido de su vibración
transversal: ello se conseguiría colocándola vertical, con su anchura
perpendicular al suelo. Se golpearía entonces horizontalmente, vibrando en esa
dirección, mientras que el peso iría en vertical, sin interferirse. La
sujeción resultaría así libre, para la dirección de vibración.
Por último, puede emplearse musicalmente, durante
la ejecución, la influencia de la sujeción en el timbre: colocando una mano en
lugares específicos, incluso presionando más o menos, pasaremos de una
sujeción a otra, modificando el sonido, el timbre de la txalaparta. Estos
contactos momentáneos se realizan en tambores, variando tono junto con timbre,
y en cuerdas (como en el salterio persa, o santur), para modificar
tono-
|
|
|
Fig. 8. Atenuación de parciales según el lugar de golpeo: 1. Centro
(arriba): se atenúan pares. 2. A l/5 del centro (abajo): se atenúan
impares. |
GOLPEO Y VIBRACIÓN DE LOS PALOS
No sólo influye en el timbre emitido por el tablón el lugar de
golpeo, como se ha visto. También la forma de golpear influye. Naturalmente,
cuanto más fuertemente se golpea, más fuerte es el sonido. Pero además, esa
fuerza, más repentina, más veloz, crea una deformación más brusca en el punto
de impacto, originando flexiones de más arista, podemos decir, lo que
corresponde a parciales más agudos: como ocurre en la cuerda, la forma de onda
creada al pulsar, da lugar a un reparto armónico más o menos desplazado hacia
el agudo. Por igual razón, un palo fino producirá deformaciones más agudas y
parciales más agudos, mientras que un palo ancho y redondeado, pondrá en juego
parciales más graves.
Por su parte, los palos que golpean el tablón son
golpeados asimismo por él: es un choque en el que todos reciben un golpe. Por
lo tanto los palos suenan, y ese sonido pertenece al sonido total de la
txalaparta. Como tales barras percutidas longitudinalmente, emitirán parciales
que, como se vio, son frecuencias armónicas. Aquí también influirá el lugar de
sujeción: se potenciaran las frecuencias con nodos en ese lugar, a costa de
los que tienen un vientre.
VIBRACIONES COMBINADAS y RIQUEZA TÍMBRICA.
Según la dirección, lugar y modo de golpear el tablón o barra
encontraremos una combinación única de modos de vibración y de parciales que
hacen cada golpe irrepetible; esto sin descender al detalle, permite acercarse
al hecho sorprendente de que un instrumento tan aparentemente simple,
interese: incluso olvidando la rítmica y la dinámica del toque de la
txalaparta, tenemos una tímbrica muy rica, a cuyos fundamentos físicos hemos
querido acercarnos en este breve estudio.
Las consideraciones anteriores podrán, esperamos,
junto a un aporte a la comprensión del instrumento, sugerir a los txalapartaris nuevos
modos de construirlo y tocarlo, es decir, a desarrollar este interesante
instrumento vasco, para cuyo conocimiento y desarrollo esperamos sea útil el
presente escrito.
BIBLIOGRAFÍA
Backus, J. (1977) The Acoustic Foundation of Music.
Norton, N.York.
Beltran, J.M.
(1988)
"Txalaparta”. Cuadernos de Etnología de Navarra, nº 52. Pamplona: 419-439.
(1985) (ed.) "Euskal
Herriko Soinu Tresnak” /(“Instrumentos Musicales del País Vasco”). Gobierno
Vasco. Grabación en Compact Disk: L.G.55-1166/91-KD.1991: pista 9.
(1996)
Soinutresnak Euskal Herri Musikan (Los Instrumentos de la Música Popular
Vasca).
Orain,
Donostia. (en euskera)
Bucur, V. (1995), Acoustics Of Wood, New York, Crc
Press.
Goiri, J. (1996). Txalapata, Txakun, Los dos sonidos del
corazón, Arrigoriaga (Bizkaia).
Mercier, J. (1962), Acoustique, vol I, Paris, P.U.F.
Olson, H.F.
(1957), Acoustical Engineering, Toronto,
Van Nostrand.
(1967), Music, Physics and Engineering,
New York, Dover.
Randall, R.H. (1951), An Introduction to Acoustics,
Cambridge (USA), Addison-Wesley.
Roederer, J.G. (1979) Introduction to the Physics and
Psychoacoustics of Music.
Springer, N.York.
Sachs,K. (1966) Musicología Comparada. Eudeba,
B.Aires.
Sánchez González, F.J.
(1992) "Number as
Music Builder: Sonance".
Symp.
Mús.Informática y Psicoacústica. Delfos (Grecia).
(1993)
“Psicología del Ritmo Turco y Árabe". Symposium Multidisciplinar sobre Ritmo.
Cátedra Salinas de Musicología. Universidad de Salamanca. junio.
(1995a) “Teoría preliminar de la
sílaba”, Lenguajes Naturales y Lenguajes Formales XI C. Martín Vide (ed.)
Barcelona: Promociones y Publicaciones Universitarias: 569-578.
(1995b) “Txalaparta. Breve estudio
Acústico-Musical”, Txistulari, 162, pp. 19-24.
(1998) "A numerical
theory of rhythm applied to Oriental music analysis". Proceedings of 6th
ICEMCO, A. Ubaydli (ed.), Univ. of Cambridge.
London.
Sánchez
González, F.J. y Beltrán Argiñena, J.M.
(1998), “Una teoría numérica del ritmo aplicada a
la Txalaparta”, Txistulari, 173, pp. 27-43.
Schloss W.A.(1985) On the automatic analysis of percussive
music Rep. Nº. STAN-M-27. CCRMA. Stanford (Cal.)
Timoshenko, S.
(1929) Vibration problems in Engineering.
Van Nostrand. New York: pp.290
(1950) Resistencia
de Materiales. Vol. I y II.
Espasa.Calpe. Madrid.
Tobias, J.V. (,1970) Foundations of Modern Auditory Theory
Ac.Pres N.York.
Winckel, F.
(1960)
Vues Nouvelles sur le Monde des Sons.
Dunod,
Paris.
(1967)
Music, Sound and Sensation. Dover, N.York
Wood, A.B. (1944), A Textbook of Sound, London, G. Bell
and Sons. pp.111-118..
Zuaznabar. M.y P. (1975) En Antología de Instrumentos
Vascos L.P. Columbia- BC3896. S. Sebastián