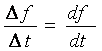El sonagrama (incluido en Conversaciones con Vicente Fuentes)

Primitiva (1949) pero eficaz manera de ver un timbre cambiar en el tiempo. Matemáticamente se trata de una transformada de Fourier a corto plaza (short time spectrum). Su cálculo suele hacerse ahora en digital, mediante el algoritmo rápido de cálculo llamado FFT (Fast Fourier Transform), ya encontrada en los 60', que devino el paradigma del tratamiento de señales. Y en vez del aparato original, que ocupa casi un metro cúbico, se emplea un programa de ordenador personal que no ocupa apenas nada. pero el principio es el mismo y el mérito del inventor. Se diseñó para visualizar el habla en principio, pero también la música y otros sonidos quedan muy bien representados en él.

El sonagrama representa ese espectro cambiante en coordenadas perpendiculares: tiempo, abscisa, creciendo hacia la derecha; frecuencia, en ordenadas, creciendo hacia arriba. Así podemos contemplar entidades frecuenciales, de tono (pitch), como líneas que evolucionan en el tiempo. Por ejemplo, es típica la visión de los llamados harmónicos de un sonido musical apareciendo y desvaneciéndose, subiendo y bajando a medida que la imagen se desplaza a la derecha. Esta representación refleja bastante bien nuestra impresión o percepción de algunos fenómenos, como la altura musical.

Pero mucho de lo visto es una preparación, una adecuación de los parámetros de análisis para que en efecto reflejen nuestra impresión, o impresiones, pues son varias.

Necesitamos ahora concretar esos parámetros y sus valores para un reflejo deseado. Los dos principales son la frecuencia de muestreo (Fm) y el número de puntos de la FFT, parámetros muy ligados que van a determinar el aspecto del sonagrama.

En la tabla siguiente se ve esta relación: una FFT corta, de pocos puntos, o sea, muestras utilizadas en su cálculo, precisa (y representa a) un corto intervalo de tiempo

Por ejemplo a 10000 hz, 10000 muestras por segundo, 100 muestras representan  un décimo de segundo (regla de tres), o sea 100 ms.

Pero por otra parte, esa FFT obtiene en su calculo, 100 valores de frecuencia, valores que son la amplitud en 100 bandas de frecuencia iguales que cubren el ámbito de fr4ecuencia total: la frecuencia de muestreo: Luego esos 100 valores son 100 bandas de frecuencia cuya anchura es 100 hz. Es un espectro de tipo momentáneo, instantáneo en tiempo, pero amplio, difuso en frecuencia.

Si por el contrario, usamos 1000 puntos en la FFT, representan por un lado 10 ms solamente, pero por otro divide el rango de frecuencias (10000) entre 1000, o sea 10 hz por banda. Es un espectro de tipo amplio, promediado en tiempo, pero preciso en frecuencia.

El caso es representado en la tabla, cuya primera columna es corta en el tiempo y ancha en frecuencia; la tercera se comporta inversamente, y la del centro es un compromiso.

El compromiso a tomar en la práctica depende de los que pretendemos: depende del espesor frecuencial que consideramos, por un lado: y por el otro, de su variación temporal: si el fenómeno es estrecho, preciso en frecuencia, como un harmónico, y varía lentamente en el tiempo, es claro que una transformada fina (de muchos puntos) representará adecuadamente el fenómeno, ya que el alto promedio temporal ocupa pocas bandas debido a la pequeña variación. Si por el contrario en fenómeno es ancho en frecuencia y muy variable, como formantes en el habla, una transformada de menos puntos es recomendable.

De modo que, elegido el fenómeno y su variación, deberemos elegir

 una cuadrícula temporo-frecucncial cuya relación de tamaños sea similar a la pendiente de la curva incremento en frecuencia por incremento en el tiempo.

Como I(f) es igual a Fm/N, y I(t)=N/Fm, tenemos que:

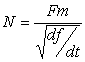
Por ejemplo, si queremos visualizar un harmónico de 100 hz. que varía una octava por segundo, elegiremos N=Fm/10. Si Fm es 44100 muestras por segundo, usaremos unas 4410, es decir, la potencia de dos más cercana, 4096 puntos.

Pero si queremos visualizar un fenómeno muy preciso en frecuencia que varía lentamente, como un harmónico  de 1000 hz que vibra un semitono unas 8 veces por segundo, tenemos:  Raiz2( df / dt ) = Raiz2(1000*1.059 /8) = 11, luego N=44100 /11, prácticamente lo mismo que antes.. Pero si el harmónico fuera de 100 hz, tendríamos 3 veces menos (raíz de 10), o sea, unos 400 puntos, 512 exactamente.

La variación de la frecuencia de muestreo, Fm,  cambia proporcionalmente todos los valores obtenidos. Si consideramos ahora no el incremento de frecuencia sino la frecuencia y el intervalo en semitonos, como el primero es el producto de los dos últimos, tenemos:

 

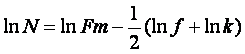
El problema se complica si promediamos en el tiempo las sucesivas transformadas. Pero lo dejamos aquí por hoy.

Hemos pues concretado un criterio para analizar mediante el sonagrama, es decir, mediante la FFT..

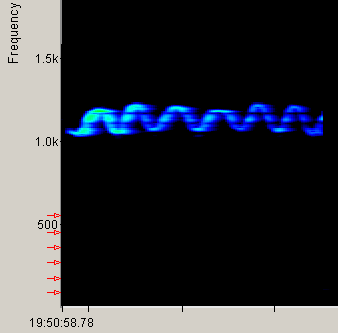
Vea ejemplos de su uso en Canto harmónico 2. Y veamos unos ejemplos de lo dicho: Un silbido trinado alrededor de 1000 hz.:

Silbido a unos 1000 hz. en trino de un tono

 

---

Vuelta al Principio  Última actualización:  Tuesday, 09 de July de 2013 Visitantes: