Algunas cotas no son alcanzables sin disminuir el ángulo diferencial. El algoritmo va y viene sobre el mismo lugar. Desde luego 1 mm como distancia media es muy poco en el contexto (huesos humanos) y está dentro de la 'vibración' (inestabilidad de la toma Kinect) inherente al kesqueleto. Y desde luego los saltos angulares de búsqueda no tienen que ser iguales a los diferenciales. Lo adecuado es usar valores decrecientes al acercarse al 0, como se hace por Newton-Cramer y similares. Si los movimientos entre incógnita y inicial son mayores , están más lejos (elegimos matrices absolutas de hueso 5 en lugar de 4), la búsyqeda dura más con iguales parámetros:
Cota mm 10 1 1 1 1 Salto º 1 .5 .3 .2 .1 Pasos 217 444 741 >1000 >1000
Hueso 4 5 Cota mm 10 10 1 1 1 Salto º 2 1 .5 .3 .3 Pasos 108 217 444 741 597
Como idea intuitiva de lo que hacemos, veamos el proceso sobre el plano y
en dos dimensiones con puntos. Si el punto A quiere ir al B y solo tiene
horizontales y verti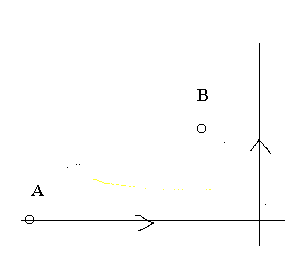
cales,
debe primero tomar la horizontal, que le acerca más deprisa al B, y al
llegar a 'su altura' torcer hacia arriba, salvo que la vertical más próxima
sea la que aparece en la figura, con lo que estará obligado a tomarla.
Pero apliquemos los conocidos pasos de Newton Kramer:
Tenemos un función de una o varias variables de la que queremos hallar el
mínimo si hay uno solo, o el más próximo a un punto de partida en ese
espacio de varias variables.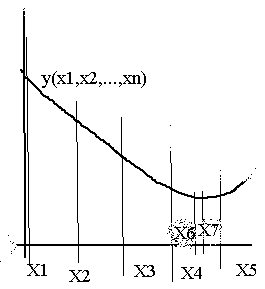
Si la función crece o decrece monótonamente, estamos seguros de que, una vez conocida la pendiente en el punto de partida, será la misma hasta que lleguemos al mínimo, si existe (puede ser una función infinitamente creciente o decreciente, como una recta o una exponencial, sin mínimos finitos)
En el caso de varias variables habrá que probar qué incrementos disminuyen la función, y de ellos, cuál es es el que lo hace más deprisa. De modo que cada vez que tomamos valores, comprobamos ese incremento óptimo. El proceso sigue hasta que en lugar de decrecer la función, empieza a crecer. Esto nos indica que hemos rebasado el mínimo y por tanto disminuimos el salto o incremento diferencial de las variables y repetimos la búsqueda. Ésta acaba, arbitrariamente cunado llegamos a las cercanía deseada del mínimo, definida por una bola de radio salto incremental de ángulo, para cada una de variables (una sola en en la figura). O sea en un elipsoide de varias dimensiones.
El salto incremental ha de ser pequeño para que estemos razonablemente seguros de que no englobamos el mínimo que buscamos, de que no abandonamos la pendiente en la que nos encontramos.
En la figura (mejorable, sí) a la izquierda, vemos el proceso: las abscisas son más bien puntos o vectores de todas las variables. Comenzamos por X1 y determinamos probando en las 6 direcciones incrementales de giro, cual es la más favorable. En esa dirección saltamos a X2, repetimos y vamos a X3, X4, X5; en ese momento observamos que la función y crece: hemos sobrepasado el límite. Reducimos el salto (por ejemplo, a la mitad, aunque hay mejores elecciones) y continuamos hasta llegar, o a una distancia cota máxima.
De esa manera el número de saltos se reduce drásticamente, de 500 a 15, por ejemplo. En amarillo mostramos dos buenos comienzos de búsqueda
Hueso (operadores) 4 Cota mm 10 10 10 10 10 1 Salto inicial º 1 10 30 60 90 60 Pasos 315 38 19 13 18 27
La rutina que lo hace, muy parecida a la anterior en II, es:
_____________________________________________________________________________________________________
Public Function reune_por_microaproximaciones_paso(ByVal pseudoskel_orig() As Point4D, _
ByVal pseudoskel_incog() As Point4D, angulo_salto As Double, cota_distan As Double) As Double
'Dim veces As Integer = 0
Dim pseudoskel0_1 = pseudoskel_orig
Dim distas, distas0 As Double '10 metros
distas = 1000
veces = 1
cuaternion_estimacion_total = Quaternion.Identity
otor_angulo:
MatrizBusqueda1 = contruye_mat_giro(angulo_salto, 0) : CuaterBusca1 = quat_de_matriz(MatrizBusqueda1)
MatrizBusqueda2 = contruye_mat_giro(angulo_salto, 1) : CuaterBusca2 = quat_de_matriz(MatrizBusqueda2)
MatrizBusqueda3 = contruye_mat_giro(angulo_salto, 2) : CuaterBusca3 = quat_de_matriz(MatrizBusqueda3)
While distas > cota_distan And veces < 1000 'milimetros
'elige la mejor
Dim quater = elige_el_mayor_gradiente(pseudoskel0_1, pseudoskel_incog)
'pseudoskel0_1 = realiza_una_microaproximacion(pseudoskel0_1, quater, pseudoskel_incog)
pseudoskel0_1 = realiza_una_microaproximacion_opciones(pseudoskel0_1, quater, pseudoskel_incog, 1, 1)
cuaternion_estimacion_total = cuaternion_estimacion_total * quater
distas0 = distas
distas = 1000 * distancia_pseudoskel(pseudoskel0_1, pseudoskel_incog)
veces = veces + 1
'retoco angulillo? si sobrepaso minimo
If distas > distas0 Then
angulo_salto = angulo_salto / 2
GoTo otor_angulo
End If
End While Dim dif_cuater = cuaternion_estimacion_total - cuaternion_incognita dif_cuater.ToString() if informa then presenta_cuaternion(cuaternion_estimacion_total) Return distasEnd Function
_____________________________________________________________________________________________________
Y obtenemos al cuaternión estimado (calculado) del cuaternión incógnita.
Podemos incluso calcular la dirección compuesta de las tres mejores y girar sólo sobre esa dirección. En principio suponemos que nos lleva al punto requerido, pero debemos comprobarlo.
______________________________________________________________________________________________________________________________
Nos preguntábamos ¿qué nos queda? 1. Añadir un cierto ruido (variaciones aleatorias a algunas articulaciones 2, Variar la distancia, es decir su tipo. (incluso distancias entre cuaterniones y matrices) 3. Añadir orígenes diferentes a cada imagen (translación diferente para cada uno, situación que se presenta con dos cámaras. 4. Operar con dos cámaras reales, diferentes y simultáneas. 5. promediar los operadores estimados sobre varios esqueletos (¿1 segundo, 30 imágenes?). Proyecto Danzante. Reunir imagenes.Estrategias. Giros y Escalados o viceversa.htm Proyecto Danzante. Reunir imagenes. Escalados.htm