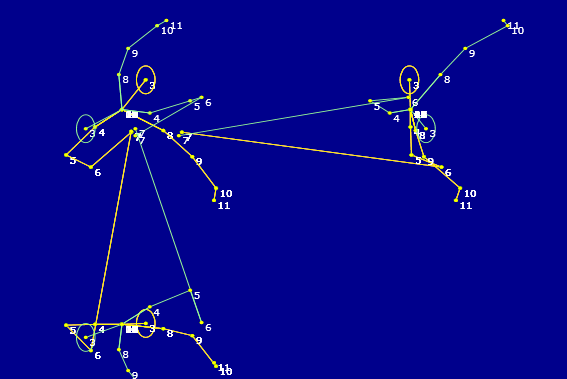
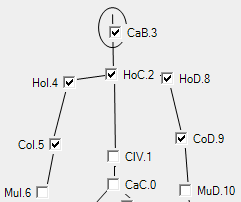
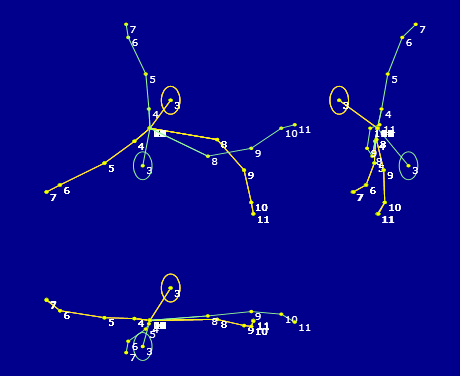
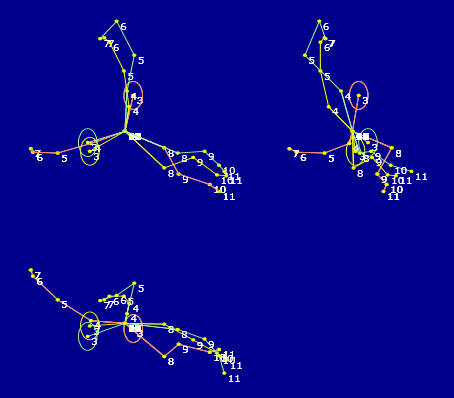
Es decir, el ruido 'desconcierta' al buscador, incluso con una desviación típica media de 10 mm (20, 50 10 en x,y,z). Vamos a limitar el número de puntos en la búsqueda (en concreto, para el cálculo de distancia en línea recta, cuerdas) para ver si la búsqueda es más segura y rápida. En efecto, cuando reducimos puntos a hombros codos y cabeza, converge. Son más fiables, lo que revalida lo citado en Comparación con ISTDK. Además se reduce el número de operaciones y de ahí, el tiempo de cálculo. Otro caso en que las articulaciones de manos y muñecas (y cabeza) desorientan al buscador (primer caso). Cuando reducimos a cabeza, hombros y codos, se converge, y se converge rápido (2º caso y figura). Asistimos ahora a una progresiva deterioracion de l la ingcógnita, lo que dificulta pero no impide la convergencia, siempre con esas articulaciones básicas. Cuando hablamos de deterioración, lo hacemos siempre en el contexto de la simulación. En el caso real de dos cámaras tenemos simplemente dos esqueletos. No hay ninguno más correcto que el otro, sino más bien dos esqueletos algo imprecisos que habrá que hacer converger. Ese proceso se repetirá varias veces (por ejemplo 100) para promediar los operadores sintetizadores 8que convergen los esuqletos en uno) obtenidos en cada uno de esos casos. Esta media (normalizada) será la que tomaremos como operativa a todo lo largo de la seleccion y eleccion de articulaciones y huesos para formar el esqueleto corregido, que tomaremos como correcto.
Dist: Ini= 526 65,0º | 22,0º Busca=04 mm| 19,0º | 10,0º
Res: 1 0.625 1
-0,461318731249129; 0,302114926409592; -1,04073711832618; 0,337317338716168
0,0425926704654612; 0,263927007480558; 0,922730686160967; 0,277662528912147
-0,39167701072271;0,256506972848058;-0,883625085741485148,037088356723
Dist: Ini= 523 64,0º | 21,0º Busca=06 mm| 19,0º | 09,0º
Res: 1 0.9375 1
-0,461318731249129; 0,302114926409592; -1,04073711832618; 0,337317338716168
-0,0263146674039252; 0,196898912078596; 0,941998675746143; 0,270512202301853
-0,39167701072271;0,256506972848058;-0,883625085741485148,037088356723
Dist: Ini= 526 65,0º | 22,0º Busca=01 mm| 19,0º | 10,0º
Res: 1 0.46875 0.1
-0,461318731249129;0,302114926409592;-1,04073711832618;0,337317338716168
-0,0227739039554768;0,201054394046745;0,944434323024267;0,259041096019179
-0,39167701072271;0,256506972848058;-0,883625085741485148,037088356723
Sin ruido Dist: Ini= 540 41,0º | 11,0º Busca=90 mm| 23,0º | 04,0º
Res: 1 0.078125 0.1
-0,461318731249129;0,302114926409592;-1,04073711832618;0,337317338716168
-0,0373218077656522;0,0998736170711611;0,845187141299383;0,523728020503477
-0,39167701072271;0,256506972848058;-0,883625085741485148,037088356723
Con ruido DT=10 Dist: Ini= 560 46,0º | 12,0º Busca=91 mm| 24,0º | 04,0º
Res: 1 0.078125 0.1
-0,461318731249129;0,302114926409592;-1,04073711832618;0,337317338716168
-0,0393779674692616;0,100574872036143;0,875845205999347;0,470350131200989
-0,39167701072271;0,256506972848058;-0,883625085741485148,037088356723
Ruido 10 Dos veces sucesivas Dist: Ini= 557 45,0º | 12,0º Busca=91 mm| 25,0º | 04,0º
Res: 1 0.0390625 0.01
-0,461318731249129;0,302114926409592;-1,04073711832618;0,337317338716168
-0,0382162344030577;0,0999769813898108;0,870839528433735;0,479773528175164
-0,39167701072271;0,256506972848058;-0,883625085741485148,037088356723Lo mismo pero con incremnetal=.01 grados sexa Figura debajo
A simple vista se ve la pobre convergencia
Dist: Ini= 210 126,0º | 06,0º Busca=01 mm| 104,0º | 00,0º
Res: 1 0.15625 0.1
-0,378224760284999;-0,0291025243106742;1,7611586811461;0,0786926626946378
0,847921494706488;-0,51658333962585;-0,0824792107766373;0,0858368908184747
-0,209944132619806;-0,0161541624584477;0,977579922161755174,997758298157
Con esas articulaciones converge tomando 30º a priori, Sin ruido Con ruido
|
Dist: Ini= 187 03,0º | 14,0º Busca=188 mm|
27,0º | 27,0º Resultados: Cota_distan: ángulo salto: 0.05859375 salto increm: 0.1 ruido: 10 Pasos: 30 Incog eje: 0,274408469698147; -0,0657865204295606; 0,959360268870716 Estim eje: -0,0336506864508215; -0,0843953912138723; 0,995863971254732 Incog angle:176,211378407309 Estim angle:176,211378407309 |
|
Curiosamente, la distancia menor a la que se llega es aproximadamente de la mitad a la tercera parte de la desviación típica impuesta al esqueleto incógnita. La rutina, muy robusta con esas articulaciones básicas y fiables, queda por ahora así: ____________________________________________________________________________________________
Dist: Ini= 197 114,0º | 120,0º Busca=06 mm| 84,0º | 85,0º
Resultados: Cota_distan: ángulo salto: 0.05859375 salto increm: 0.1 ruido: 10 Pasos: 88
Incog eje: 0,274408469698147; -0,0657865204295606; 0,959360268870716
Estim eje: -0,917311824354365; 0,397842914449204; -0,0161255177352645
Incog angle:176,211378407309
Estim angle:176,211378407309
Incluso ruido=40 (desvtip =40mmm, todas las coordenadas de todas las articulaciones), quedando eso sí a más distancia media mayor 2 cm. En la figura siguiente se aprecia ya una separcion entre buscador e incognita (amarillo y verde) lógica porque ya no son iguales. Dist: Ini= 312 103,0º | 111,0º Busca=20 mm| 78,0º | 79,0º
Resultados: Cota_distan: 1 ángulo salto:30 a 0.00732421875 salto increm: 0.01 ruido: 40 Pasos: 55
Incog eje:-0,882628910705969;0,457500643856379;-0,10797854813338
Estim eje:0,236555283722422;-0,810783158686658;-0,535417843682007
Incog angle:145,73800197824
Estim angle:145,73800197824
Dist: Ini= 313 103,0º | 111,0º Busca=32 mm| 77,0º | 80,0º
Resultados: Cota_distan: 1 ángulo salto: 0.00732421875 salto increm: 0.01 ruido: 50 Pasos: 49
Incog eje:-0,882628910705969;0,457500643856379;-0,10797854813338
Estim eje:0,681137103849455;-0,657116393342618;-0,322878137011422
Incog angle:145,73800197824
Estim angle:145,73800197824
Incluso 100 mm Dist: Ini= 311 106,0º | 113,0º Busca=55 mm| 83,0º | 87,0º
Resultados: Cota_distan: 1ángulo salto: 0.00732421875salto increm: 0.01ruido: 100 Pasos: 39
Incog eje:-0,882628910705969;0,457500643856379;-0,10797854813338
Estim eje:0,714329646402739;-0,635036032847364;-0,294044883063146
Incog angle:145,73800197824
Estim angle:145,73800197824
Incluso 140 mm y segumos probabdo (aguante 200) Dist: Ini= 319 113,0º | 119,0º Busca=60 mm| 92,0º | 96,0º
Resultados: Cota_distan: 1 ángulo salto: 0.00732421875 salto increm: 0.01 ruido: 140 Pasos: 63
Incog eje:-0,882628910705969;0,457500643856379;-0,10797854813338
Estim eje:0,20296046229761;-0,866059415230191;-0,456889636602845
Incog angle:145,73800197824
Estim angle:145,73800197824
'¡salto_incremental
'Intento con RUIDO Esto dunciona perfectamente sin ruido, converge rápido
Public Function reune_por_microaproximaciones_paso_controlado(ByVal pseudoskel_orig() As Point4D,
ByVal pseudoskel_incog() As Point4D, _
angulo_salto As Double, cota_distan As Double, salto_incremental As Double) As Double
'Dim veces As Integer = 0
Dim quater, dif_cuater, quater_sal As Quaternion
Dim pseudoskel0_1 = pseudoskel_orig
Dim distas, distas0 As Double '10 metros
distas = 1000
veces = 1
cuaternion_estimacion_total = Quaternion.Identity
Call inicializa_quat_incre(salto_incremental)
otro_angulo:
Call inicializa_quat_salto(angulo_salto)
'SI HAY RUIODO, HABRÁ QUE ^PONER OTRAS DETENCIONES AUTOMATICAS
'Por estabilidad de valores por encima de la cota de fin
parado = 0
While distas > cota_distan And veces < 1000 And parado = 0 'Then ''milimetros
'elige la mejor
quater_sal = elige_el_mayor_gradiente_incremental(pseudoskel0_1, pseudoskel_incog)
'pseudoskel0_1 = realiza_una_microaproximacion(pseudoskel0_1, quater, pseudoskel_incog)
pseudoskel0_1 = realiza_una_microaproximacion_opciones(pseudoskel0_1, quater_sal, _ pseudoskel_incog, 1, 1)
cuaternion_estimacion_total = cuaternion_estimacion_total * quater_sal
distas0 = distas
'gira la primera sobre la segunda
distas = 1000 * distancia_pseudoskel(pseudoskel0_1, pseudoskel_incog)
veces = veces + 1
'retoco angulillo? si sobrepaso minimo
If distas >= distas0 Then
'peligroso
angulo_salto = angulo_salto / 2
If angulo_salto >= salto_incremental Then GoTo otro_angulo
Exit While
End If
End While
dif_cuater = Quaternion.Subtract(cuaternion_estimacion_total, cuaternion_incognita)
Call informar(matriz_ventana.TextBox10.Text + crlf + crlf + _
"Resultados: Cota_distan:" + Str(cota_distan) + "ángulo salto:" + Str(angulo_salto) + _
"salto increm:" + Str(salto_incremental) + "ruido:" + Str(0) + crlf + crlf _
+ "Pasos:" + Str(veces) + crlf _
+ "Incog eje:" + cuaternion_incognita.Axis.ToString() + crlf + _
"Estim eje:" + cuaternion_estimacion_total.Axis.ToString() + crlf _
+ "Incog angle:" + cuaternion_incognita.Angle.ToString() + crlf _
+ "Estim angle:" + cuaternion_incognita.Angle.ToString() + crlf)
' _
' + dif_quater.Axis.ToString() + dif_quater.Angle.ToString + crlf)
Return distas
End Function
____________________________________________________________________________________________Con las dos rutinas auxiliares
____________________________________________________________________________________________Public Sub inicializa_quat_incre(salto_incremental)
Dim quater As Quaternion
Dim mat As Matrix3D
mat = contruye_mat_giro(salto_incremental, 0) : CuaterIncre1 = quat_de_matriz(mat)
mat = contruye_mat_giro(salto_incremental, 1) : CuaterIncre2 = quat_de_matriz(mat)
mat = contruye_mat_giro(salto_incremental, 2) : CuaterIncre3 = quat_de_matriz(mat)
' Case 23 ' <‒-
quater = CuaterIncre1 : quater.Invert() : quater_grad(1) = quater
' Case 25 ' ‒-> = Key.Right
quater = CuaterIncre1 : quater_grad(2) = quater
' Case 26 ' v
quater = CuaterIncre2 : quater.Invert() : quater_grad(3) = quater
' Case 24 ' ^
quater = CuaterIncre2 : quater_grad(4) = quater
' Case 20 'PgDn
quater = CuaterIncre3 : quater.Invert() : quater_grad(5) = quater
' Case 19 'PgUp
quater = CuaterIncre3 : quater_grad(6) = quater
'ver en pantalla
flechas_ver(1) = "←" + " -Y"
flechas_ver(2) = "→" + " +Y"
flechas_ver(3) = "↓" + " -Z"
flechas_ver(4) = "↑" + " +Z"
flechas_ver(5) = "┌" + " -X"
flechas_ver(6) = "┐" + " +X"
End Sub
Public Sub inicializa_quat_salto(angulo_salto)
MatrizBusqueda1 = contruye_mat_giro(angulo_salto, 0) : CuaterBusca1 = quat_de_matriz(MatrizBusqueda1)
MatrizBusqueda2 = contruye_mat_giro(angulo_salto, 1) : CuaterBusca2 = quat_de_matriz(MatrizBusqueda2)
MatrizBusqueda3 = contruye_mat_giro(angulo_salto, 2) : CuaterBusca3 = quat_de_matriz(MatrizBusqueda3)
Dim quater_sal As Quaternion
' Case 23 ' <‒-
quater_sal = CuaterBusca1 : quater_sal.Invert() : quater_salto(1) = quater_sal
' Case 25 ' ‒-> = Key.Right
quater_sal = CuaterBusca1 : quater_salto(2) = quater_sal
' Case 26 ' v
quater_sal = CuaterBusca2 : quater_sal.Invert() : quater_salto(3) = quater_sal
' Case 24 ' ^
quater_sal = CuaterBusca2 : quater_salto(4) = quater_sal
' Case 20 'PgDn
quater_sal = CuaterBusca3 : quater_sal.Invert() : quater_salto(5) = quater_sal
' Case 19 'PgUp
quater_sal = CuaterBusca3 : quater_salto(6) = quater_sal
'Public quater_salto(6) As Quaternion
End Sub
Vea ahora Proyecto Danzante. Reunir imagenes. Aproximacion por micropasos V.Ruido II. ____________________________________________________________________________________________ Nos preguntábamos ¿qué nos queda? 1. Esqueletos completos 2, Variar la distancia, es decir su tipo. (incluso distancias entre cuaterniones y matrices) 3. Añadir orígenes diferentes a cada imagen (translación diferente para cada uno, situación que se presenta con dos cámaras. 4. Operar con dos cámaras reales, diferentes y simultáneas. 5. Promediar los operadores estimados sobre varios esqueletos (¿1 segundo, 30 imágenes?).