Esta página está en construcción: perdonen los errores, repeticiones y temas inacabados.
 
This page is being developed: I am sorry for errors, duplications  and unfinished subjects.
 
 
Proyecto Danzante. Mov XIII. Ordenar caras por distancias al ojo (incluido en Danzante)
 
Este`prob   El problema de la Vision con Tapado entre Objetos
 
y
Objetos virtuales con las propiedades de los objetos humanos
 
 
Orden inverso de dibujo de de icosaedro
= T  1 orden: 15  703 mm
= T  2 orden: 13  760 mm
= T  3 orden: 07  760 mm
= T  4 orden: 20  816 mm
= T  5 orden: 02  852 mm
= T  6 orden: 05  852 mm
= T  7 orden: 08  908 mm
= T  8 orden: 14  908 mm
= T  9 orden: 19  943 mm
= T 10 orden: 17  943 mm
= T 11 orden: 04 1057 mm
= T 12 orden: 01 1057 mm
= T 13 orden: 06 1092 mm
= T 14 orden: 11 1092 mm
= T 15 orden: 16 1148 mm
= T 16 orden: 18 1148 mm
= T 17 orden: 03 1184 mm
= T 18 orden: 10 1240 mm
= T 19 orden: 12 1240 mm
= T 20 orden: 09 1297 mm
   
 
 
 
 
 
lema, qu ela naturaleza reseulce con elgante precision resulta difícil en la simulacion de ese mundo natural.
 
Cuabdo un objeto tapa a otro en el espacio visto por un ojo, el objeto no transparente , opaco, impide ver al ojo, de modo que el punto más cercano de cada rayo de vision oculta a los demás en ese rayo. Si retirams ese ojjeo primero, es el segundo quien tapa a asus posteriores, Y esto para cada rayo de vision. Y esto para cada ojo, quien ordena al mundo que ve de acuerdo a su haz de rayos.
 
Todo esata complicadqa estrategia ha de ser calculada en la sumulacio, resolviendo para cada Ojovietual sus propios rayos de vision, qie son infinitos. Relacionados con esos ojos y sus rayos estna los problemas de la perspectiva, el citado del tapado y el de la colision y interpenetracion de esos objetos, y sobre todo la propia definicion de:
 
Objeto es el espacio (porque hasta ahota sólo manejamps pares de conjuntos. el de Puntos y el de Ramas (o artsyas). Es primera la custiosn de decidir de un parétro o limite externo del objeto, el de Interior o exterioos a ese Límite.
 
 
 
 
 
 
 
emos visto en Planos en el espacio y puntos en ellos los procedimientos para encontrar las caras de iun poliedro. apliquémoslo al icosaedro.
 
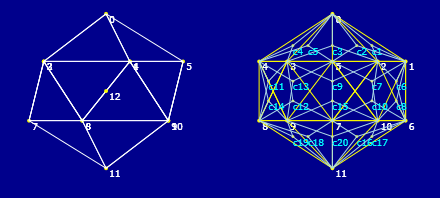icosaedro

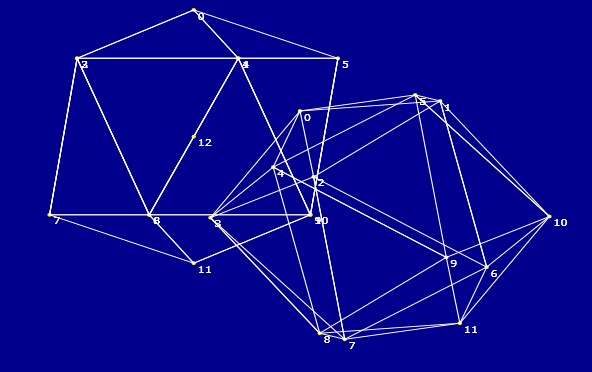1 : _ 0 _ 2 _ 1 _ 6 _ 2 _ 7 _ 6 _ 11
2 : _ 0 _ 3 _ 2 _ 7 _ 3 _ 8 _ 7 _ 11
3 : _ 0 _ 4 _ 3 _ 8 _ 4 _ 9 _ 8 _ 11
4 : _ 0 _ 5 _ 4 _ 9 _ 5 _ 10 _ 9 _ 11
5 : _ 0 _ 1 _ 5 _ 10 _ 1 _ 6 _ 10 _ 11


icosaedro

 

Matriz_conexiones
i j: 0 1 2 3 4 5 6 7 8 9 10 11
0  : - + + + + + - - - - -  -
1  : + - + - - + + - - - +  -
2  : + + - + - - + + - - -  -
3  : + - + - + - - + + - -  -
4  : + - - + - + - - + + -  -
5  : + + - - + - - - - + +  -
6  : - + + - - - - + - - +  +
7  : - - + + - - + - + - -  +
8  : - - - + + - - + - + -  +
9  : - - - - + + - - + - +  +
10 : - + - - - + + - - + -  +
11 : - - - - - - + + + + +  -
 

 T 1: 0 1 2
T 2: 0 2 3
T 3: 0 3 4
T 4: 0 4 5
T 5: 0 5 1
T 6: 1 0 2
T 7: 1 2 5
T 8: 1 5 6
T 9: 1 6 10
T 10: 1 10 0
T 11: 2 0 1
T 12: 2 1 3
T 13: 2 3 6
T 14: 2 6 7
T 15: 2 7 0
T 16: 3 0 2
T 17: 3 2 4
T 18: 3 4 7
T 19: 3 7 8
T 20: 3 8 0
T 21: 4 0 3
T 22: 4 3 5
T 23: 4 5 8
T 24: 4 8 9
T 25: 4 9 0
T 26: 5 0 1
T 27: 5 1 4
T 28: 5 4 9
T 29: 5 9 10
T 30: 5 10 0		 T 31: 6 1 2
T 32: 6 2 7
T 33: 6 7 10
T 34: 6 10 11
T 35: 6 11 1
T 36: 7 2 3
T 37: 7 3 6
T 38: 7 6 8
T 39: 7 8 11
T 40: 7 11 2
T 41: 8 3 4
T 42: 8 4 7
T 43: 8 7 9
T 44: 8 9 11
T 45: 8 11 3
T 46: 9 4 5
T 47: 9 5 8
T 48: 9 8 10
T 49: 9 10 11
T 50: 9 11 4
T 51: 10 1 5
T 52: 10 5 6
T 53: 10 6 9
T 54: 10 9 11
T 55: 10 11 1
T 56: 11 6 7
T 57: 11 7 8
T 58: 11 8 9
T 59: 11 9 10
T 60: 11 10 6
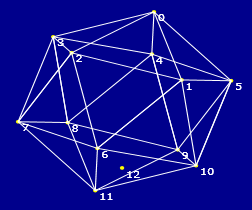T 31: 6 1 2
T 32: 6 2 7
T 33: 6 7 10
T 34: 6 10 11
T 35: 6 11 1		 No están bien, solo los del vertice 0
 
Encontramos todos los triángulos (sin buscar polígonos más grandes (n > 3) que concurren en cada vértice. Naturalmente su número es 60, 3 veces más que el numero de triángulos en el icosaedro que sabemos es 20. Otra vez está claro que en cada vértice concurren varios, 3;  por ejemplo los triángulos 1, 6 y 11 son el mismo, aunque empezando a contar  sucesivamente por cada uno de los vértices.

Se trata ahora de hallar los triángulos equivalentes entre si. Calculemos distancias
 
Matriz_distancias

i j : 00 01 02 03 04 05 06  07  08  09  10  11
00 : --- 70 70 70 70 70 --- --- --- --- --- ---
01 : 70 --- 70 --- --- 70 71 --- --- --- 71 ---
02 : 70 70 --- 70 --- --- 71 71 --- --- --- ---
03 : 70 --- 70 --- 70 --- --- 71 71 --- --- ---
04 : 70 --- --- 70 --- 70 --- --- 71 71 --- ---
05 : 70 70 --- --- 70 --- --- --- --- 71 71 ---
06 : --- 71 71 --- --- --- --- 70 --- --- 70 70
07 : --- --- 71 71 --- --- 70 --- 70 --- --- 70
08 : --- --- --- 71 71 --- --- 70 --- 70 --- 70
09 : --- --- --- --- 71 71 --- --- 70 --- 70 70
10 : --- 71 --- --- --- 71 70 --- --- 70 --- 70
11 : --- --- --- --- --- --- 70 70 70 70 70 ---

 
 		 T 1: 0 1 2
T 2: 0 2 3
T 3: 0 3 4
T 4: 0 4 5
T 5: 1 0 2
T 6: 1 2 6
T 7: 1 6 10
T 8: 2 0 1
T 9: 2 1 6
T 10: 2 6 7
T 11: 3 0 2
T 12: 3 2 7
T 13: 3 7 8
T 14: 4 0 3
T 15: 4 3 8
T 16: 4 8 9
T 17: 5 0 1
T 18: 5 1 10
T 19: 6 1 2		 T 20: 6 2 7
T 21: 6 7 11
T 22: 7 2 3
T 23: 7 3 8
T 24: 7 8 11
T 25: 8 3 4
T 26: 8 4 9
T 27: 8 9 11
T 28: 9 4 5
T 29: 9 5 10
T 30: 9 10 11
T 31: 10 1 5
T 32: 10 5 9
T 33: 10 9 11
T 34: 11 6 7
T 35: 11 7 8
T 36: 11 8 9
T 37: 11 9 10
T 38: 11 10 6
     

Pero ordenando indices de verticw y suprimiento los repetidos encontramos por fin los 20 únicos:

 
T 1: 0 1 2
T 2: 0 2 3
T 3: 0 3 4
T 4: 0 4 5
T 5: 1 0 2
T 6: 1 2 6
T 7: 1 6 10
T 8: 2 0 1
T 9: 2 1 6
T 10: 2 6 7
T 11: 3 0 2
T 12: 3 2 7
T 13: 3 7 8
T 14: 4 0 3
T 15: 4 3 8
T 16: 4 8 9
T 17: 5 0 1
T 18: 5 1 10
T 19: 6 1 2
T 20: 6 2 7
T 21: 6 7 11
T 22: 7 2 3
T 23: 7 3 8
T 24: 7 8 11
T 25: 8 3 4
T 26: 8 4 9
T 27: 8 9 11
T 28: 9 4 5
T 29: 9 5 10
T 30: 9 10 11
T 31: 10 1 5
T 32: 10 5 9
T 33: 10 9 11
T 34: 11 6 7
T 35: 11 7 8
T 36: 11 8 9
T 37: 11 9 10
T 38: 11 10 6
 		 encontramos y marcamos los repetidos:

T 1: 0 1 2
T 2: 0 2 3
T 3: 0 3 4
T 4: 0 4 5
T 5: 1 0 2= T 1
T 5: 1 2 6
T 6: 1 6 10
T 7: 2 0 1= T 1
T 7: 2 1 6= T 5
T 7: 2 6 7
T 8: 3 0 2= T 2
T 8: 3 2 7
T 9: 3 7 8
T 10: 4 0 3= T 3
T 10: 4 3 8
T 11: 4 8 9
T 12: 5 0 1
T 13: 5 1 10
T 14: 6 1 2= T 5
T 14: 6 2 7= T 7
T 14: 6 7 11
T 15: 7 2 3= T 8
T 15: 7 3 8= T 9
T 15: 7 8 11
T 16: 8 3 4= T 10
T 16: 8 4 9= T 11
T 16: 8 9 11
T 17: 9 4 5
T 18: 9 5 10
T 19: 9 10 11
T 20: 10 1 5= T 13
T 20: 10 5 9= T 18
T 20: 10 9 11= T 19
T 20: 11 6 7= T 14
T 20: 11 7 8= T 15
T 20: 11 8 9= T 16
T 20: 11 9 10= T 19
T 20: 11 10 6
 
Triángulos diferentes encontrados
 
T 1: 0 1 2
T 2: 0 2 3
T 3: 0 3 4
T 4: 0 4 5
T 5: 1 2 6
T 6: 1 6 10
T 7: 2 6 7
T 8: 2 3 7
T 9: 3 7 8
T 10: 3 4 8
T 11: 4 8 9
T 12: 0 1 5
T 13: 1 5 10
T 14: 6 7 11
T 15: 7 8 11
T 16: 8 9 11
T 17: 4 5 9
T 18: 5 9 10
T 19: 9 10 11
T 20: 6 10 11




 
 
 
 

Hasta ahora encontramos sólo los triángulos.
 
 
 
Vuelta al Principio    Última actualización: martes, 27 de septiembre de 2016    Visitantes:contador de visitas