Esta página está en construcción: perdonen
los errores, repeticiones y temas inacabados.
This page is being developed: I am sorry for
errors, duplications and unfinished subjects.
Distancias entre esqueletos IV.
Función
a minimizar
(incluido en
Danzante)
Las funciones distancias
introducidas en
Distancias entre esqueletos.htm y
I y comentadas en
II, se comportan
muy bien en la búsqueda de mínimos. Sobre una superficie esférica,
el arco de círculo máximo y su cuerda disminuyen monótonamente al
acercarse dos puntos por ese círculo que es el más corto entre los
posibles (otra cosa ocurre en esferas no perfectas, como la Tierra,
con sus loxodromias). Algún círculo máximo no oscila, si su eje pasa
por el punto destino. Si el círculo no es máximo, caso más
frecuente, sigue habiendo una ondulación pero varía menos, teniendo
una media no nula como línea de base.
Además arco y cuerda llegan
a 0 y luego comienzan a crecer al sobrepasarlo. Si el círculo máximo
no pasa por ambos puntos, entonces no obstante la distancia
disminuye también monótonamente, pasando por un mínimo no nulo y
luego creciendo. Estos círculos, 3 de ellos perpendiculares
(circularmente perpendiculares) son los que corresponden a los giros
que usamos para acercar dos p_esqueletos en la estrategia de los microsaltos (ver
Aproximación por micropasos III y anteriores).
Sobre la esfera en que nos movemos,
esas distancias tienen también un máximo (igual al diámetro si el
circulo máximo para por ambos puntos)., de modo que los movimiento
continuados sobre los tres círculos citados ocasionan tres
movimientos harmónicos o al menos ondulados.
Así que los giros elementales
corresponden a buscar una función de tres variables con incrementos
en cada una. Es un campo escalar, en suma, del
cual hallamos el gradiente en cada punto.
Ahora bien la media de las
distancias de cada articulación será una media de las ondulaciones
citadas. Su frecuencia es la misma, variando sólo su fase, su
amplitud y distancia y elongación media. Su suma, por lo tanto es una
ondulación de
igual frecuencia. En cuanto a la ecuación concreta de cada
una, obtenemos, tras algo de trigonometría, para cada una de
las articulaciones:
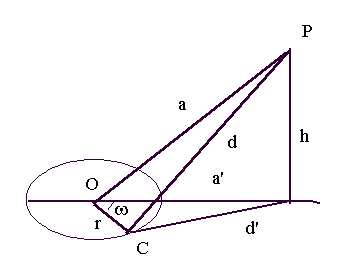
d 2 = a' 2 + r 2 + h 2
+ 2 r a' cos(w)
siendo d
la distancia del punto P al punto del C del círculo, a
la distancia de P al centro del círculo O,
r,
el radio de éste y w
el ángulo del radio de C con a',
proyección de a sobre
el plano del círculo (después la llamamos b)
que es la distancia en el plano entre el centro del círculo y la
proyección de P sobre le plano, y h
la distancia de P al plano del círculo.
Para todo el esqueleto {e i
}, tenemos, llamando b
a a'
D2 = S i { d
i 2 } = S i
{ b i 2 + r 2 + 2 r b i
cos(w+ f i
) }
expresión cuadrática cuyo mínimo buscamos variando la
orientación del plano del círculo (giramos el plano o el conjunto de
puntos {e i
}).
Cada sumando es una oscilación con
máximos de valor ( b + r ) 2 + h 2, mínimos de valor (
b - r ) 2 + h 2, y recta media de valor b 2 + r 2 + h 2,
pero desfasados constantemente (durante la variación de
w) ángulos
f i dependientes
de su posición relativa respecto a la articulación de referencia
(generalmente la 2), invariable durante el giro. Pero esa suma se
reduce en definitiva a constantes más cosenos de igual frecuencia
w y fase diferente.
Como la suma de esos cosenos desfasados es otro coseno de la misma
frecuencia y fase f i
dependiente de fase
f i
dependiente de todas
las fase f i
y los coeficientes de
esos cosenos * tenemos simplemente que hallar el mínimo de una
función coseno multiplicada por una constante más otra constante:
D2 = K1 + K2 cos(w+ f
) }
cuyo mínimo obtenemos derivando
e igualando a 0:
dD2/dw
= - K2 sen(w+ f
) cos(w+ f
) = - (K2 /2) . sen(2w+ 2f
) = 0
cuyas soluciones son claramente dos: w1
= - f
w2 =
- f+p en un entorno de una vuelta (-p
a p ) y sus valores asociados w = - f
+ kp
con k entero (positivo o negativo).
Es decir sobre la esfera tenemos un
sólo mínimo y podemos calcularlo según la expresion anterior. O bien
podemos acercarnos en la direccion de la desuancia decreciente hasta
llegar a una aproximación tan cercana como deseemos, iterando por el
método de Newton (Aproximacion
por micropasos III).
Así podríamos obtener el
ángulo
w
óptimo para cada esqueleto. Pero preferimos comprobarlo
empíricamente en algunos casos, elegidos como presumiblemente
representativos de las posibilidades mil que pueden presentarse.
Vamos a dibujar esta función para comprobar si es monótona (en los
casos ensayados), como creemos, o aparecen mínimos locales que
podrían dificultar la búsqueda del mínimo absoluto. El giro elegido
_____________________________________________________________________
*
dD2/dw =
S i
d {d i 2} /dw =
S i
d
{ b i 2 + r 2 + 2 r b i
cos(w+ f i
) }/dw =
= S i { 2 r b
cos(w+ f i
) sen(w+ f i
) } = S i
{ 2 r b
cos(w+ f i
) sen(w+ f i
) } =
= S i { r b sen (2w+
2f i
) } = 0
o sea, una suma de
senos desfasados de igual frecuencia.
Vuelta al Principio Última
actualización:
jueves, 10 de septiembre de 2015
Visitantes:
