Últimas consideraciones sobre Disonancia Rítmica
Vamos añadiendo las cuestiones que se nos van suscitando sobre la Disonancia Rítmica. He aquí las presentes hasta ahora.
Índice
Escalas rítmicas Disonancia rítmica de un ritmo de duraciones. Diagramas rítmicos Mariposa Golpes aislados y contiguos compases subdivididos Experimentos para determinar correlación entre media de DR y tiempo de aprendizaje Circularidad y Rotación de los Ritmos.
Escalas rítmicas
Tomamos el concepto de su uso tonal. La idea es la misma: cada figura rítmica que sigue a otra establece con ella una sonancia equivalente a la presencia de dos tempos simultáneos. Para ello hace falta un origen común, para que se establezca dos periodos de repetición. En un compás de N partes o figuras (C es cuatro negras) la primera y segunda notas de un compás están es relación respecto al principio del compás anterior:
N : N+1
cuya sonancia común depende obviamente de N: cuanto más complejo, según los caculos objetivos de sonancia que se han ido definiendo antes, más disonante es la combinación.
En un compás de 8 (por ejemplo, 8 corcheas)
|
|
| Compás de 8 por 4 (8 negras) |
| 8:.8 9:8 10:8 11:8 12:8 13:8 14:8 15:8 | 16:8
al momento salta a la vista la similitud de estas razones con las correspondientes a las de los intervalos de la escala mayor natural con la tónica. De ahí el apelativo que hemos elegido, Escalas Rítmicas.
Observamos en particular las razones correspondientes al Tono mayor (9.8), tercera mayor natural, quinta justa y séptima mayor natural.
En realidad esta escala es idéntica a una de las Escalas Regulares, definidas por nosotros hace unos años para el tono, a la ER8 en concreto.
El compás de 12 (por ejemplo, 12 negras)
|
|
| Compás de 12 por 4 (12 negras) |
| 12:12 13:12 14:12 15:12 16:12 17:12 18:12 19:12 20:12 21:12 22:12 23:12 | 24:12
que incluyen los conocidos intervalos Cuarta justa (16:12 equivalentes a 4:3), la Quinta justa (18:12 <>3:2) y la Sexta natural mayor 20:12 <> 5:3),
Pasando a denominador 24 --el cual no escribimos para simplificar la notación-, queda:
| 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 | 48
do re mi fa sol la si do
Para obtener un escala rítmica de razones iguales a la mayor natural (tonal) hay que conseguir razones deferentes para el FA (4:3) y el LA (5:3), aun tono mayor y uno menor respectivamente a cada lado del SOL (3:2 o 12:8 ) que tomamos de la escala de 12.
|
1 2 3
4 5
6 7
| 8
do re mi
fa sol
la- si- |
do
|
| Escala 'mayor natural' Rítmica en 24 partes: Dison.general (p=1.5): 0.330 |
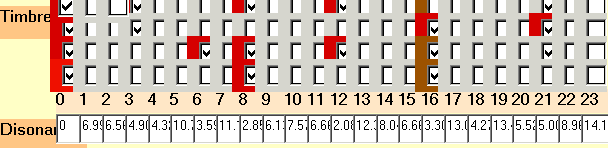 |
| Oiga este ritmo-regular-8 |
Ello se consigue fácilmente pasando a la escala ternaria (de 12) puntualmente, o sea, empleando tresillos. En efecto, la razón 5:4 más 16:12 equivale a 2 negras normales (que representamos con la plica abajo) mas otra perteneciente a un tresillo (que representamos con la plica arriba).
|
1 2
3 4 5
6 7 | 8
do re mi- fa sol la- si- | do
|
| Escala mayor natural Rítmica. Plica arriba son tresillos. (repasar la figura) |
Escúchela. Hemos atribuido timbre grave a Do, Sol y La (¡rítmicos!), y agudo a las demás notas (¡rítmicas!)
Por cierto, la primera parte de ese ritmo casi coincide con el de la clave cubana: se reduce el ritmo a 16 y se intercambian los dos últimos grupos de figuras:
|
|
| La clave cubana, en 16 partes |
¿Serían conscientes los inventores de este ritmo (presumiblemente africano) de las implicaciones numéricas anteriores?.¿Oirían esas relaciones?.
Disonancia rítmica de un ritmo de duraciones.
Se definió como la disonancia común de todos los golpes, es decir, de todos los ciclos de períodos N, número de golpes del compás, y N+ni , siendo ni el intervalo temporal desde cada golpe al principio del compás, medido, claro, en unidades del golpe. Así, siempre N > ni . Se divide después por el número de golpes, intentando obtener el rendimiento rítmico de cada golpe. es decir, si cada golpe acentúa o mitiga la disonancia general.
Diagramas rítmicos de Mariposa
Con las medidas anteriores vamos a trazar las disonancias citadas sobre los radios de un círculo dividido precisamente en N sectores.
Por ejemplo, veamos el gráfico circular de disonancias de dos compases similares, muy vecinos: de 32 y de 16: podemos decir que el primero se obtienen subdividiendo el segundo.
|
|
 |
| Valores de DR para dos compases de 16 y 32 partes. Nótese la coincidencia cada dos valores de la larga con los de la corta. |

Si dibujamos un radio proporcional a la disonancia rítmica de
parámetro 1 (DR1 desde ahora), y hacemos el ángulo de cada punto igual al
circulo dividido por el número de partes, observamos dos gráficos, el
interior, en rojo, pa ra 16 y el exterior, en verde, para 32. El segundo es
exterior y más grande porque contiene golpes muy disonantes, que se reflejan
en gran radio. El comienzo del círculo correspondiente al principio de compás
se elige arriba, y el crecimiento temporal hacia la derecha (el del reloj)
ra 16 y el exterior, en verde, para 32. El segundo es
exterior y más grande porque contiene golpes muy disonantes, que se reflejan
en gran radio. El comienzo del círculo correspondiente al principio de compás
se elige arriba, y el crecimiento temporal hacia la derecha (el del reloj)
Podemos consideran que ambos coinciden en la mitad de los puntos del 32 con todos los puntos de 16, pero 32 añade puntos mas disonantes, que se reflejan como triángulos que crecen hacia afuera con la base de los segmentos del menor, 16.
Observamos que los golpes que preceden a los más consonantes (0 y N/2, en la vertical) son los más disonantes: son las anacrusas, que preparan y exigen irresistiblemente su resolución en aquellos.
Podemos repetir el dibujo para un exponente de la norma (seminorma en concreto) con parámetro fraccionario, de valor p=1.7, lo que modera las diferencias entre radios. Lo hacemos como antes para compases de 32 y 16, el segundo interior al primero. Se observa una correspondencia o parecido entre los dibujos.
Estos gráficos y sus valores corresponden a las medidas de disonancia que hemos definido hasta ahora, es decir, compases sin estructura de partes. Se han obtenido mediante la ventana de RITMOS en Mapatone, versión 5.
Golpes aislados y contiguos
Don golpes contiguos, es decir, ocupando lugares contiguos en el compás, devienen perceptivamente uno sólo: el segundo se añade al primero, que queda simplemente más largo.
De modo que todo calculo de disonancia DR media ha de tener en cuenta ese efecto perceptivo. Por ejemplo, un golpe muy disonante precedido contiguamente por otro que lo es menos, queda atribuido al primero y 'pierde su disonancia en el conjunto.. Para que el efecto disonante de un golpe se manifieste ha de ser único o el primero de una serie.
Así que los cálculos de
DE UN RITMO HAN DE TENER EN CUENTA SÓLO LOS 'PRIMEROS GOLPES', LOS `PRECEDIDOS DE SILENCIO.
Podemos también considerar la influencia del tempo, o sea el intervalo entre unidades del compás. Un tempo rápido funde varios golpes seguidos en un o sólo, uno sólo dotado de un rasgo o cualidad: el redoble, un sonido de percusión continuo, dotado de duración.
Por eso, un compás en el que todos los golpes están seguidos, es un compás poco disonante, es como un compás con un sólo golpe en la primera subparte.
Este acercamiento, no obstante ha de ser referido al tempo: en efecto, un tempo muy lento individualiza cada golpe del contiguo, mientras que uno rápido, lo funde en un redoble o textura rítmica.
Tenemos que introducir el tiempo y el tempo en esta estrategia.
Compases subdivididos
La medidas definidas en Disonancia Rítmica admiten algunas ajustes para valores grandes de N, el número de percusiones posibles, o sea, el número de pulsos del motor o tempo,
Ello es debido a que, en el desarrollo de un ciclo rítmico, vamos discurriendo en el tiempo y los golpes no están referidos en nuestro espíritu (a falta de otro mejor) con referencia al primero del ciclo, sino a mojones parciales, golpes privilegiados, es decir, aquellos que determinan las partes o subpartes de un compás inicial temporal directo.
Por ejemplo, en un compás de compasillo con un motor de corcheas, la tercera se refiere, se siente como 'la siguiente a la primera de la segunda parte. En un compás de 12 por 8, la 6ª es la tercera, la última de la segunda parte (partes son 3 corcheas), o la anterior a la primera de la cuarta, pero no se concibe directamente como la sexta del compás completo. Y más aún si se trata de la 7ª, de muy difícil conexión con la primera del compás, aunque mejor con la primera del siguiente compás, como anacrusa.
Es decir, en la comprensión de un ritmo algo largo, por ejemplo a partir de 5 o 6 impulsos en un compás, casi inevitablemente dividimos el compás en partes, iguales, lo fácil, o desiguales, en los llamados ritmos de adición.
Esa división del compás lo estructura, y es la que debe reflejarse en toda medida de la disonancia rítmica. Es decir, esta medida debe referirse a la división que músico y oyente (experto) realizan sobre el ciclo del compás.
Empezaremos por lo tanto calculando las disonancias de los golpes principales, los primeros de las partes, y después calcularemos los demás con referencia a esos primeros, como lo describimos más arriba. Llamaremos a estas disonancias así calculadas Disonancias Rítmicas Compuestas, DRC, contrastando con las anteriores, DRS, simples.
El problema se transfiere ahora a cómo combinar las disonancias parciales de cada golpe respecto a su subparte principal con las disonancias globales de estos.. Para ello se nos ocurren las siguientes reglas o guías:
1. Las disonancias globales y compuestas han de coincidir para subdivisiones regulares (subpartes iguales).
Experimentos para determinar correlación entre media de DR y tiempo de aprendizaje
Se trata de evaluar si alguna o más de las medidas propuestas para la DR se corresponden bien proporcionalmente, bien mediante una función sencilla (potencial, exponencial, logarítmica...) a la dificultad psicológica.
El tempo es muy importante en ese aprendizaje: cuanto más rápido más sencillo; es como si la consciencia rítmica se extiende a un pequeño intervalo de tiempo, una especie de 'presente' en el que las relaciones de duración son más sencillas de absorber. Ese presente viene a durar 1 segundo, aproximadamente. De modo que el tempo es un parámetro esencial en esa dificultad: o, por el contrario, las mediad subjetivas de complejidad han de tenerlo en cuenta. Pero el tempo ocasionaría --creemos-- un simple cambio de escala, es decir, la curva de correlación, de existir, se conservaría con un simple escalado de una de las variables, traería sólo un cambio, otro, de escala.
El tiempo necesario para aprender un ritmo --aprendizaje que se prueba tocándolo o cantándolo sin errores-- tiene que ver obviamente con la dificultad o complejidad del ritmo. Se trata de saber si las medidas objetivas propuestas recogen o reflejan esa diferencia.
Es de esperar que esas curvas --repetimos, de existir-- sean independientes de la pericia musical del sujeto de experimentación; pericia que, igualmente se manifestaría mediante un cambio --otro-- de escala
Circularidad y Rotación de los Ritmos.
A un determinado patrón rítmico, un ritmo, en principio de duraciones, puede achacársele una sonancia , que depende de las sonancias parciales de sus golpes. En principio la manera más simple es sumar esas sonancias, suma que será tanto mayor cuanto mayores sean los sumandos.
Pero procede calcular la disonancia media, más que la suma. Esto permite referir la dificultad de un ritmo con el número de sus golpes. Cuanto menor sea este número y mayor la DR de sus golpes, mayor será esta DR media. Añadir golpes sencillos disminuye la dificultad y suprimirlos la aumenta. E introducir golpes complejos (alta DR) aumenta la DR media mientras que suprimirlos simplifica el ritmo. Todo esto está acorde con la experiencia rítmica, la experiencia de la dificultad o facilidad de un ritmo a la que aludíamos en el párrafo anterior.
Por ejemplo el ritmo regular 8, antes estudiado y representado no cambia su ordenación al circularlo: su disonancia es mínima así, lo que debe tener que ver con su naturaleza de 'ritmo harmónico', o sea, compuesto por golpes harmónicos
Vuelta al Principio Última
actualización:
viernes, 25 de julio de 2014 Visitantes: