Esta página está en construcción: perdonen los errores, repeticiones y temas inacabados.
This page is being developed: I am sorry for errors, duplications and unfinished subjects.
Entrelazados (perteneciente a Decoración Geométrica Islámica)
C + V = A +`2
Funciona con curvas, con sólidos o con planos (admitiendo exterior de figura como una cara).
Cada nueva varilla añade cuatro en forma de cuadrilatero o en forma de variacion de existente más una nueva
En el estudio de las Riges (redes islámicas geométrica entrelazada) es esencial revisar los movimientos o transformaciones geométricas en el plano, porque este tipo de decoración hace uso extensivo de ellas. ¿Por qué?. Porque el ojo y la percepción agradecen gustan de ellas al reconocer los parecidos entre partes de la figura total.
las transformaciones recogidas por la geometría tradicional son:
Translaciones o desplazamientos. Giros Simetrías axiales Simetrías centrales Homotecias Inversiones
De ellas son más importantes y o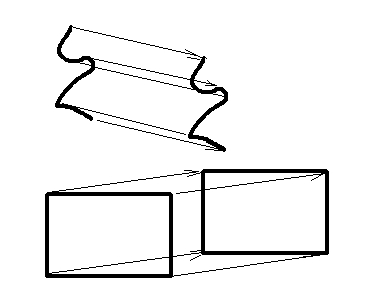
bvias las tres primeras, menos evidentes pero
importantes la cuarta; la quinta no sabemos que aparezca, pero quizá valga la
pena examinar el caso. veámoslas:
Translaciones o desplazamientos
Una figura sufre o experimenta una translación cuando todos sus puntos lo hacen igualmente, es decir, cuando todos los segmentos que unen un punto y su trasladado son paralelos y de igual longitud. Estos segmentos quedan representados por uno de ellos, con sentido del origen al destino, o sea, un vector.
Para trasladar una figura compuesta de segmentos rectos, de una o varias líneas poligonales, basta trasladar los vértices y unir después sus trasladados, lo que reconstruye la figura original en su nueva situación.
Simetrías axiales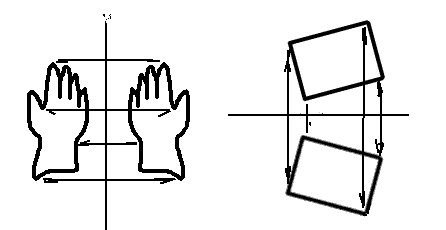
Es la simetría por excelencia, la que hace corresponder las dos manos, un objeto y su reflejo en el espejo, etc. Como dice su nombre presupone un eje, el eje de simetría, que es un recta tal que todo segmento que une un punto y su simétrico es perpendicular al eje y es cortado por él en el centro. También podemos decir que las distancias (perpendiculares, claro) de los puntos simétricos al eje son iguales (y sobre la misma recta).
En la figura vemos dos imágenes de formas simétricas, con ejes respectivos vertical y horizontal.
Simetrías centrales y giros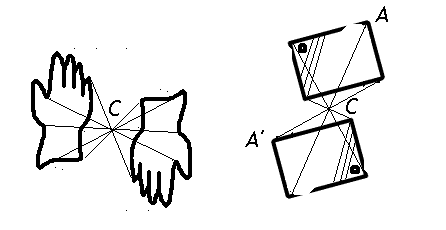
En este caso tenemos un centro de simetría, C en la figura que es un punto, por cual pasan todos los segmentos que unen puntos homólogos. Y, como antes, el centro de simetría divide en dos esos segmentos.
El ojo considera este movimiento como un giro alrededor de C, un giro de 180º. Veamos otros giros.
Giros
El giro es un movimiento similar a la simetría central, pero ampliando el
giro en ella que es de 180º a cualquier ángulo. Son especialmente int
eresantes
lo giros que podemos llamar regulares, es decir aquellos que tras repetirse
varias veces vuelven al punto de partida. Son evidentemente giros de ángulo
divisor entero de una circunferencia.
Homotecias
En este caso hay un centro también, pero la relación entre segmentos que unen en centro con los puntos homólogos ya no son iguales en general, sino que guardan una proporción, la misma para todos los pares. Esto quiere decir que las figuras homotéticas tienen la misma forma pero tamaños diferentes, como ocurre con un objeto visto de cerca y de lejos.
Podemos definir la razón de homotecia k como la ra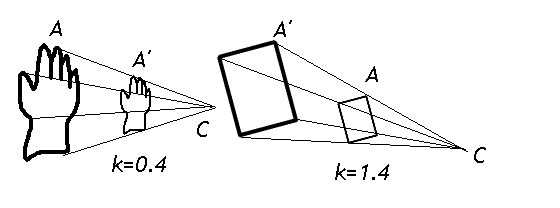
zón
(cociente) entre las
longitudes del segmento que une un punto con el centro de homotecia y la del
segmento que une su homólogo o homotético con el centro. En la segunda figura es
k = A' C / AC
Inversiones
La inversión involucra una circunferencia y la dejamos por ahora.
Combinaciones de varios movimientos
Pétalos
Combinando simetrías axiales y giros regulares se producen una serie circular de formas radiales simétricas respecto a su eje central: son como pétalos, y aparecen con mucha frecuencia en esta decoración, quizá porque recuerda a una flor.
Espacio de movimientos
Exceptuando por el momento la inversión, el conjunto de movimientos definido forma un conjunto dotado con una estructura que nos parece de espacio vectorial: vamos a comprobarlo
Que la composición (o suma) de movimientos es otro movimiento, resulta fácil probarlo.
| Trans. | Sim.Ax. | Sim.Cent. | Giro | Homo. | |
| Trans.. | T | ||||
| Sim.Ax. | |||||
| Sim.Cent. | |||||
| Giro | |||||
| Homo. |
Demostremos que:
Dos figuras iguales en el plano son superponibles mediante un sólo giro.
para ello no tenemos mas que demostrar que, con el mismo centro, toda pareja de puntos homólogos presenta el mismo ángulo. Esto de consigue trazando la perpendicular media a los segmentos que unen cada pareja homóloga.
Simetrías y la red
Un eje de simetría en una red lo es si todo elemento de la red y su simétrico perteneces a esa red. Puntos, rectas polígonos pueden encontrar su simétrico respecto a uno o varios ejes.