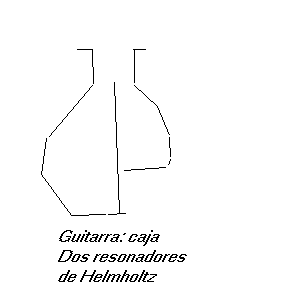
6. Aire y Caja (incluido en Acústica de un instrumento de cuerda)
Hay opiniones encontradas, a veces violentamente, sobre si el aire de la caja de resonancia 'suena' o no.
El sonar consistiría en que ese aire, como ocurre en un tubo, vibra una vez independientemente del sistema excitador (cuerda-puente-tapas), como ocurre en un tubo sonoro. No es igual decir 'tuuu' por un tubo y que se oiga por el otro extremo, que excitarlo como una flauta y que emita un sonido que podemos llamar propio. En el primer caso, el tubo es un mero transmisor del sonido. En el segundo es también un emisor. Este es el punto central, creemos, a considerar.
¿Vibra el aire de la caja emitiendo un sonido?. Lo hará si, y solo sí, se excitan (mediante las tapas) sus frecuencias propias como volumen que es (recuérdense la ocarina, los resonadores de Helmholtz, las botellas, los propios tubos sonoros de órgano, etc.).
Leemos en Olson (1962-67, pag.72) que la frecuencia fundamental de un resonador de Helmholtz, es decir, una cavidad con un agujero (el otro presente se aplica al oído y queda cerrado, no repercute en el sonido) es:
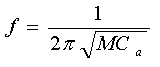
donde M es la inertancia del agujero en gr/cm4 es, para un agujero circular de radio R, siendo r la densidad del aire en gr/cm3, y l el grosor de la pared del agujero en cm:
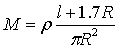
si el orificio no es circular, puede adoptarse la aproximación.
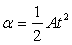
y Ca=capacitancia acústica cm/dyna que vale
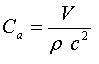
lo que, sustituyendo, nos lleva a:
.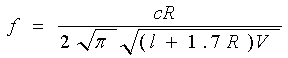
Para agujeros no circulares se ofrece la fórmula alternativa de M en función del área A del orificio. Fundiendo ambas fórmular en una queda:
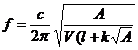
en la que la constante k vale, según su forma (o simplemente según la fórmula)
1 < k < 1.041 (que proporciona 1.77, valor para orificio circular).
Es decir, recapitulando, la frecuencia resonante sube al aumentar el agujero y/o disminuir el volumen, y baja consecuentemente. El agujero o boca no sólo sirve para que salga el sonido, tiene una función en el timbre general. En ese sentido serían equivalentes pequeños volumen y boca o grandes ambos (por ejemplo, aumentando el volumen al cuádruplo, caja 1.6 veces mayor en todas sus dimensiones, y el radio del agujero al cuádruplo [2=x/raiz(x); x=4]; luego aumenta R mucho más proporcionalmente); si no fuera porque la potencia acústica de la amplificación variará también, será menor para caja pequeña, y además hay límites para esa boca que aumenta más rápidamente que el volumen o que disminuye hasta hacerse casi nula. Como en todo hay un compromiso, empíricamente encontrado por los luthiers expertos, probando y probando.
Ejemplo: Empíricamente oímos un RE de 146 hz al excitar el aire de una caja de guitarra portuguesa (la de los fados), matando la vibración de las cuerdas. Medimos someramente las dimensiones de la caja:
Superficie: (18+15) / 2 = 16.5 * 6.28 cm2
Profundidad interior: (9.5+6.5) / 2 = 8 cm Volumen = 16.5 * 8 *6.28 = 8 litros aprox. R=4cm, l despreciable,
Hechas las cuentas nos salen: 163.9 hz, no muy alejado de los 146 medidos, dada la imprecisión de las medidas. (compruébese que las dimensiones en la fórmula son T-1)
Comprobamos además que cuando una cuerda da esa nota, resuena más que las vecinas: problema: este instrumente toca en re pero en do# o mib.
También comprobamos que tapando la mitad del agujero (boca en término guitarrero, o tarraja) el sonido baja a 120 hz, confirmando la importancia de esa boca en la nota lobo: primera consecuencia: si queremos desplazar la frecuencia de la nota .lobo, modificamos el diámetro de esa boca. O el grosor, que también influye algo.
Tomamos una bandurria de concierto modelo calvete; curiosamente la nota-lobo es casi igual que para la guitarra portuguesa, 148 hz. aunque el instrumento es mas pequeño, la distancia entre tapas es mayor (más volumen) y el agujero o boca más pequeño: se llega casi a lo mismo.
Una guitarra, da unos 100 hz, un sol. También resuena con la octava.
| INSTRUMENTO de CUERDA | ||
| Resonancia del aire interior de la caja | ||
| Instrumento | Hz | Nota-Octava |
| Guitarra portuguesa (tipo bandurria grande) | 146 | Re 4 |
| Bandurria | 148 | Re 4 |
| Violín | 262 | Do 5 |
| Guitarra | 100 | Sol 3 |
En todos los casos, la nota está dentro de la tesitura del instrumento con su doble posibilidad de actuar como formante beneficioso en una zona de frecuencias no cubierta por las tapas. Como perturbación que crea picos de frecuencia en zonas de la escala. Es decir, parecería que es bueno u formante ancho y malo uno estrecho
Pero no solo importa la frecuencia de resonancia sino también la extensión de la zona que rodea a esa frecuencia compuesta de otras frecuencias que también son algo resonantes. Es decir la resonancia tiene una forma de montaña mas o menos amplia y esa anchura es medida por una variable o parámetro llamada Q depende de las dimensiones relativas del volumen y diámetro del agujero. Su expresión es:
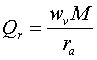
donde ra representa la resistencia acústica y vale:
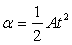
sustituyendo:
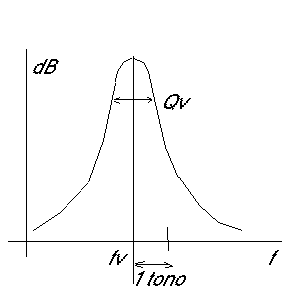 |
| Efecto de Q en las frecuencias vecinas a la de resonancia |
¡Cual es el efecto de esta Q. La curva de la figura muestra cómo reacciona el aire de la cavidad ante una frecuencia f: resuena o no. Resuena siempre para fv y peor para frecuencias vecinas. Cuanto peor?. Si Q es ancho, grande, poco peor, casi resuena igual. Si Q es pequeño, mucho peor: sólo resuena para fv prácticamente: es un resonador muy refinado, muy selectivo como los de Helmholtz.: Mucho volumen y poco agujero: y esto es lo vemos en la fórmula anterior.
De esta fórmula ya se deducen muy interesantes propiedades:
La anchura de la resonancia es mayor para boca o agujero de la caja (las efes o eses del violín)
Veamos si podemos entender los conocimientos ancestrales de los luthiers expertos:
Un violín en nuestro poder resuena en un DO, aunque Backus (1977, pg.200) dice que debe ser un RE
Otro instrumento, una guitarra, resuena a FA-6-1 (6º cuerda, primer traste); pero también a un LAb-3-3. Hay dos resonancias: quizá correspondientes a las dos anchuras de la caja?. Quizá porque esos volúmenes pueden ser uno doble del otro, lo que ocasiona una relación de raíz de dos en las resonancias, 1.4, una cuarta aumentada, no muy diferente del a octava+mas la tercera menor encontrada. Otra guitarra, da lab o sol# 6-4 y fa# 4-4
Intervalos de amabas resonancias: 10º y 7º. Se dice que Torres buscaba una intervalo con sus medidas ¿sería con estas resonancias?
|
|
|
|
Unos datos empíricos: si el volumen de la caja es demasiado grande suena como un caldero, es decir, pierde brillantez, el sonido ya no es agudo, destacado.
Por parte del agujero, al agrandarlo demasiado, también se diluye el sonido, no tiene empaque.
¿Como unir el empaque con el Q?
Resulta que este Q también representa, mide el tiempo de amortiguación de un sonido impulsivo, que se desea largo. Como Q es también un filtro pasa-banda en las bajas frecuencias, acentúa la baja frecuencia cuya variación en el tiempo es lenta. Un impulso de excitación quedará suavizado en timbre y acentuadas sus bajas frecuencias: un larga cola de atenuación.
También se llama a Q rozamiento interno: energía disipada frente a la almacenada elásticamente. Y también se le llama factor de calidad.
Este Q no sólo se estudia en relación con el aire sino también a cada uno de los modos propios de vibración de las tapas y de todo.
Es decir la respuesta general del instrumento a las excitaciones de la cuerda se compone de la acción combinada, suma, de las respuestas de cada formante asociado a cada modo de vibración, bien de las tapas, bien del aire /el más bajo según Backus) bien de cualquier otro origen. Si el primer modo de vibración de la tapa superior cubre de de RE a SOl, y el segundo del fondo, de SOL a DIO, y el aire de DO a MI, entre todos amplifican todas las frecuencias en esa tesitura. A priori se piensa que una respuesta plana es la mejor. P3ero a lo mejor un cierto grado de color es necesario para la calidad. La respuesta plana corresponde más bien a la eficiencia del sistema acústico del instrumento, que amplifica bien todas las frecuencias de las cuerdas.
 |
Y la nota-lobo: esto es otra historia
Vuelta al Principio Última
actualización: Thursday, 21 de February de 2013
Visitantes: