Esta página está en construcción: perdonen los errores, repeticiones y temas inacabados.

This page is being developed: I am sorry for errors, duplications  and unfinished subjects.

Proyecto Danzante.   Problemas de saltos en la serie optimizada  (incluido en Danzante)

 

Nos referimos a saltos en la película del esqueleto optimizado, que hace una morisqueta de vez en cuando, sin que las sufran los dos cooperantes (p y q). hemos notado ese salto al reproducir la película del los cuatro p_esqueletos intervinientes, 0, 1, 2,  3, que son:

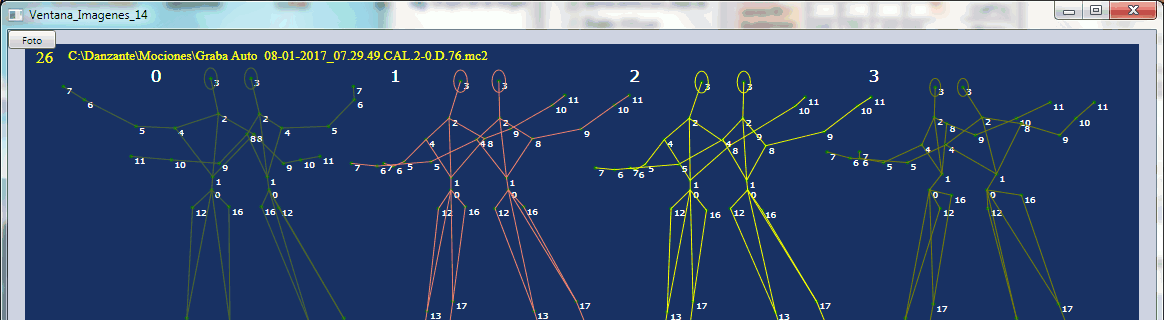
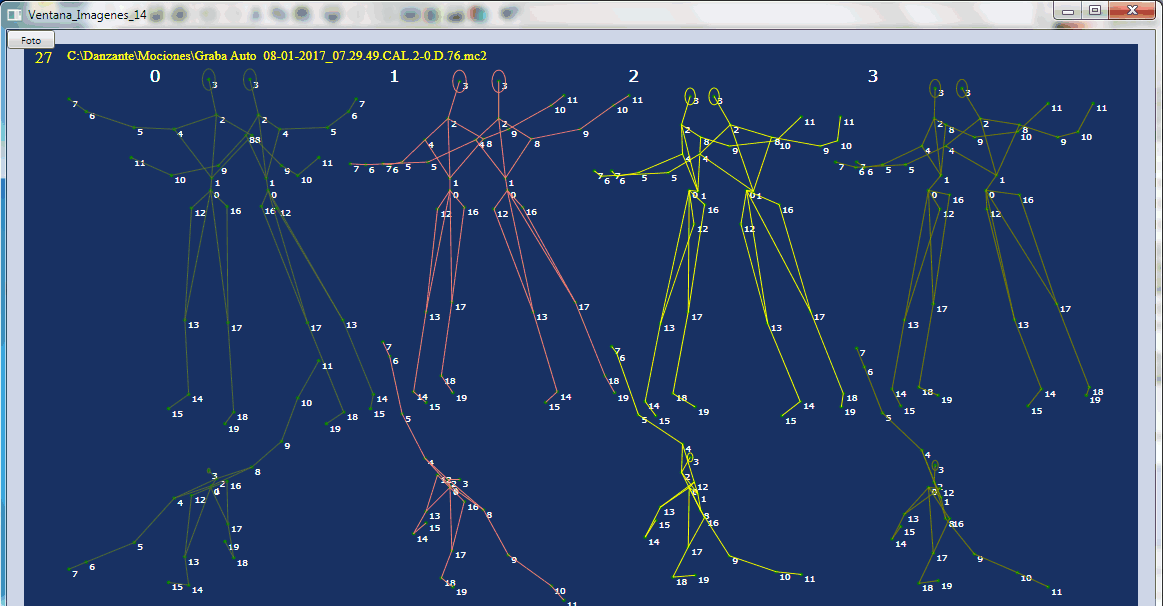
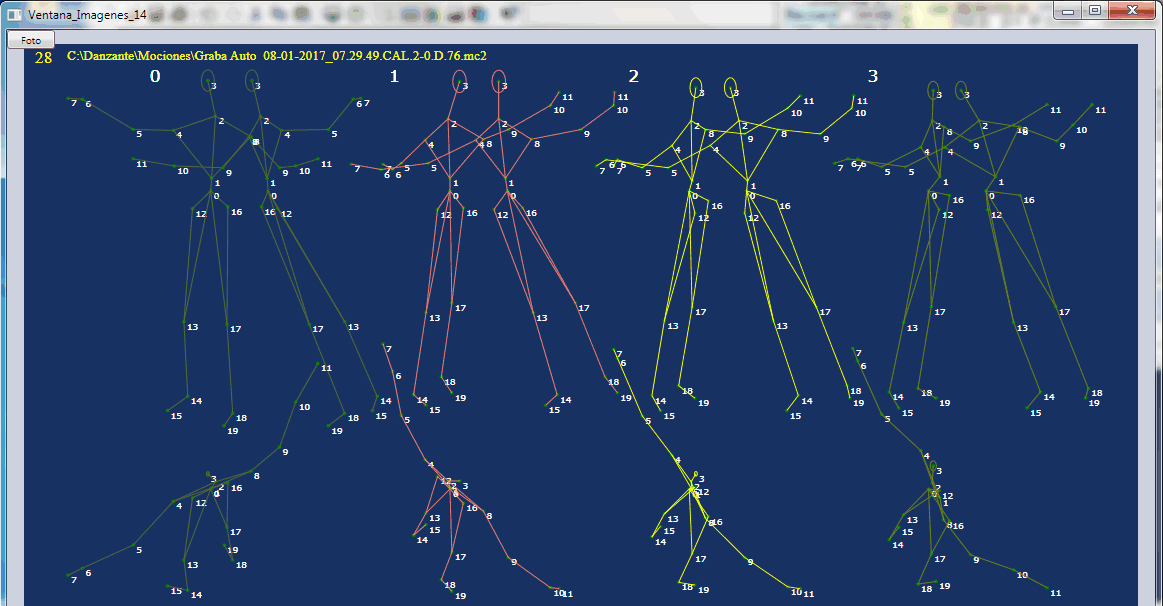
0, procede  directamente de la cámara 0.

1, procede  directamente de la cámara 1.

2, es la optimizada a partir de 1 y 3.

3, es la rotada de 0.

Se comtempla en las tres forogramas del cuadro, tres cuadros contiguos, en los que se observba ekl referido salto en el central, cuadro 27, entre lel precdente y el siguinet, silimares en posicion.

 

Más abajo se presenta los resultados numéricos de la optimización de cada cuadro, con dos procedimientos de búsqueda lineal , con resultado similar. Vemos que los problemas comienzan en el cuadro anterior al del salto, el 26, el cual sabemos que intervienen en el proceso del cuadro siguiente, el 27, porque se parte de él para buscar. Su influencia es sin embargo secundaria, únicamnet reduce lel número de pasos de la búsqueda. De modo que podemos partir del promedio del cuadro presente, el 27, cuando el procedente del anterior, el 26, encuentre problemas. Además este cambio alternatico puede hacers en tiempo real.

 

Sólo resta establecer un criterio de salto, par que lo perciba  igual que el ojo. Ello puede basarse en la distancia entre cuadros contiguos, o en los valores.

 

pero, observando los datos en la ventan de informaciones correspondientes al cuadro 26,

 

 

Comienzan Iteraciones para cuadro 26       Iteración 2   Pesos de cada articulación en cada esqueleto: Arti.   00  01  02  03  04  05  06  07  08  09  10  11  12  13  14  15  16  17  18  19  Media  Esque 1 1   1   1   1   1   1   1   1   1   1   1   1   1   1   1   1   1   1   1   1   1,00 Esque 2 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 Capta 1 2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    Capta 2 0    0    0    0    0    0    0    0    0    0    0    0    0    0    0    0    0    0    0    0       Dp incremental en mm: Arti.   00  01  02  03  04  05  06  07  08  09  10  11  12  13  14  15  16  17  18  19 dpco 1 -06  -14  -20  05  -40  -02  31  40  54  14  12  -19  -86  -02  -01  -05  -14  -07  08  -16  dpco 2 09  -08  04  12  16  01  -15  -25  -61  00  07  -09  08  19  -09  -13  -29  10  25  05  dpco 3 -11  -13  -04  31  27  27  01  08  -56  01  07  -04  -60  -10  -04  -22  -52  -15  -15  14     Lambdas Total x y z: -1,08 -2,78 -0,47 0,45

 

 

Comienzan Iteraciones para cuadro 25       Iteración 2   Pesos de cada articulacion en cada esqueleto: Arti.   00   01   02   03   04   05   06   07   08   09   10   11   12   13   14   15   16   17   18   19  Media  Esque 1 31 77 24 50 48 13 00 00 11 78 93 87 18 23 71 11 35 11 37 41 38 Esque 2 69 23 76 50 52 87 1,00 1,00 89 22 07 13 82 77 29 89 65 89 63 59 62 Capta 1 2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    Capta 2 2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2       Dp incremental en mm: Arti.   00  01  02  03  04  05  06  07  08  09  10  11  12  13  14  15  16  17  18  19 dpco 1 01  00  -02  00  -01  -03  -04  08  03  00  -04  01  01  00  00  34  00  -05  -05  00  dpco 2 -04  03  02  03  02  04  -03  -01  03  03  -04  01  -02  06  05  02  -02  07  10  01  dpco 3 02  00  -01  -01  -01  -10  10  00  04  -01  -04  00  05  03  00  13  02  -07  -04  01     Lambdas Total x y z: 0,27 1,61 1,15 0,46   Dura calculo dp, lambda: 2   OPTIMIZO GLOBAL tres puntos  Lin.Srch. Vez  Sal    Incr   √J1m:     √J0m:     √Mm:     λ:  |dp|m: dpmedia pendiente: mm             01  100,0  1,0   30,614    30,062    11,169  0,27    0,052    0,0522    0,342  mm 0             02  100,0  1,0   30,349    29,853    10,560  0,27    0,052    0,0522    0,299  mm 0             03  100,0  1,0   30,123    29,678    9,967  0,27    0,052    0,0522    0,256  mm 0             04  100,0  1,0   29,937    29,539    9,396  0,27    0,052    0,0522    0,211  mm 0             05  100,0  1,0   29,792    29,437    8,855  0,27    0,052    0,0522    0,165  mm 0             06  100,0  1,0   29,689    29,372    8,355  0,27    0,052    0,0522    0,117  mm 0             07  100,0  1,0   29,627    29,343    7,906  0,27    0,052    0,0522    0,069  mm 0             08  100,0  1,0   29,609    29,352    7,521  0,27    0,052    0,0522    0,021  mm 0             09  100,0  1,0   29,635    29,398    7,217  0,27    0,052    0,0522  -  0,029  mm 0             10  50,0  1,0   29,613    29,343    7,705  0,27  -  0,052  -  0,0522    0,024  mm 0   ****  Opti. Itera:2 Fecha:10. 6h 24m 8 Sal Fin:50,00 Ini √J1m:31,2532 Fin √J1m:29,6130 Decr. √J1m:1,6402 mm ***     OPTIMIZO GLOBAL elijo sentido solo principio D:  Lin.Srch. Vez  Sal    Incr   √J1m:     √J0m:     √Mm:     λ:  |dp|m: dpmedia pendiente: mm             01  100,0  1,0   30,915    30,307    11,790  0,27  0,052   0,382    mm 0             02  100,0  1,0   30,614    30,062    11,169  0,27  0,052   0,342    mm 0             03  100,0  1,0   30,349    29,853    10,560  0,27  0,052   0,299    mm 0             04  100,0  1,0   30,123    29,678    9,967  0,27  0,052   0,256    mm 0             05  100,0  1,0   29,937    29,539    9,396  0,27  0,052   0,211    mm 0             06  100,0  1,0   29,792    29,437    8,855  0,27  0,052   0,165    mm 0             07  100,0  1,0   29,689    29,372    8,355  0,27  0,052   0,117    mm 0             08  100,0  1,0   29,627    29,343    7,906  0,27  0,052   0,069    mm 0             09  100,0  1,0   29,609    29,352    7,521  0,27  0,052   0,021    mm 0             11  50,0  1,0   29,617    29,370    7,358  0,27  -0,026   0,041    mm 0             12  50,0  1,0   29,609    29,352    7,521  0,27  -0,026   0,016    mm 0             14  25,0  1,0   29,610    29,347    7,611  0,27  0,013   0,014    mm 0             15  25,0  1,0   29,609    29,352    7,521  0,27  0,013   0,002    mm 0             17  12,5  1,0   29,610    29,356    7,479  0,27  -0,007   0,013    mm 0             18  12,5  1,0   29,609    29,352    7,521  0,27  -0,007   0,007    mm 0             19  12,5  1,0   29,609    29,349    7,565  0,27  -0,007   0,001    mm 0             21  6,3  1,0   29,609    29,348    7,588  0,27  0,003   0,007    mm 0             22  6,3  1,0   29,609    29,349    7,565  0,27  0,003   0,004    mm 0             23  6,3  1,0   29,609    29,351    7,543  0,27  0,003   0,001    mm 0             25  3,1  1,0   29,609    29,351    7,532  0,27  -0,002   0,003    mm 0             26  3,1  1,0   29,609    29,351    7,543  0,27  -0,002   0,002    mm 0             27  3,1  1,0   29,609    29,350    7,554  0,27  -0,002   0,000    mm 0             29  1,6  1,0   29,609    29,349    7,560  0,27  0,001   0,002    mm 0             30  1,6  1,0   29,609    29,350    7,554  0,27  0,001   0,001    mm 0             31  1,6  1,0   29,609    29,350    7,549  0,27  0,001   0,000    mm 0   ****  Opti. Itera:2 Fecha:10. 6h 24m 8 Sal Fin:0,78 Ini √J1m:31,2532 Fin √J1m:29,6092 Decr. √J1m:1,6440 mm Dura:0 ms ***   Dura todo: 169 Optimizado Cuadro 25 Distancia Esque. Antes y Despues Retoque:9,00 Distancias Despues con p y q: 45,00 41,00 mm Duraciones: calculo dp 0 Toda la optimización 169 ms     Comienzan Iteraciones para cuadro 26       Iteración 2   Pesos de cada articulacion en cada esqueleto: Arti.   00   01   02   03   04   05   06   07   08   09   10   11   12   13   14   15   16   17   18   19  Media  Esque 1 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 Esque 2 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 Capta 1 2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    Capta 2 0    0    0    0    0    0    0    0    0    0    0    0    0    0    0    0    0    0    0    0       Dp incremental en mm: Arti.   00  01  02  03  04  05  06  07  08  09  10  11  12  13  14  15  16  17  18  19 dpco 1 -06  -14  -20  05  -40  -02  31  40  54  14  12  -19  -86  -02  -01  -05  -14  -07  08  -16  dpco 2 09  -08  04  12  16  01  -15  -25  -61  00  07  -09  08  19  -09  -13  -29  10  25  05  dpco 3 -11  -13  -04  31  27  27  01  08  -56  01  07  -04  -60  -10  -04  -22  -52  -15  -15  14     Lambdas Total x y z: -1,08 -2,78 -0,47 0,45   Dura calculo dp, lambda: 8   OPTIMIZO GLOBAL tres puntos  Lin.Srch. Vez  Sal    Incr   √J1m:     √J0m:     √Mm:     λ:  |dp|m: dpmedia pendiente: mm             01  100,0  1,0   35,581    36,439    7,559  -1,08    0,217    0,2166    0,986  mm 0             02  100,0  1,0   31,152    32,273    8,104  -1,08    0,217    0,2166    0,938  mm 0             03  100,0  1,0   26,576    28,156    8,940  -1,08    0,217    0,2166    0,884  mm 0             04  100,0  1,0   21,743    24,115    10,025  -1,08    0,217    0,2166    0,823  mm 0             05  100,0  1,0   16,399    20,194    11,328  -1,08    0,217    0,2166    0,755  mm 0             06  100,0  1,0   9,669    16,482    12,831  -1,08    0,217    0,2166    0,681  mm 0             07  100,0  1,0 NeuN  13,153    14,517  -1,08    0,217    0,2166    0,601  mm 0             08  100,0  1,0 NeuN  10,578    16,376  -1,08    0,217    0,2166    0,517  mm 0             09  100,0  1,0 NeuN  9,397    18,395  -1,08    0,217    0,2166    0,431  mm 0             10  100,0  1,0 NeuN  10,112    20,563  -1,08    0,217    0,2166    0,343  mm 0             11  100,0  1,0 NeuN  12,399    22,868  -1,08    0,217    0,2166    0,257  mm 0             12  100,0  1,0 NeuN  15,581    25,301  -1,08    0,217    0,2166    0,173  mm 0             13  100,0  1,0 NeuN  19,217    27,850  -1,08    0,217    0,2166    0,093  mm 0             14  100,0  1,0 NeuN  23,095    30,507  -1,08    0,217    0,2166    0,017  mm 0             15  100,0  1,0 NeuN  27,111    33,263  -1,08    0,217    0,2166  -  0,053  mm 0             16  50,0  1,0 NeuN  21,134    29,166  -1,08  -  0,217  -  0,2166    0,053  mm 0             17  25,0  1,0 NeuN  22,110    29,833  -1,08    0,217    0,2166    0,002  mm 0             18  12,5  1,0 NeuN  21,621    29,499  -1,08  -  0,217  -  0,2166    0,000  mm 0   ****  Opti. Itera:2 Fecha:10. 6h 24m 9 Sal Fin:12,50 Ini √J1m:44,1752 Fin √J1m:NeuN Decr. √J1m:NeuN mm ***   OPTIMIZO GLOBAL elijo sentido solo principio D:  Lin.Srch. Vez  Sal    Incr   √J1m:     √J0m:     √Mm:     λ:  |dp|m: dpmedia pendiente: mm             01  100,0  1,0   39,913    40,641    7,358  -1,08  0,217   1,027    mm 0             02  100,0  1,0   35,581    36,439    7,559  -1,08  0,217   0,986    mm 0             03  100,0  1,0   31,152    32,273    8,104  -1,08  0,217   0,938    mm 0             04  100,0  1,0   26,576    28,156    8,940  -1,08  0,217   0,884    mm 0             05  100,0  1,0   21,743    24,115    10,025  -1,08  0,217   0,823    mm 0             06  100,0  1,0   16,399    20,194    11,328  -1,08  0,217   0,755    mm 0             07  100,0  1,0   9,669    16,482    12,831  -1,08  0,217   0,681    mm 0             08  100,0  1,0 NeuN  13,153    14,517  -1,08  0,217   0,601    mm 0             09  100,0  1,0 NeuN  10,578    16,376  -1,08  0,217   0,517    mm 0             10  100,0  1,0 NeuN  9,397    18,395  -1,08  0,217   0,431    mm 0             11  100,0  1,0 NeuN  10,112    20,563  -1,08  0,217   0,343    mm 0             12  100,0  1,0 NeuN  12,399    22,868  -1,08  0,217   0,257    mm 0             13  100,0  1,0 NeuN  15,581    25,301  -1,08  0,217   0,173    mm 0             14  100,0  1,0 NeuN  19,217    27,850  -1,08  0,217   0,093    mm 0             15  100,0  1,0 NeuN  23,095    30,507  -1,08  0,217   0,017    mm 0             17  50,0  1,0 NeuN  25,090    31,873  -1,08  -0,108   0,069    mm 0             18  50,0  1,0 NeuN  23,095    30,507  -1,08  -0,108   0,036    mm 0             19  50,0  1,0 NeuN  21,134    29,166  -1,08  -0,108   0,001    mm 0             21  25,0  1,0 NeuN  20,169    28,505  -1,08  0,054   0,045    mm 0             22  25,0  1,0 NeuN  21,134    29,166  -1,08  0,054   0,026    mm 0             23  25,0  1,0 NeuN  22,110    29,833  -1,08  0,054   0,008    mm 0             25  12,5  1,0 NeuN  22,601    30,169  -1,08  -0,027   0,014    mm 0             26  12,5  1,0 NeuN  22,110    29,833  -1,08  -0,027   0,005    mm 0             28  6,3  1,0 NeuN  21,865    29,666  -1,08  0,014   0,006    mm 0             29  6,3  1,0 NeuN  22,110    29,833  -1,08  0,014   0,001    mm 0             31  3,1  1,0 NeuN  22,232    29,917  -1,08  -0,007   0,004    mm 0             32  3,1  1,0 NeuN  22,110    29,833  -1,08  -0,007   0,002    mm 0             34  1,6  1,0 NeuN  22,049    29,791  -1,08  0,003   0,001    mm 0   ****  Opti. Itera:2 Fecha:10. 6h 24m 9 Sal Fin:0,78 Ini √J1m:44,1752 Fin √J1m:NeuN Decr. √J1m:NeuN Dura:0 ms ***     Dura todo: 188 Optimizado Cuadro 26 Distancia Esque. Antes y Despues Retoque:65,00 Distancias Despues con p y q: 22,00 93,00 mm Duraciones: calculo dp 0 Toda la optimización 188 ms     Comienzan Iteraciones para cuadro 27       Iteración 2   Pesos de cada articulacion en cada esqueleto: Arti.   00   01   02   03   04   05   06   07   08   09   10   11   12   13   14   15   16   17   18   19  Media  Esque 1 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 Esque 2 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 Capta 1 0    0    0    0    0    0    0    0    0    0    0    0    0    0    0    0    0    0    0    0    Capta 2 2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2       Dp incremental en mm: Arti.   00  01  02  03  04  05  06  07  08  09  10  11  12  13  14  15  16  17  18  19 dpco 1 32  65  06  -14  108  09  -44  -37  -82  -61  -43  19  130  06  -05  -14  28  16  -11  40  dpco 2 30  -13  05  -31  -33  -04  02  19  72  -31  -119  -52  -35  -14  12  07  60  -11  -41  -24  dpco 3 34  63  -12  -82  -56  -03  -16  37  61  23  -43  -85  79  08  33  13  108  16  23  -38     Lambdas Total x y z: -0,68 -0,18 -0,40 -0,06   Dura calculo dp, lambda: 2   OPTIMIZO GLOBAL tres puntos  Lin.Srch. Vez  Sal    Incr   √J1m:     √J0m:     √Mm:     λ:  |dp|m: dpmedia pendiente: mm             01  100,0  1,0   72,714    76,231    27,712  -0,68    0,416    0,4165    1,239  mm 0             02  100,0  1,0   64,819    68,625    27,283  -0,68    0,416    0,4165    1,205  mm 0             03  100,0  1,0   56,918    61,206    27,246  -0,68    0,416    0,4165    1,162  mm 0             04  100,0  1,0   49,022    54,054    27,571  -0,68    0,416    0,4165    1,109  mm 0             05  100,0  1,0   41,138    47,288    28,233  -0,68    0,416    0,4165    1,041  mm 0             06  100,0  1,0   33,268    41,101    29,219  -0,68    0,416    0,4165    0,953  mm 0             07  100,0  1,0   25,400    35,793    30,530  -0,68    0,416    0,4165    0,837  mm 0             08  100,0  1,0   17,489    31,808    32,165  -0,68    0,416    0,4165    0,684  mm 0             09  100,0  1,0   9,312    29,684    34,122  -0,68    0,416    0,4165    0,484  mm 0             10  100,0  1,0 NeuN  29,820    36,391  -0,68    0,416    0,4165    0,238  mm 0             11  100,0  1,0   0,773    32,189    38,957  -0,68    0,416    0,4165  -  0,036  mm 0             12  50,0  1,0 NeuN  30,746    37,638  -0,68    0,416    0,4165    0,052  mm 0             13  25,0  1,0 NeuN  30,215    37,005  -0,68  -  0,416  -  0,4165    0,000  mm 0             14  12,5  1,0 NeuN  30,464    37,319  -0,68    0,416    0,4165    0,002  mm 0             15  6,3  1,0 NeuN  30,335    37,162  -0,68  -  0,416  -  0,4165    0,000  mm 0   ****  Opti. Itera:2 Fecha:10. 6h 24m 9 Sal Fin:6,25 Ini √J1m:88,4536 Fin √J1m:NeuN Decr. √J1m:NeuN mm ***     OPTIMIZO GLOBAL elijo sentido solo principio D:  Lin.Srch. Vez  Sal    Incr   √J1m:     √J0m:     √Mm:     λ:  |dp|m: dpmedia pendiente: mm             01  100,0  1,0   80,594    83,976    28,558  -0,68  0,416   1,267    mm 0             02  100,0  1,0   72,714    76,231    27,712  -0,68  0,416   1,239    mm 0             03  100,0  1,0   64,819    68,625    27,283  -0,68  0,416   1,205    mm 0             04  100,0  1,0   56,918    61,206    27,246  -0,68  0,416   1,162    mm 0             05  100,0  1,0   49,022    54,054    27,571  -0,68  0,416   1,109    mm 0             06  100,0  1,0   41,138    47,288    28,233  -0,68  0,416   1,041    mm 0             07  100,0  1,0   33,268    41,101    29,219  -0,68  0,416   0,953    mm 0             08  100,0  1,0   25,400    35,793    30,530  -0,68  0,416   0,837    mm 0             09  100,0  1,0   17,489    31,808    32,165  -0,68  0,416   0,684    mm 0             10  100,0  1,0   9,312    29,684    34,122  -0,68  0,416   0,484    mm 0             11  100,0  1,0 NeuN  29,820    36,391  -0,68  0,416   0,238    mm 0             13  50,0  1,0 NeuN  30,746    37,638  -0,68  -0,208   0,104    mm 0             15  25,0  1,0 NeuN  30,215    37,005  -0,68  0,104   0,068    mm 0             17  12,5  1,0 NeuN  30,464    37,319  -0,68  -0,052   0,019    mm 0             19  6,3  1,0 NeuN  30,335    37,162  -0,68  0,026   0,024    mm 0             20  6,3  1,0 NeuN  30,464    37,319  -0,68  0,026   0,007    mm 0             22  3,1  1,0 NeuN  30,531    37,399  -0,68  -0,013   0,014    mm 0             23  3,1  1,0 NeuN  30,464    37,319  -0,68  -0,013   0,006    mm 0             25  1,6  1,0 NeuN  30,431    37,280  -0,68  0,007   0,005    mm 0             26  1,6  1,0 NeuN  30,464    37,319  -0,68  0,007   0,001    mm 0   ****  Opti. Itera:2 Fecha:10. 6h 24m 9 Sal Fin:0,78 Ini √J1m:88,4536 Fin √J1m:NeuN Decr. √J1m:NeuN Dura:0 ms ***     Dura todo: 182 Optimizado Cuadro 27 Distancia Esque. Antes y Despues Retoque:96,00 Distancias Despues con p y q: 82,00 28,00 mm Duraciones: calculo dp 0 Toda la optimización 182 ms     Comienzan Iteraciones para cuadro 28       Iteración 2   Pesos de cada articulacion en cada esqueleto: Arti.   00   01   02   03   04   05   06   07   08   09   10   11   12   13   14   15   16   17   18   19  Media  Esque 1 0,38 0,73 0,26 0,50 0,50 0,22 0,00 0,00 0,10 0,73 0,94 0,83 0,21 0,25 0,77 0,08 0,25 0,11 0,39 0,40 0,38 Esque 2 0,62 0,27 0,74 0,50 0,50 0,78 1,00 1,00 0,90 0,27 0,06 0,17 0,79 0,75 0,23 0,92 0,75 0,89 0,61 0,60 0,62 Capta 1 2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    Capta 2 2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2       Dp incremental en mm: Arti.   00  01  02  03  04  05  06  07  08  09  10  11  12  13  14  15  16  17  18  19 dpco 1 -29  -54  18  03  -69  -08  -22  -16  -01  43  24  -28  -23  -08  04  -08  -08  -10  02  -25  dpco 2 -35  17  -10  09  09  -09  49  -08  03  26  121  70  20  -17  -03  -02  -13  -08  08  13  dpco 3 -25  -50  14  46  22  -26  -02  -20  05  -26  37  34  -05  00  -36  -02  -36  -03  -07  16     Lambdas Total x y z: -0,11 0,98 0,08 0,22   Dura calculo dp, lambda: 4   OPTIMIZO GLOBAL tres puntos  Lin.Srch. Vez  Sal    Incr   √J1m:     √J0m:     √Mm:     λ:  |dp|m: dpmedia pendiente: mm             01  100,0  1,0   51,644    52,864    33,818  -0,11    0,258    0,2580    1,055  mm 0             02  100,0  1,0   47,589    48,785    32,154  -0,11    0,258    0,2580    1,001  mm 0             03  100,0  1,0   43,756    44,928    30,540  -0,11    0,258    0,2580    0,936  mm 0             04  100,0  1,0   40,210    41,357    28,980  -0,11    0,258    0,2580    0,857  mm 0             05  100,0  1,0   37,030    38,151    27,497  -0,11    0,258    0,2580    0,761  mm 0             06  100,0  1,0   34,317    35,409    26,140  -0,11    0,258    0,2580    0,644  mm 0             07  100,0  1,0   32,185    33,247    24,976  -0,11    0,258    0,2580    0,503  mm 0             08  100,0  1,0   30,750    31,783    24,085  -0,11    0,258    0,2580    0,337  mm 0             09  100,0  1,0   30,107    31,116    23,550  -0,11    0,258    0,2580    0,151  mm 0             10  100,0  1,0   30,303    31,297    23,441  -0,11    0,258    0,2580  -  0,046  mm 0             11  50,0  1,0   30,100    31,100    23,439  -0,11    0,258    0,2580    0,048  mm 0             12  25,0  1,0   30,077    31,081    23,481  -0,11  -  0,258  -  0,2580    0,005  mm 0             13  12,5  1,0   30,082    31,084    23,456  -0,11    0,258    0,2580  -  0,001  mm 0   ****  Opti. Itera:2 Fecha:10. 6h 24m 10 Sal Fin:12,50 Ini √J1m:60,2329 Fin √J1m:30,0818 Decr. √J1m:30,1511 mm ***     OPTIMIZO GLOBAL elijo sentido solo principio D:  Lin.Srch. Vez  Sal    Incr   √J1m:     √J0m:     √Mm:     λ:  |dp|m: dpmedia pendiente: mm             01  100,0  1,0   55,872    57,118    35,546  -0,11  0,258   1,100    mm 0             02  100,0  1,0   51,644    52,864    33,818  -0,11  0,258   1,055    mm 0             03  100,0  1,0   47,589    48,785    32,154  -0,11  0,258   1,001    mm 0             04  100,0  1,0   43,756    44,928    30,540  -0,11  0,258   0,936    mm 0             05  100,0  1,0   40,210    41,357    28,980  -0,11  0,258   0,857    mm 0             06  100,0  1,0   37,030    38,151    27,497  -0,11  0,258   0,761    mm 0             07  100,0  1,0   34,317    35,409    26,140  -0,11  0,258   0,644    mm 0             08  100,0  1,0   32,185    33,247    24,976  -0,11  0,258   0,503    mm 0             09  100,0  1,0   30,750    31,783    24,085  -0,11  0,258   0,337    mm 0             10  100,0  1,0   30,107    31,116    23,550  -0,11  0,258   0,151    mm 0             12  50,0  1,0   30,100    31,100    23,439  -0,11  -0,129   0,095    mm 0             14  25,0  1,0   30,077    31,081    23,481  -0,11  0,064   0,028    mm 0             16  12,5  1,0   30,082    31,084    23,456  -0,11  -0,032   0,034    mm 0             17  12,5  1,0   30,077    31,081    23,481  -0,11  -0,032   0,009    mm 0             19  6,3  1,0   30,080    31,085    23,496  -0,11  0,016   0,022    mm 0             20  6,3  1,0   30,077    31,081    23,481  -0,11  0,016   0,010    mm 0             22  3,1  1,0   30,077    31,081    23,474  -0,11  -0,008   0,006    mm 0             24  1,6  1,0   30,077    31,081    23,477  -0,11  0,004   0,002    mm 0   ****  Opti. Itera:2 Fecha:10. 6h 24m 10 Sal Fin:0,78 Ini √J1m:60,2329 Fin √J1m:30,0769 Decr. √J1m:30,1560 mm Dura:0 ms ***     Dura todo: 179 Optimizado Cuadro 28 Distancia Esque. Antes y Despues Retoque:53,00 Distancias Despues con p y q: 53,00 46,00 mm Duraciones: calculo dp 0 Toda la optimización 179 ms

Comienzan Iteraciones para cuadro 25       Iteración 2   Pesos de cada articulacion en cada esqueleto: Arti.   00   01   02   03   04   05   06   07   08   09   10   11   12   13   14   15   16   17   18   19  Media  Esque 1 0,31 0,77 0,24 0,50 0,48 0,13 0,00 0,00 0,11 0,78 0,93 0,87 0,18 0,23 0,71 0,11 0,35 0,11 0,37 0,41 0,38 Esque 2 0,69 0,23 0,76 0,50 0,52 0,87 1,00 1,00 0,89 0,22 0,07 0,13 0,82 0,77 0,29 0,89 0,65 0,89 0,63 0,59 0,62 Capta 1 2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    Capta 2 2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2       Dp incremental en mm: Arti.   00  01  02  03  04  05  06  07  08  09  10  11  12  13  14  15  16  17  18  19 dpco 1 -01  -16  08  -01  01  00  -23  -19  -30  17  28  -03  34  -01  -01  04  05  03  -02  03  dpco 2 -01  -05  01  -01  -01  -03  10  11  27  09  20  18  00  -10  -06  03  08  -04  -08  -02  dpco 3 -01  -15  02  00  -02  -07  -20  -04  16  01  36  31  21  04  -03  08  12  04  03  -05     Lambdas Total x y z: -0,01 0,08 0,87 0,48   Dura calculo dp, lambda: 2   OPTIMIZO GLOBAL tres puntos  Lin.Srch. Vez  Sal    Incr   √J1m:     √J0m:     √Mm:     λ:  |dp|m: dpmedia pendiente: mm             01  100,0  1,0   34,323    34,338    8,506  -0,01    0,113    0,1133    0,661  mm 0             02  100,0  1,0   33,167    33,183    8,505  -0,01    0,113    0,1133    0,603  mm 0             03  100,0  1,0   32,130    32,147    8,696  -0,01    0,113    0,1133    0,539  mm 0             04  100,0  1,0   31,222    31,241    9,067  -0,01    0,113    0,1133    0,470  mm 0             05  100,0  1,0   30,455    30,477    9,598  -0,01    0,113    0,1133    0,395  mm 0             06  100,0  1,0   29,840    29,866    10,265  -0,01    0,113    0,1133    0,316  mm 0             07  100,0  1,0   29,387    29,417    11,046  -0,01    0,113    0,1133    0,232  mm 0             08  100,0  1,0   29,104    29,139    11,921  -0,01    0,113    0,1133    0,145  mm 0             09  100,0  1,0   28,994    29,035    12,871  -0,01    0,113    0,1133    0,056  mm 0             10  100,0  1,0   29,060    29,108    13,885  -0,01    0,113    0,1133  -  0,034  mm 0             11  50,0  1,0   29,005    29,049    13,371  -0,01    0,113    0,1133    0,028  mm 0   ****  Opti. Itera:2 Fecha:11. 8h 21m 51 Sal Fin:50,00 Ini √J1m:36,9420 Fin √J1m:29,0051 Decr. √J1m:7,9368 mm ***     Dura todo: 58 Optimizado Cuadro 25 Distancia Esque. Antes y Despues Retoque:23,00 Distancias Despues con p y q: 46,00 41,00 mm Duraciones: calculo dp 0 Toda la optimización 58 ms     Comienzan Iteraciones para cuadro 26       Iteración 2   Pesos de cada articulacion en cada esqueleto: Arti.   00   01   02   03   04   05   06   07   08   09   10   11   12   13   14   15   16   17   18   19  Media  Esque 1 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 Esque 2 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 Capta 1 2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    Capta 2 0    0    0    0    0    0    0    0    0    0    0    0    0    0    0    0    0    0    0    0       Dp incremental en mm: Arti.   00  01  02  03  04  05  06  07  08  09  10  11  12  13  14  15  16  17  18  19 dpco 1 -02  -28  -16  07  -41  00  27  06  38  40  18  -10  -54  00  00  11  -18  -05  06  -15  dpco 2 -01  -07  02  13  13  03  -20  -28  -39  20  24  21  -02  20  -20  -09  -27  07  25  04  dpco 3 -02  -27  -08  32  21  12  07  05  -23  05  30  36  -33  -09  -09  -14  -45  -09  -13  16     Lambdas Total x y z: -0,58 -0,22 0,08 -0,23   Dura calculo dp, lambda: 1   OPTIMIZO GLOBAL tres puntos  Lin.Srch. Vez  Sal    Incr   √J1m:     √J0m:     √Mm:     λ:  |dp|m: dpmedia pendiente: mm             01  100,0  1,0   29,751    30,262    7,244  -0,58    0,183    0,1828    0,905  mm 0             02  100,0  1,0   25,978    26,695    8,044  -0,58    0,183    0,1828    0,855  mm 0             03  100,0  1,0   22,070    23,157    9,179  -0,58    0,183    0,1828    0,799  mm 0             04  100,0  1,0   17,934    19,662    10,553  -0,58    0,183    0,1828    0,736  mm 0             05  100,0  1,0   13,355    16,239    12,094  -0,58    0,183    0,1828    0,665  mm 0             06  100,0  1,0   7,558    12,944    13,756  -0,58    0,183    0,1828    0,585  mm 0             07  100,0  1,0 NeuN  9,907    15,508  -0,58    0,183    0,1828    0,498  mm 0             08  100,0  1,0 NeuN  7,448    17,329  -0,58    0,183    0,1828    0,401  mm 0             09  100,0  1,0 NeuN  6,290    19,208  -0,58    0,183    0,1828    0,297  mm 0             10  100,0  1,0 NeuN  7,098    21,135  -0,58    0,183    0,1828    0,187  mm 0             11  100,0  1,0 NeuN  9,378    23,104  -0,58    0,183    0,1828    0,072  mm 0             12  100,0  1,0 NeuN  12,340    25,111  -0,58    0,183    0,1828  -  0,043  mm 0             13  50,0  1,0 NeuN  10,806    24,103  -0,58    0,183    0,1828    0,036  mm 0   ****  Opti. Itera:2 Fecha:11. 8h 21m 51 Sal Fin:50,00 Ini √J1m:37,0614 Fin √J1m:NeuN Decr. √J1m:NeuN mm ***     Dura todo: 62 Optimizado Cuadro 26 Distancia Esque. Antes y Despues Retoque:45,00 Distancias Despues con p y q: 9,00 83,00 mm Duraciones: calculo dp 0 Toda la optimización 62 ms     Comienzan Iteraciones para cuadro 27       Iteración 2   Pesos de cada articulacion en cada esqueleto: Arti.   00   01   02   03   04   05   06   07   08   09   10   11   12   13   14   15   16   17   18   19  Media  Esque 1 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 Esque 2 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 Capta 1 0    0    0    0    0    0    0    0    0    0    0    0    0    0    0    0    0    0    0    0    Capta 2 2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2       Dp incremental en mm: Arti.   00  01  02  03  04  05  06  07  08  09  10  11  12  13  14  15  16  17  18  19 dpco 1 -01  28  17  -07  40  04  -02  -16  -39  -37  -12  05  55  00  01  -12  16  05  -03  15  dpco 2 00  05  -04  -17  -18  -05  -08  05  35  -24  -56  -28  -01  -17  00  -07  28  -07  -25  -08  dpco 3 -01  27  07  -37  -25  -06  45  04  21  -07  -22  -40  33  05  11  10  42  06  12  -16     Lambdas Total x y z: 0,52 1,01 2,28 0,24   Dura calculo dp, lambda: 2   OPTIMIZO GLOBAL tres puntos  Lin.Srch. Vez  Sal    Incr   √J1m:     √J0m:     √Mm:     λ:  |dp|m: dpmedia pendiente: mm             01  100,0  1,0   31,845    30,973    10,280  0,52    0,190    0,1903    0,898  mm 0             02  100,0  1,0   28,449    27,344    10,903  0,52    0,190    0,1903    0,822  mm 0             03  100,0  1,0   25,268    23,771    11,901  0,52    0,190    0,1903    0,732  mm 0             04  100,0  1,0   22,397    20,282    13,196  0,52    0,190    0,1903    0,623  mm 0             05  100,0  1,0   19,973    16,931    14,716  0,52    0,190    0,1903    0,495  mm 0             06  100,0  1,0   18,180    13,819    16,408  0,52    0,190    0,1903    0,345  mm 0             07  100,0  1,0   17,221    11,145    18,233  0,52    0,190    0,1903    0,177  mm 0             08  100,0  1,0   17,240    9,299    20,164  0,52    0,190    0,1903  -  0,004  mm 0             09  50,0  1,0   17,104    10,086    19,187  0,52    0,190    0,1903    0,025  mm 0             10  25,0  1,0   17,131    10,586    18,707  0,52  -  0,190  -  0,1903  -  0,005  mm 0   ****  Opti. Itera:2 Fecha:11. 8h 21m 52 Sal Fin:25,00 Ini √J1m:39,0565 Fin √J1m:17,1307 Decr. √J1m:21,9258 mm ***     Dura todo: 67 Optimizado Cuadro 27 Distancia Esque. Antes y Despues Retoque:33,00 Distancias Despues con p y q: 72,00 10,00 mm Duraciones: calculo dp 0 Toda la optimización 67 ms     Comienzan Iteraciones para cuadro 28       Iteración 2   Pesos de cada articulacion en cada esqueleto: Arti.   00   01   02   03   04   05   06   07   08   09   10   11   12   13   14   15   16   17   18   19  Media  Esque 1 0,38 0,73 0,26 0,50 0,50 0,22 0,00 0,00 0,10 0,73 0,94 0,83 0,21 0,25 0,77 0,08 0,25 0,11 0,39 0,40 0,38 Esque 2 0,62 0,27 0,74 0,50 0,50 0,78 1,00 1,00 0,90 0,27 0,06 0,17 0,79 0,75 0,23 0,92 0,75 0,89 0,61 0,60 0,62 Capta 1 2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    Capta 2 2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2    2       Dp incremental en mm: Arti.   00  01  02  03  04  05  06  07  08  09  10  11  12  13  14  15  16  17  18  19 dpco 1 00  -13  06  -01  01  01  -31  -20  -34  21  25  -13  31  -02  02  -10  09  02  -01  02  dpco 2 -01  -02  -01  -02  01  -06  26  02  25  15  39  22  02  -13  -02  -08  17  -07  -09  -02  dpco 3 00  -13  02  00  02  -04  -28  12  18  05  35  01  20  03  -05  04  21  03  03  -05     Lambdas Total x y z: -0,31 -0,23 0,55 0,35   Dura calculo dp, lambda: 2   OPTIMIZO GLOBAL tres puntos  Lin.Srch. Vez  Sal    Incr   √J1m:     √J0m:     √Mm:     λ:  |dp|m: dpmedia pendiente: mm             01  100,0  1,0   36,745    36,942    6,846  -0,31    0,128    0,1275    0,733  mm 0             02  100,0  1,0   35,298    35,570    7,877  -0,31    0,128    0,1275    0,685  mm 0             03  100,0  1,0   33,947    34,332    9,208  -0,31    0,128    0,1275    0,633  mm 0             04  100,0  1,0   32,703    33,245    10,726  -0,31    0,128    0,1275    0,576  mm 0             05  100,0  1,0   31,581    32,323    12,356  -0,31    0,128    0,1275    0,515  mm 0             06  100,0  1,0   30,594    31,580    14,054  -0,31    0,128    0,1275    0,449  mm 0             07  100,0  1,0   29,756    31,030    15,793  -0,31    0,128    0,1275    0,377  mm 0             08  100,0  1,0   29,081    30,682    17,554  -0,31    0,128    0,1275    0,302  mm 0             09  100,0  1,0   28,584    30,545    19,324  -0,31    0,128    0,1275    0,221  mm 0             10  100,0  1,0   28,274    30,620    21,092  -0,31    0,128    0,1275    0,137  mm 0             11  100,0  1,0   28,161    30,906    22,851  -0,31    0,128    0,1275    0,050  mm 0             12  100,0  1,0   28,249    31,397    24,593  -0,31    0,128    0,1275  -  0,039  mm 0             13  50,0  1,0   28,179    31,126    23,724  -0,31    0,128    0,1275    0,031  mm 0   ****  Opti. Itera:2 Fecha:11. 8h 21m 52 Sal Fin:50,00 Ini √J1m:39,8811 Fin √J1m:28,1794 Decr. √J1m:11,7017 mm ***     Dura todo: 62 Optimizado Cuadro 28 Distancia Esque. Antes y Despues Retoque:31,00 Distancias Despues con p y q: 55,00 47,00 mm Duraciones: calculo dp 0 Toda la optimización 62 ms

 

Para investigar este comportamiento inesperado de nuestro algoritmo de optimizacion, representamos la gurva J1 cuyo mínimo buscamos. para el cuadro 26 observamos un comportamiento inesperado , con mínimo negativo, (izquierda) frente al habitual (derecha), con mínimo positivo:

 

 

Pero dado que J1 vale, como sabemos, Por definición, (que vemos por ejemplo, en Optimización II.Desglose de operaciones.JCISER):

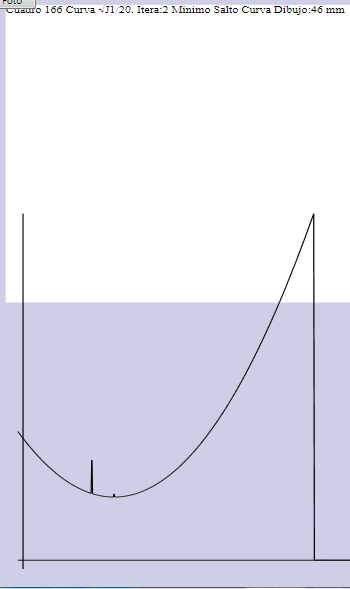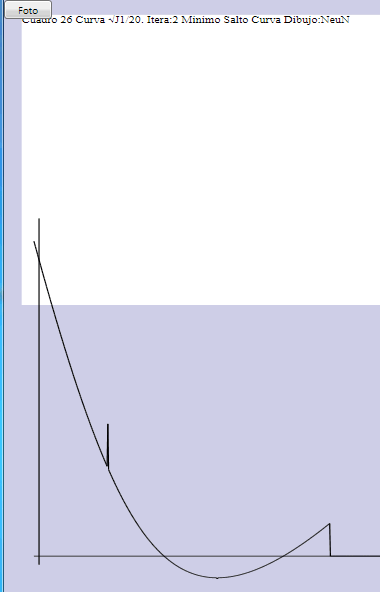
 J 1  =   J0  +  λ  M         con

 

 J₀ ({ p_i^*})  =  Σ_{i ε Sa}   w_i^A|| p_i^* -  p_i || ² + w_i^B|| p_i^*  -  (Rq_i + t ) || ²  

 

M = Σ_{i,j ε Sa}   ( || p_i^* -  p_j ||   - L_i,j ) ²

siendo J0 y M positivas, sólo puede darse ese valor negativo que aparece en la figura (el cálculo falla (símbolo NeuN) para un valor negativo excesivo del coeficiente λ .

 

Por el momento detenemos la búsqueda de mínimo cuando J1 se hace negativo, pues comprobamos que M sde hace grande, lo que aleja el optimo de las proporciones (longitudes de hueso) que intyentamos mantener en lo posible (en compromioso con los esqueletos.

 

NÓTESE QUE TODO ESTO OCURRE CUANDO UNA ESQUELETO ES NULO.

AHI HAY QUE ATACAR EL PROBLEMA.

 

Por un lado, esto no debe ocurrir.

 

Por el otro, si ocutte ese cuadro no debe intrvenor en los cálculos. Esto es f´cial en las etapas previsd (cgrabavon para la calibracipm). pro en más delicado dutante la optimizacvion en tgiempo real, porquer si no se condiera un cuaDRO    , NODE PROUCE UN hueco, un cacio que introuce cdscotinuidad en cuadro visto y y en vávulos sucesiobops, ligados como sabemos al esquleto optimixado amnterioe.

 

 

la deteccion es fácil  durante la grabacion y en dutante lalectura. así icoprramos esa informacion en los tectos de autoanalisis de cada mocion en disco:

 

Una mocion perfecta desde ese punto de vista:

/danzante/mociones/Graba Auto 13-01-2017_15.45.15.CAL.0-0.D.70.mc2 Escalas dibujo: 226 Escalas a mm: 1000
Cuadros: 200 Cámaras: 2 Retardo 1 de 2: 10 Fecha: 13/01/2017
Cuadros perdidos camaras 0, 1: 0 0 Fiabilidad media (de 0 a 2) captación cámaras 0, 1: 0 0
Cuadros defectuosos camara 0: Total 0
Cuadros defectuosos camara 1: Total 0

una menos perfecta

/danzante/mociones/Graba Auto 13-01-2017_10.43.00.CAL.1-0.D.79.mc2 Escalas dibujo: 226 Escalas a mm: 1000
Cuadros: 200 Cámaras: 2 Retardo 1 de 2: 10 Fecha: 13/01/2017
Cuadros perdidos camaras 0, 1: 1 0 Fiabilidad media (de 0 a 2) captación cámaras 0, 1: 0 0
Cuadros defectuosos camara 0: 52 Total 1
Cuadros defectuosos camara 1: 51 135 Total 2

y una imperfecta (consideramos todos los vuadros en las distancias, incluso los defectuosos

/danzante/mociones/Graba Auto 13-01-2017_11.51.45.CAL.616-507.D.204.mc2 Escalas dibujo: 226 Escalas a mm: 1000
Cuadros: 200 Cámaras: 2 Retardo 1 de 2: 10 Fecha: 13/01/2017
Cuadros perdidos camaras 0, 1: 616 507 Fiabilidad media (de 0 a 2) captación cámaras 0, 1: 0 0
Cuadros defectuosos camara 0: 20 31 39 49 53 56 60 66 76 81 84 91 94 101 124 128 138 141 146 150 165 177 182 185 192 198 Total 26
Cuadros defectuosos camara 1: 4 15 27 33 43 58 64 72 86 99 103 114 127 154 190 Total 15

Desde luego se mejoran las cosas descargando tareas del computdos: lqa captacion, guardado y procesado en tiempo real de  las emisiones de dos cámaras preciisa cuidado.

1.  ejecutar ejecutable de la operación, no debug.

2. Aliviar de aplicaciones simultáneas: cerrarlas..

3. Incluso computador ecien encendido.

4. Vestimenta masculina estrecha.

5. Suprimir llamadas a la percepción de sucesos en la aplicaci´pn: ( en VisualBasic).

6. Pero perimitiedo la interrupción de la tarea sin fin mediante otros métodos:

6.1 fin mediante valor que toma una variable, como contador número de cuadros.

7, Podría eliminarse el cuadro defectuoso o pormediar entre los contiguos la pista defectuosa (suele ser siempre sñolo una de ellas.

 

 

 

---

 

Vuelta al Principio    Última actualización: sábado, 14 de enero de 2017    Visitantes: