Proyecto Danzante. Funciones a minimizar. Naturaleza. JCISER (incluido en Danzante)

 

Má abajo recordamos la funcion J1 a minimizar. Ahora vemos la curva continua (no saltos) y suave (curvatura pequeña) de la funciona minimizar en función del valor de la variable, que es ahora el valor della coordenada (medidada) del incremento optimizado dp.

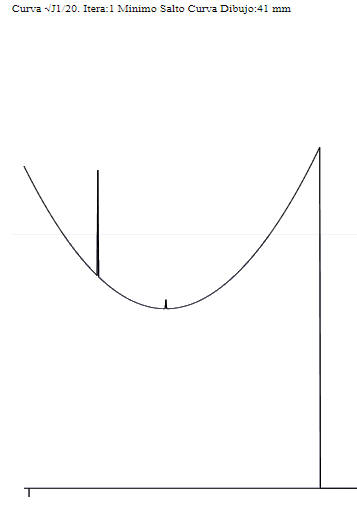
La curva de la izquierda representa la función J1 pero transformada en Raiz cuadrada de la media de esa función sobre sus articulaciones. La línea vertical es el valor 0 de la abscisa, Esta abscisa  es el incremento dp que se aplica al esqueleto compuesto del promedio de los de las dos cámaras o, cuando el algoritmo está corriendo en tiempo real, el esqueleto optimizado del cuadro anterior. Mediante esos incrementos de dp nos acercamos gradualmente, siguiendo el método de Newton Cramer (llamado en nuestro artículo Line Search), al mínimo, que representa el compromiso óptimo (para las funciones y ponderaciones adoptadas) entr elas tres funciones que tiran de ese esquleto. Promerioo pìonderado entre esquekletos de cámaras, longitudes de huesos obtenidas en calibración, y esquleto optimizado anterior que ha realizxado ese acercamiento. , y del cual se espera que sea cercano al actual, debido al coertto tiempo entre cuadros (alrededor de 30ms. La curva es mon´toma (y suave) a ambos lados del mínimo. Es dcir tamto la función como su pendiente (en valor absoluto) decrecen uniformrmrntr hasta llegar a mínimo. la variable es un vector con 60 coordenadas cuya variación produce esa ciurva suave. Otro vector cuaklquiera perdería esa cualidad suave en la curva.

 

Hay tres condiciones o gomas que tiran de cada una y de todas (su suma) :

 

1. El esqueleto optimizado anterior, que refleja la continuidad indispensable del movimiento a lo largo del tieomp (vel=despla/tiempo). empleado)

 

2. Los dos esquletos de cda cámara que tiran hacia ellos (mediante penalización de la distancia a ellos. En rfelaidad son dos gomas, cada una titando hacia sí misma

 

3. La longitud tomada como fija de los huesos (segmento que unen algunas pares de artuculaciones., conocimien to admirido en la calibracion.

 

Cualquieta de las tres presentan mínimos segen las cercanias de cda articulacion, tres posd cda coordenadas con un mínimo al condidrerar las tres al tiempo.

 

De modo que dada una situacion cualquiera. Podemos comprobar (segun sus derivadas) hacia donde moverse para disminuir las distancias 1,2,3 o mejor, su suma ponderada.

 

Por lo tanto, en esta optimización nos encontramos con unas funciones elementales por articulacion, condicente a una funcion continia paro con varios mínimos locales. Son funciones de una coordenada (x,y,z) en forma de U, con el mínimo en el monto en que el valor de la variable se acerca lo más posible al valor de esa variavle en el minimo. El valor de la funcion, la distancia cartisuina, es 0 si las trs coordednadas coinciden, y sólo una vakor menor que los vecinos cuando pasa cerca, es decir ciando la coordenada tomada como variable en este caso e coindice con el valor para el mínimo, pero las otras dos ao al meon una de ellas, no coinciden. En el espacio 3D eso ocurre ciandola disdtancla distancia es la longitud de la percpendicular desde el minimo (tres variables) a la recta de variacuion de la varibale. Ahora podemos llegar a ese minimo espacial acercándonos sucesivamente con las terwes coordenadas, una por una.

 

La suma pra todas las articulaciones nos dará una funcion (tres vamos a ver que son segun tres distancias) con varioa mínimos locañes (veiente en principio)

 

 El algorirmo pùes tendrá que decidir qué mínimos elige, sabiendo que cada uno esta relacionados con una de las articulñaciones.

 

Podemos montar un banco de trabajo que para desplazar manulamente (flechas del teclado (teclas numericas 4-6 para x; , 8-2 pra y, 9-1 ,para z. Y comprobar como varia CADA ARTI. Solo para comprobar este comportamiento supuesto del ajuste.

 

En todas, la  cercania a un minimo local no va a garantizar que sea el minomo minimorum

 

Podemos diseñar una ajuste escalonado, empezando por las cabezas de miwembro (0-1-2-3,   2-4-5-6,  er5c...) e ir ajustando cada articulacion habiendo ya situado la anetior,

 

Y timar sólo las articulaciones ya situadas ( de 0 a  i) especialmente tenien do en cunata la distancia 3.

 

Las articulaciones se irán (se irían, si todo va bien) situando sucesivamente seguiun ese orden, que es precisamente (por decision previa en Kinect) su  codigo numerico.

 

Llamaremos a este metodo el del traje a medida: vamos ajustando el traje al cuerpo articulacion a articulacion.

 

El problema de  este método es que presupone la correccion de las oprraciones anterioes a la que estamos aplicando. Presuncion que que tomn todas los metodos, que suponen casi corercta el esqueleto optimop anterios (del cuadro anterior) las longitudes de klos huesos (tiomas anteriores, en la calibracion).

 

Asi que operamos como usando una pequela base  dedatos indivisual para un esquleto deperminado, que se mueve suavemente y es 'percibido' casi bien por dis camaras simultáneas. Podemos imaginbar entonces que e4ste u otro métodops , como el global, el descrito en el artículos, presenten una límite, unas cotas de correccion, a partir de las cuales, una vez sobrepasada, no funcioe la optimizacion deseada.

 

Recordemos que no estamos 'viendo' nada, sino estimando un esquleto verosimil, que se mueva suavemente, pero no necesariamente el esqueleto del humano que 'percibimos.

 

 

 

 

 

 

erivadas vectoriales.JCISER.htm

 

derivadas vectoriales en un campo escalar, en los vectores

 Λ =  { ^δ_{/ δ p*i} ( Σ_{i,j ε Sa}   ( || p_i^* -  p_j^*  ||   - L_i,j ) ²  )  }         o sea        Λ =  {  ^δ_{/ δ p*i} M)

b_p =  - { ^δ_{/ δ p*i} Σ_i   w_i^A || p_i^* -  p_i || ² + w_i^B || p_i^*  -  (Rq_i + t ) || ² }       o sea       b_p =  { -   ^δ_{/ δ p*i}  Σ_i j₀ )

y en la matriz diagonal

H ,        con   h_i = ^δ2_{/ δ (p*i)2} ( w_i^A|| p_i^* -  p_i || ² + w_i^B|| p_i^* -  (Rq_i + t ) || ² )     o sea   h_i =  ^δ2_{/ δ p*i2}  j_0i  

 

todos ellos componentes de matrices como como

  ▼J² (X) d          y        ▼J (X)    

es decir el gradiente y el gradiente del gradiente de una función con 20 variable vectoriales, los 20 puntos de un esqueleto, y una variable más numérica, λ .

 

Vamos a ver el número, naturaleza y dimensiones de estas derivadas

 

En general los vectores anteriores tienen la disposición  ( vector fila, como veremos):

 

 {    ^{δ Σ}_{/ δ p*0}    ^{δ Σ}_{/ δ p*1    .    .    .}       ^{δ Σ}_{/ δ p*19}   }

 

en la que derivamos una cantidad Σ  numero real que es el valor escalar en ese punto respecto al que derivamos.

 

El punto en un punto en el espacio con tres dimensiones.

 

 ^{δ Σ}_{/ δ p i}    es por definición    ^{( Σ pi +Δ pi - Σ pi  )} / _{Δ pi}         y    Δ pi  es un vector 3D que desplaza p en una cierta dirección.

 

Ahora buen , el cociente nos depara algún problema de interpretación. En realidad esta derivada corresponde, engloba a 3, una por cada coordenada incrementada:

 

 ^{δ Σ}_{/ δ p i}    es por definición    { ^{( Σ pix + Δ pix - Σ pix  )} / _{Δ pix}  ,    ^{( Σ piy + Δ piy - Σ piy  )} / _{Δ piy  ,}   ^{( Σ piz + Δ piz - Σ piz  )} / _{Δ piz}  }

 

y ahora tenemos ya sólo variables numéricas: se trata de

 

un campo escalar en el espacio 3d, con 60 componentes por las que derivar, y 60 derivadas, por lo tanto.

 

Traemos de Optimizacion.JCISER.htm las consideraciones iniciales sobre este campo

 

Campo Escalar

 

3. A diferencia del campo en la calibración., que era una distancia entre esqueletos de igual forma, esqueleto rígido podemos decir, en la optimización tenemos una función distancia compleja. entre esqueletos, pero no rígidos, porque cada articulación ha de sufrir una desplazamiento (vector en el espacio) diferente del de los demás, de modo que disminuya n las distancias al par de esqueletos que vamos a componer o sintetizar en el óptimo; y simultáneamente han de mantenerse las longitudes de los huesos obtenidas en la calibración, tomadas como valores verdaderas, lo que se ha de conseguir mediante la función J1.

4. El algoritmo de acercamiento por lo tanto será más complejo. En un lugar de un sólo ciclo de acercamiento, en la que cada etapa supone la variación de 3 elementos de giro global (de todo el esqueleto) independientes, lo que permite acercamientos individuales que pueden alternarse libremente e ir acumulándose en una matriz R, tal como se realiza en en la Calibración, en la Optimización contamos con una función a minimizar, J1, que debemos evaluar en cada etapa. Y cada etapa será modificar por desplazamiento una de las articulaciones, y evaluar la repercusión en J1, que toma en cuenta todo el esqueleto, es decir todas las articulaciones.

5. Podríamos trabajar en un círculo vicioso si atendemos primero a J0 (distancia de esqueleto óptimo a los dos originales y luego a M (longitudes de huesos constantes) sin lograr un acercamiento global porque ambas funciones son en cierto modo opuestas (mejorar una supone empeorar la otra).

Por ello contamos con J1, que atiende simultáneamente a ambos requerimientos, s3egún el método descrito más arriba.

7. Nos queda entonces decidir el orden de actualización de cda articulaciones, el cual, pensamos influirá probablemente en la velocidad de convergencia del algoritmo (¿quizá en la convergencia misma --si sí o si no-- ?)

 

8. Las derivadas a anular (o minimizar) se consiguen variando una a una las componentes del parámetro variable de las que depende, sea este una matriz o un vector, comprobando qué incrementos bajan el valor de la función y eligiendo los mejores. En todos estos casos el parámetro variable es p_i^* , un vector o mejor, una conjunto de posiciones (puntos) en el espacio. De modo que los incrementos individuales (números) a probar son 6, 3 coordenadas en dos sentidos opuestos. direcciones, de los que elegimos uno, como se hacía al reunir dos esqueletos en la calibración.

8'. Sólo que es la citada calibración un desplazamiento afectaba a todos loas articulaciones simultáneamente, mientras que en este caso, hay que elegir esa direccio entre 6 para cada una de las articulaciones p* por separado, sucesivamente, en un orden todavía no considerado.**********

8". Y además el valor de la función era una cantidad inmediata, la distancia entre dos esqueletos, mientras que en esta optimización, tenemos dos funciones, J0 y M a evaluar escalonadamente (según el método) y considerar. Tres funciones, tomando el cuanta que se toma como esqueleto optimizado inicla el final del proceso de optimización en el cuadro anterior. Ese cuadro en el caso inicial, comienzo de la optimizacion tras la calibración, puede ser lógicamente el final de la calibración, el promediado del ultimo cuadro de la calibración lógicamente previo inmediatamente al primero de la optimización.

 

 

8'". Así elegimos un desplazamiento* 20 puntos = 60 incrementos individuales. Como la función J y M son sumas, una mejora en un punto mejora (disminuye) ambas expresiones. El problema es que la modificación de un punto puede repercutir en los unidos a él en el esqueleto, modificando M, medida de 'errores' en longitudes de hueso. Por ello es necesaria una búsqueda de los mejores valores en la matriz de incrementos (?????).

  

Y las derivadas

 

Derivadas

Podemos derivar a lo bruto (incrementos de función divididos por incremento de variable) o analíticamente, aplicando las leyes de la derivada de funciones compuestas:    f '=df(x)/dx;    df²⁽x)/dx=2ff ';  d²f ⁽x)/dx² =2f f ''+2 f '2

9. Así que cuando tenemos derivadas de sumas, debemos sumar y luego derivar, y no invertir ese orden, porque una variación de una p_i* pudiera afectar a más de un sumando (por ejemplo, la variación de una única articulación afectará a las longitudes de uno, dos o tres huesos, como apuntábamos en 7.

9'. Sólo tras comprobar que un desplazamiento de un punto pi no afecta a los demás podemos intercambiar eo orden de estos símbolos: derivada de suma deviene suma de derivadas, de las que todas menos i son nulas (ya que no afectan, todas las articulaciones son independientes).

10. Derivada segunda se escribe aquí como ^δ2_{/ δ p*i2}   símbolo para  ^{δ(  δ  /} δ p*i ⁾_{/ δ p*i}      es decir, derivada de la derivada

_{11. Todas estas derivadas, primeras o segundas, corresponden al mismo incremento, ya que pertenecen a una misma iteración.}

 

 

 

 

 

 

Veamos aquí Optimización. Algoritmo.

 

 

---

 

Vuelta al Principio    Última actualización: jueves, 10 de noviembre de 2016    Visitantes: