Esta página está en construcción: perdonen
los errores, repeticiones y temas inacabados.
This page is being developed: I am sorry for
errors, duplications and unfinished subjects.
Interpolation (included
in
An_aadf_pitch_estimator)
We estimate a peak situated ideally between estimated values, and will
be closer of an integer value depending of the integer value situated in
the other side of the value.
a
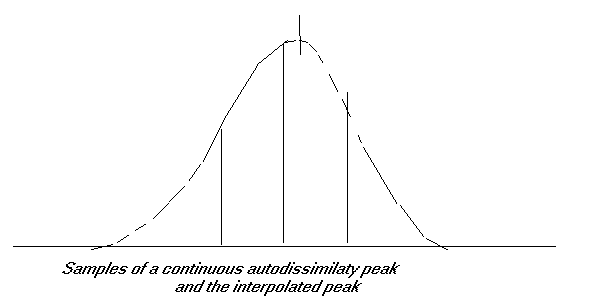 |
| Autodissimilative peak in the variable tau.
|
The exact function or curve of a ADA peak is unknown and
we used empirically round peaks as a sinus lobe , a parabola or sinc (sin (x)
divided by x).
The number of points depend on how smooth is the peak and this
smothn3ss depends on the frequency content of the signal. Usually we take 3 or
5 points to evaluate the intermediate supposed peaks. For example,
in our program ESCALA written in C++ we used successfully this algorithm,
which we also translate to VisualBasíc:
diperpro = sperpro - perpro - 1:
dif = aradfi - sradfi:
if (dif>0) then
su = aradfi - autodis:
Else:
su = sradfi - autodis:
end if
if (su>0)
d =(dif*32)/su:
if (diperpro > 0) then
d = d + (diperpro*32):
end if
e = abs(dif)/2:
Else
d = 0: e = 0:
end if
|
diperpro = sperpro - perpro - 1:
dif = aradfi - sradfi:
if (dif>0) su=aradfi-autodis:
Else: su = sradfi - autodis:
if (su>0)
{
d=(dif<<5)/su:
if (diperpro>0)
d+=(diperpro<<5):
e=abs(dif)>>1:
}
Else
{
d = 0: e = 0:
}
|
Visual Basíc
|
C ++
|
What we do is to use the maximum value and the 2 values around it
considering it to be 2 samples of an exact with infinite resolution peak.
Since we know 3 points of a parabola we can find the situation of the
maximum of this parabola and this is but we do: estimating real values of
tau intermediate between the integers points of tau.
See also some considerations on the concept of peak
(pico).
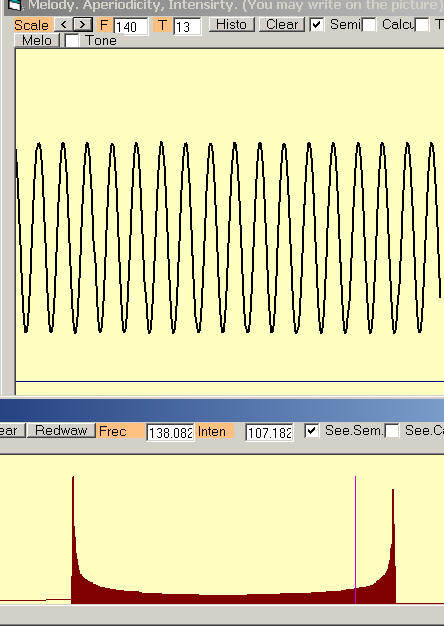
See the smoothness of this interpolation in the figure, where
a vibrato es estimated and its histogram calculated.
The vibrato is generated artificially with about half semitone
in pitch oscillation.
Hear it.
But there are other strategies for interpolation. here are
some:
1. Fractional situation of calculation moment.
If we consider fractional t, that is, a t between samples, by
admitting a linear curve (straight) between samples, any ideal sample will be
a weighted mean between the neighbors.; and the weight will be be inversely
proportional to the relative distances to each.
For fractional t, at temporal distance e (0<e<1)from the
previous, the weighted will be 1-e, and e, their sum being 1. As these weight
affect to each sample twice, one for each ideal sample, each sample in the
window will have both weighs, that is, each sample will appear in the norm
once and with its actual value. Except the extreme sample that will appear
only once. with the already seen coefficients.
The gradual displacement of the window over t will contemplate
the also gradual vanishing of the first samplke and the consequent appearing
of the one next to the last.
We know therefore the value of a discrete window in any real
value of t, coincident or intermediate between samples.
Vuelta al Principio Última
actualización:
Thursday, 21 de February de 2013
Visitantes:


