Reloj de sol Horizontal Sunclock

Venimos de ver el Reloj de sol vertical.

Todo lo dicho vale para el horizontal que presentamos. Como se supone libertad para orientarlo, lo haremos hacia el sur: es decir haremos coincidir el eje vertical del dibujo con la línea norte-sur en el suelo u otra superficie horizontal; por ejemplo, como lo hemos visto en Turquía, sobre una plataforma, para su mejor observación.

Traemos de la página citada el segundo gráfico

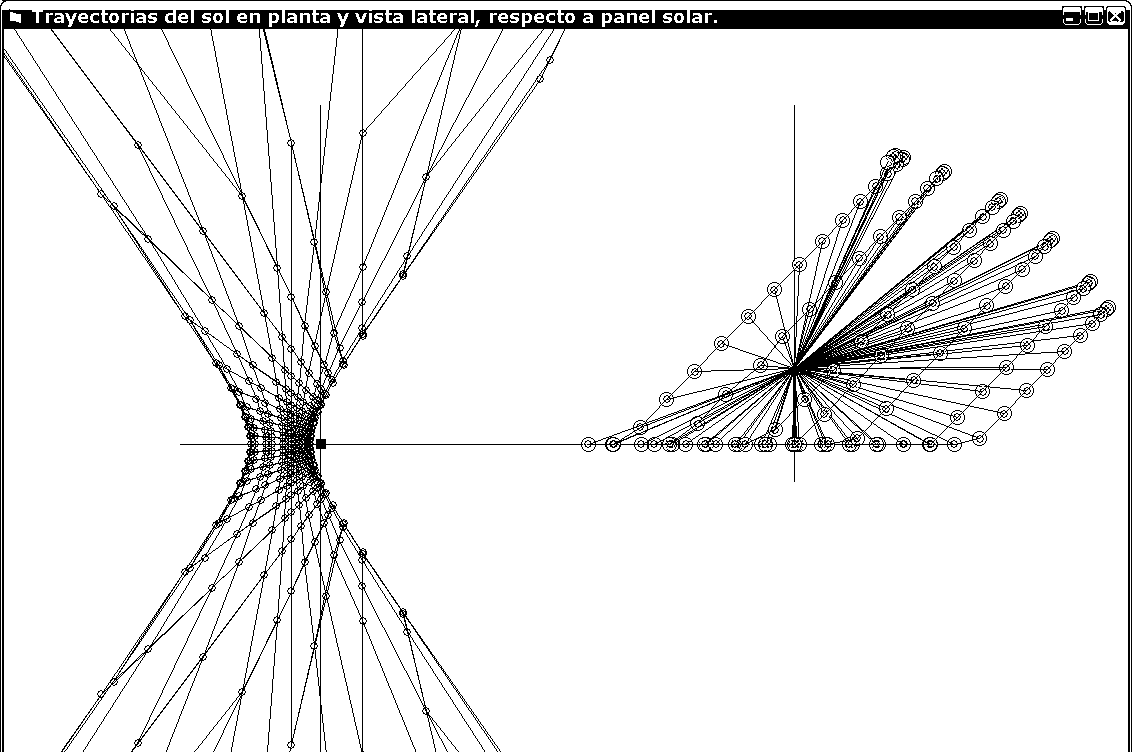
que muestra en planta y vista lateral las posiciones del sol. A partir del dibujo de la derecha, si imaginamos la línua roja como una barra, su punta arrojará una sombra que se mueve según lo hace el sol. Si la dibujamos en el suelo, a la izquierda, encontramos el dibujo de la izquierda.

Si ahora lo giramos según la dirección indicada antes queda como se ve en la figura.

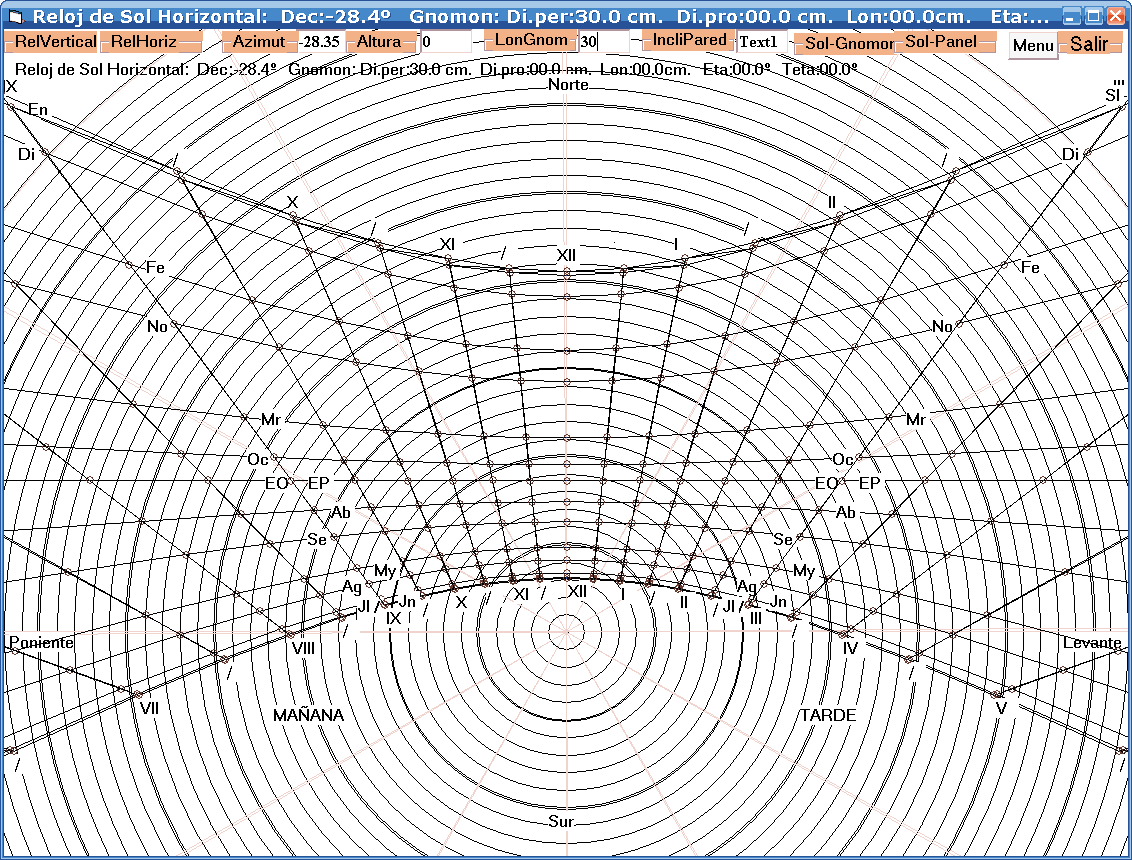
Se observan las curvas, simétricas respecto al eje Norte-Sur, correspondientes a los meses del año, comenzando por el Enero, el más alejado hacia arriba (al norte en en el suelo) y avanzando hacia el sur hasta Julio, y retrocediendo hacia el norte hasta llegar otra vez a Enero. Aparecen además las curvas curvas correspondientes a los solsticios (SI, SV), en los extremos del gráfico; y los equinoccios (EP, EO), estos dos últimos coincidentes y apareciendo como rectas horizontales (Dirección transversal, Este-Oeste)

Se representan las horas en números romanos de 0 a 12, repitiéndose por la mañana y por la tarde a cada lado del eje vertical.. Aparecen además las medias horas, con signo '/'.

Ecuaciones de la sombra del extremo del gnomon o puntero

La sombra del extremo del puntero o gnomon, describe unas curvas como las que vemos en las figuras. Las expuestas corresponden a un reloj de plano horizontal con la lamina que constituye el gnomon orientada al sur.. La curva se aproxima mediante puntos correspondientes a saltos de media hora. En esos momentos el azimut y la altura del sol dependen del lugar geográfico donde se coloca el reloj. Nuestras curvas se refieren a Madrid (España).

La ecuación de la curva queda, eliminando xx y yy y considerando x0=y0=0, en polares:

teta = az

ro =L / tan(al)

dos ecuaciones independientes. Teta es el ángulo de ro (radio_reloj) con la vertical.

az = -posi(mes, horas, 0)
al = posi(mes, horas, 1)
rr_reloj = L / Tan(al)
xx = x0 - rr_reloj * Cos( az) '
yy = y0 - rr_reloj * Sin(az) '

Ecuaciones de la sombra de gnomon en reloj horizontal (en VisualBasic)

Valores angulares en radianes.

Podemos oriental el reloj hacia el norte, al revés que antes, quedando la figura simétrica:

Un poco de geometría

Si ampliamos la extensión vista del reloj:

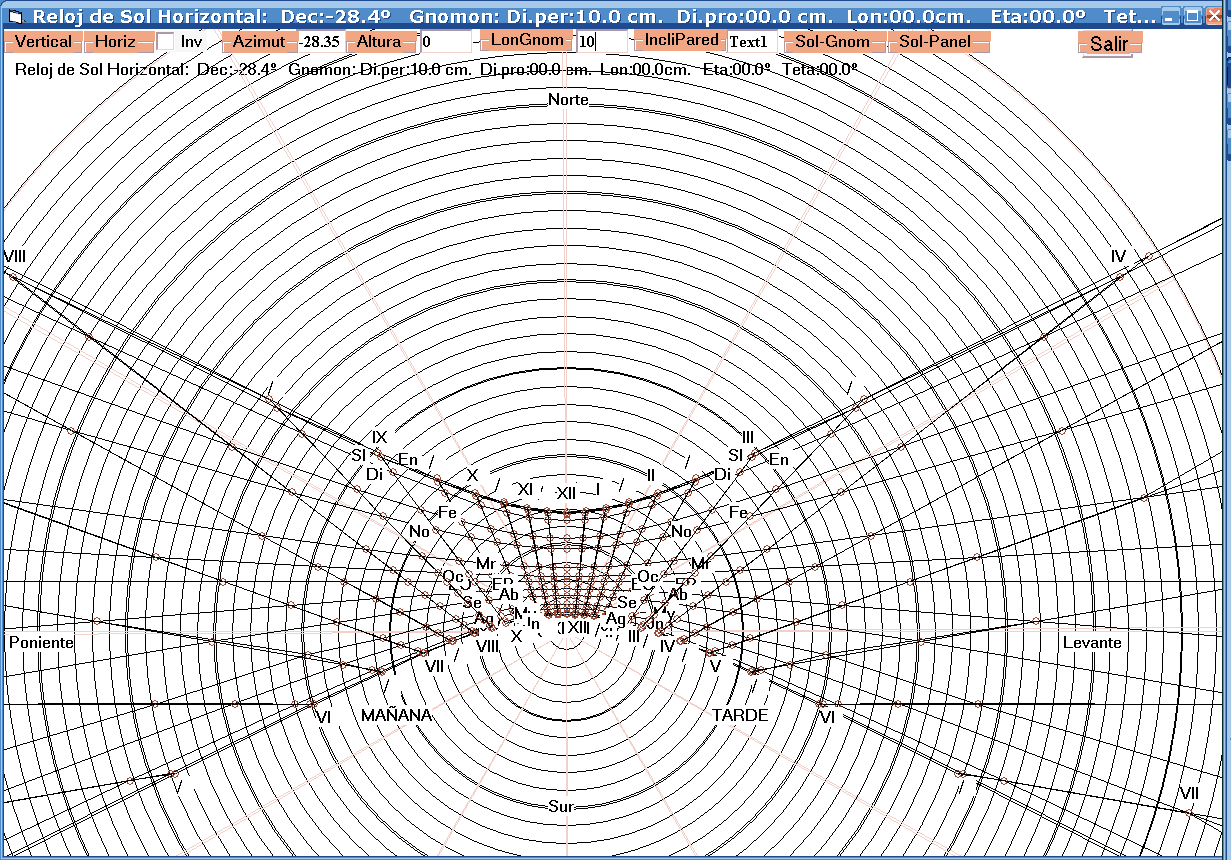
observamos mejor algunas características y propiedades interesantes del reloj, de su gráfico:

1. Todos las rectas horarias pasan por un punto.

2. Las correspondientes a las 12 (XII) son verticales y las de las seis (VI) horizontales ambas, mañana y tarde.

3. En consecuencia se cubren 90º en 6 horas, correspondiendo a a cada una (si los ángulos cada hora son iguales, lo que veremos enseguida) 15º, Las 24 horas se cubren claro esta en 360º, una vuelta completa que el sol (aparentemente) da, volviendo a su posición anterior el día siguiente. Se comporta como un reloj convencional de 24 horas, con una manecilla (una sombra) que gira regularmente y además señala el mes (y sus fracciones si la figura es suficientemente grande).

4. De modo que a 1 hora de tiempo le corresponden 15º, y a 1 minuto de tiempo la 60ava parte, es decir, 15 minutos de ángulo, un cuarto de grado.

5. No todas las horas se ven, solo las diurnas (reloj de sol) y de estas sólo aquellas en que el sol sobrepasa el horizonte y además ilumina al propio reloj (es decir, no hay árboles, edificios le que oculten el sol).

6. Esto ocurre en verano en más de 12 horas y el invierno en menos. Son exactamente 12 en los equinoccios

Primer refinamiento

Si aplicamos la corrección descrita en Analemma, encontramos una trayectorias de la sombra con esa forma aproximada.

y, si interpolamos, encontramos la analemma (curva en 8) proyectada en el reloj horizontal:

Nótense, en abanico, las líneas horarias centrales o neutras (sin corrección) y las figuras en forma de paleta con eje en las anteriores: la corrección está incluida en el dibujo, la parte izquierda los primeros meses del año, la derecha los últimos. La paletas se tocan, incluso se solapan, porque la corrección llega a 16 minutos y cada una corresponde a media hora

Segundo refinamiento

Podemos incluso interpolar entre cada cuadrícula correspondiente a los datos originales de mes y hora: es decir cualquier día se interpola entre los meses y cualquier hora se interpola entre los valores ya interpolados del día: (explicar) el resultado es más preciso (dentro de la aproximación inherente a toda interpolación, que es lineal)

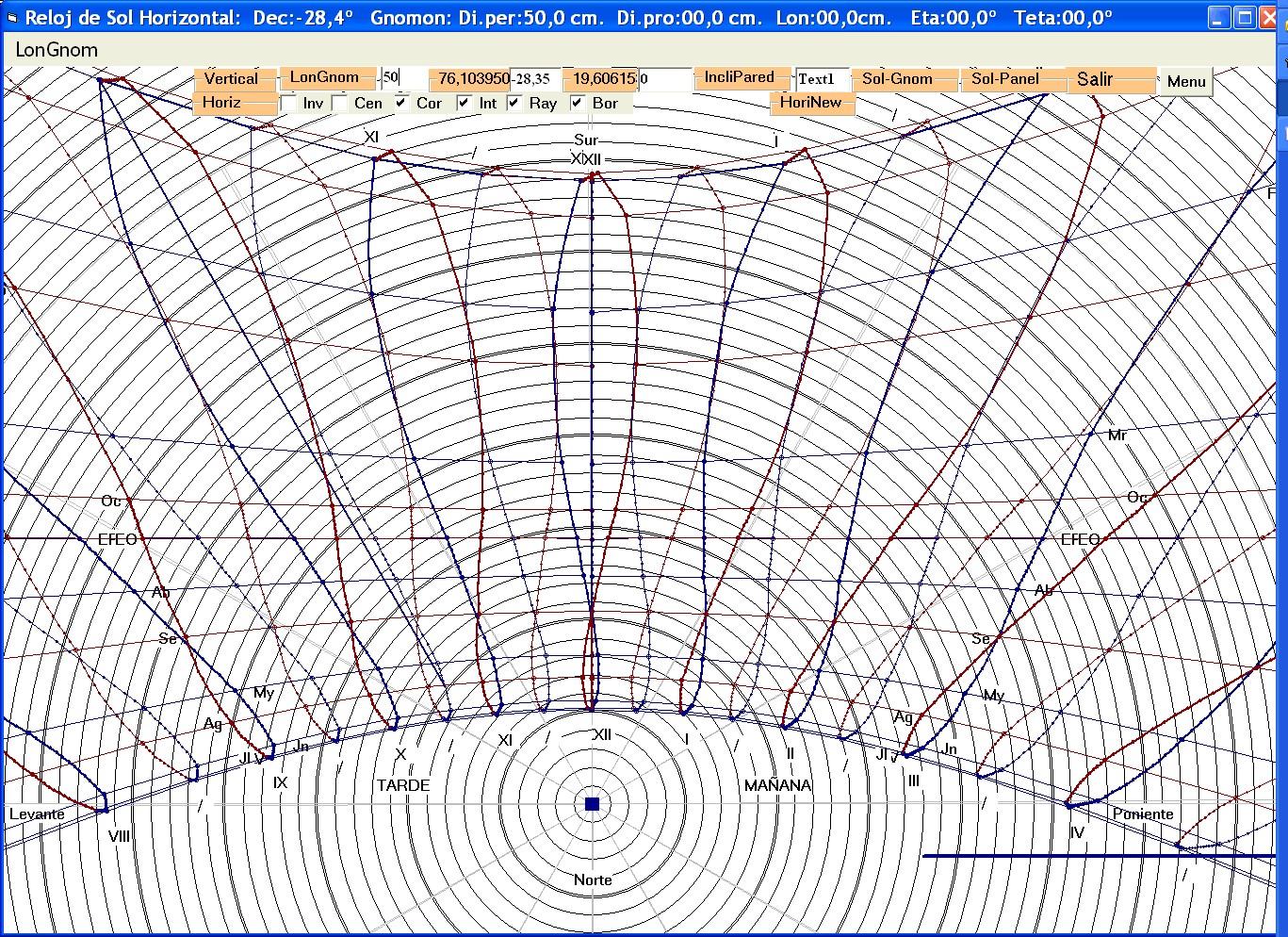
El refinamiento último consistirá en aplicar las ecuaciones de la posición del sol y la tierra en cualquier momento y lugar.

Vuelta al Principio Última actualización Tuesday, 30 de April de 2013 Visitantes: